Chào mừng các em học sinh đến với bài giải bài tập 7.6 trang 34 SGK Toán 9 tập 2 trên giaitoan.edu.vn. Bài tập này thuộc chương trình học Toán 9 tập 2, tập trung vào việc vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.
Một chiếc đồng hồ trong Hình 7.9 có đường viền là một đường tròn tiếp xúc với ba cạnh của khung đồng hồ hình tam giác đều. Đường kính của đường viền mặt đồng hồ là 10 cm. Khung hình tam giác đều của đồng hồ có độ dài cạnh là bao nhiêu centimet (độ dày đường viền của khung không đáng kể)? Làm tròn kết quả đến hàng phần mười.
Đề bài
Một chiếc đồng hồ trong Hình 7.9 có đường viền là một đường tròn tiếp xúc với ba cạnh của khung đồng hồ hình tam giác đều. Đường kính của đường viền mặt đồng hồ là 10 cm. Khung hình tam giác đều của đồng hồ có độ dài cạnh là bao nhiêu centimet (độ dày đường viền của khung không đáng kể)? Làm tròn kết quả đến hàng phần mười.

Phương pháp giải - Xem chi tiết
Đường tròn nội tiếp của tam giác đều cạnh a có tâm là trọng tâm tam giác đều.
Áp dụng hệ thức lượng trong tam giác vuông để tính cạnh của khung đồng hồ.
Lời giải chi tiết
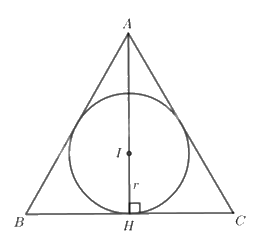
Ta có đường kính của đường viền mặt đồng hồ là 10 cm suy ra bán kính r = 5 cm.
Giả sử tam giác ABC đều có đường tròn nội tiếp tâm I bán kính r
Do đó, I nằm trên đường phân giác góc A.
Gọi H là trung điểm của BC
Mà tam giác ABC đều nên đường phân giác AI cũng là đường trung tuyến, do A, H, I thẳng hàng và AH là đường cao.
I là trọng tâm tam giác ABC nên ta có:
IH = \(\frac{1}{3}\)AH suy AH = 3IH = 3r
Xét tam giác AHB vuông tại H.
\(\widehat B = {60^o}\) (do tam giác ABC đều)
Áp dụng hệ thức lượng trong tam giác vuông ta có:
BH = AH. cot B = AH. cot 60o = 3r .\(\frac{{\sqrt 3 }}{3}\) = r.\(\sqrt 3 \)
Suy ra BC = 2BH = 2r\(\sqrt 3 \) = 2.5.\(\sqrt 3 \) = 10\(\sqrt 3 \approx 17,3cm\).
Bài tập 7.6 trang 34 SGK Toán 9 tập 2 yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết một bài toán thực tế liên quan đến việc xác định phương trình đường thẳng đi qua hai điểm cho trước. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các khái niệm và công thức sau:
Để giúp các em hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ cùng nhau phân tích từng bước thực hiện:
Giả sử đề bài yêu cầu tìm phương trình đường thẳng đi qua hai điểm A(1, 2) và B(3, 6). Chúng ta sẽ thực hiện các bước sau:
(y - 2) / (x - 1) = (6 - 2) / (3 - 1)
(y - 2) / (x - 1) = 4 / 2
(y - 2) / (x - 1) = 2
y - 2 = 2(x - 1)
y - 2 = 2x - 2
y = 2x
Ngoài bài tập 7.6 trang 34 SGK Toán 9 tập 2, còn rất nhiều bài tập tương tự yêu cầu học sinh vận dụng kiến thức về hàm số và phương trình đường thẳng. Để nâng cao kỹ năng giải toán, các em có thể thực hành thêm các bài tập sau:
Bài tập 7.6 trang 34 SGK Toán 9 tập 2 là một bài tập quan trọng giúp các em củng cố kiến thức về hàm số và phương trình đường thẳng. Hy vọng với lời giải chi tiết và ví dụ minh họa trên, các em sẽ hiểu rõ hơn về cách giải bài tập này và tự tin hơn trong các kỳ thi sắp tới. Chúc các em học tập tốt!