Giải bài tập 5.23 trang 121 SGK Toán 9 tập 1

Giải bài tập 5.23 trang 121 SGK Toán 9 tập 1 - Cùng khám phá

Giải bài tập 5.23 trang 121 SGK Toán 9 tập 1

Bài tập 5.23 trang 121 SGK Toán 9 tập 1 là một bài toán quan trọng trong chương trình học. Bài tập này giúp học sinh rèn luyện kỹ năng giải phương trình bậc hai và ứng dụng vào các bài toán thực tế.

Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu và các phương pháp giải khác nhau để giúp bạn hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự.

Cho điểm A thuộc đường tròn (O). Trên tiếp tuyến tại A của (O) xác định điểm M sao cho \(AM = AO\). Đường thẳng OM cắt (O) tại B và C (B nằm giữa O và M). a) Tính góc ở tâm BOA. b) Tính số đo cung lớn AC.

Đề bài

Cho điểm A thuộc đường tròn (O). Trên tiếp tuyến tại A của (O) xác định điểm M sao cho \(AM = AO\). Đường thẳng OM cắt (O) tại B và C (B nằm giữa O và M).

a) Tính góc ở tâm BOA.

b) Tính số đo cung lớn AC.

Phương pháp giải - Xem chi tiết Giải bài tập 5.23 trang 121 SGK Toán 9 tập 1 - Cùng khám phá 1

a) Chứng minh tam giác MOA vuông cân tại O, suy ra \(\widehat {BOA} = {45^o}\).

b) Tính số đo góc AOC, từ đó tính số đo cung AC nhỏ, từ đó tính được số đo cung AC lớn.

Lời giải chi tiết

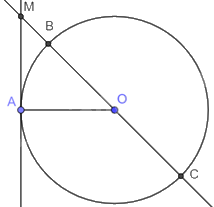
Giải bài tập 5.23 trang 121 SGK Toán 9 tập 1 - Cùng khám phá 2

a) Vì MA là tiếp tuyến của (O) nên \(MA \bot AO\), suy ra tam giác AMO vuông tại A. Mà \(MA = OA\) nên tam giác AMO vuông cân tại O. Do đó, \(\widehat {BOA} = {45^o}\).

b) Ta có: \(\widehat {AOC} = {180^o} - \widehat {BOA} = {135^o}\)

Vì AOC là góc ở tâm chắn cung nhỏ AC nên \(sđ\overset\frown{A{{C}_{nhỏ}}}={{135}^{o}}\).

Số đo cung AC lớn là: \({360^o} - {135^o} = {225^o}\).

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài tập 5.23 trang 121 SGK Toán 9 tập 1 - Cùng khám phá đặc sắc thuộc chuyên mục giải toán 9 trên nền tảng toán học. Với bộ bài tập toán thcs được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài tập 5.23 trang 121 SGK Toán 9 tập 1: Phương pháp giải và ứng dụng

Bài tập 5.23 trang 121 SGK Toán 9 tập 1 thuộc chương trình đại số, cụ thể là phần phương trình bậc hai một ẩn. Bài toán này yêu cầu học sinh vận dụng kiến thức về công thức nghiệm của phương trình bậc hai để tìm ra nghiệm của phương trình, đồng thời kiểm tra lại nghiệm để đảm bảo tính chính xác.

Nội dung bài tập 5.23 trang 121 SGK Toán 9 tập 1

Bài tập thường có dạng: Giải phương trình sau: ax² + bx + c = 0, với a, b, c là các hệ số cho trước.

Phương pháp giải bài tập 5.23 trang 121 SGK Toán 9 tập 1

Xác định hệ số a, b, c: Đầu tiên, cần xác định chính xác các hệ số a, b, c của phương trình bậc hai.
Tính delta (Δ): Tính delta theo công thức Δ = b² - 4ac.
Xét các trường hợp của delta:
- Nếu Δ > 0: Phương trình có hai nghiệm phân biệt: x₁ = (-b + √Δ) / 2a và x₂ = (-b - √Δ) / 2a.
- Nếu Δ = 0: Phương trình có nghiệm kép: x₁ = x₂ = -b / 2a.
- Nếu Δ < 0: Phương trình vô nghiệm.
Kiểm tra nghiệm: Thay các nghiệm tìm được vào phương trình ban đầu để kiểm tra tính đúng đắn.

Ví dụ minh họa giải bài tập 5.23 trang 121 SGK Toán 9 tập 1

Ví dụ: Giải phương trình 2x² - 5x + 2 = 0

a = 2, b = -5, c = 2
Δ = (-5)² - 4 * 2 * 2 = 25 - 16 = 9
Δ > 0, phương trình có hai nghiệm phân biệt:
- x₁ = (5 + √9) / (2 * 2) = (5 + 3) / 4 = 2
- x₂ = (5 - √9) / (2 * 2) = (5 - 3) / 4 = 0.5
Kiểm tra:
- Thay x = 2 vào phương trình: 2 * 2² - 5 * 2 + 2 = 8 - 10 + 2 = 0 (đúng)
- Thay x = 0.5 vào phương trình: 2 * (0.5)² - 5 * 0.5 + 2 = 0.5 - 2.5 + 2 = 0 (đúng)

Vậy phương trình 2x² - 5x + 2 = 0 có hai nghiệm là x₁ = 2 và x₂ = 0.5.