Chào mừng các em học sinh đến với bài giải bài tập 5.36 trang 127 SGK Toán 9 tập 1 trên giaitoan.edu.vn. Bài tập này thuộc chương Hàm số bậc nhất và ứng dụng. Chúng tôi sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.
Giaitoan.edu.vn là nền tảng học toán online uy tín, cung cấp đầy đủ các bài giải SGK, bài tập nâng cao và các tài liệu học tập hữu ích khác.
Cho hai đường tròn tâm O và I cắt nhau tại M và N. Vẽ một đường thẳng qua M cắt (O) tại A và cắt (I) tại B, một đường thẳng qua N cắt (O) tại C và (I) tại D. Chứng minh rằng AC//BD.
Đề bài
Cho hai đường tròn tâm O và I cắt nhau tại M và N. Vẽ một đường thẳng qua M cắt (O) tại A và cắt (I) tại B, một đường thẳng qua N cắt (O) tại C và (I) tại D. Chứng minh rằng AC//BD.
Phương pháp giải - Xem chi tiết
+ Chứng minh \(\widehat {NMB} + \widehat {NDB}\)$=\frac{1}{2}\left( sđ\overset\frown{NDB}+sđ\overset\frown{NMB} \right)$\( = \frac{1}{2}{.360^o}\)\( = {180^o}\).
+ Chứng minh \(\widehat {ACN} + \widehat {AMN} = {180^o}\), \(\widehat {NMB} + \widehat {AMN} = {180^o}\) nên \(\widehat {ACN} = \widehat {NMB}\)
+ Do đó, \(\widehat {ACN} + \widehat {NDB} = {180^o}\).
+ Gọi E là giao điểm của AB và CD.
Do đó: \(\widehat {BDE} + \widehat {NDB} = {180^o}\).
Suy ra \(\widehat {ACN} = \widehat {BDE}\) nên AC//BD.
Lời giải chi tiết
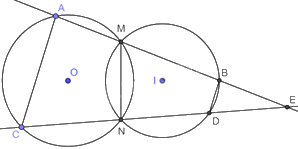
Xét (I): Vì NMB là góc nội tiếp chắn cung NDB nên $\widehat{NMB}=\frac{1}{2}sđ\overset\frown{NDB}$.
Vì NDB là góc nội tiếp chắn cung NMB nên $\widehat{NDB}=\frac{1}{2}sđ\overset\frown{NMB}$.
Do đó, \(\widehat {NMB} + \widehat {NDB}\)$=\frac{1}{2}\left( sđ\overset\frown{NDB}+sđ\overset\frown{NMB} \right)$\( = \frac{1}{2}{.360^o}\)\( = {180^o}\)(1)
Chứng minh tương tự ta có: \(\widehat {ACN} + \widehat {AMN} = {180^o}\).
Mà \(\widehat {NMB} + \widehat {AMN} = {180^o}\) nên \(\widehat {ACN} = \widehat {NMB}\) (2)
Từ (1) và (2) ta có: \(\widehat {ACN} + \widehat {NDB} = {180^o}\).
Gọi E là giao điểm của AB và CD.
Do đó: \(\widehat {BDE} + \widehat {NDB} = {180^o}\)
Suy ra \(\widehat {ACN} = \widehat {BDE}\), mà hai góc này ở vị trí đồng vị.
Do đó, AC//BD.
Bài tập 5.36 trang 127 SGK Toán 9 tập 1 yêu cầu chúng ta tìm hiểu về phương pháp tiếp tuyến của đồ thị hàm số bậc nhất. Đây là một kiến thức quan trọng trong chương trình Toán 9, giúp học sinh hiểu rõ hơn về mối quan hệ giữa hàm số và đồ thị của nó.
Bài tập 5.36 thường có dạng như sau: Cho hàm số y = ax + b. Tìm hệ số a và b sao cho đồ thị của hàm số tiếp xúc với đường thẳng d: y = cx + d tại một điểm cho trước.
Để giải bài tập này, chúng ta cần thực hiện các bước sau:
Bài toán: Cho hàm số y = 2x + 1. Tìm hệ số a và b sao cho đồ thị của hàm số tiếp xúc với đường thẳng d: y = -x + 4.
Giải:
Ngoài bài tập 5.36, còn có nhiều bài tập tương tự yêu cầu học sinh vận dụng kiến thức về phương pháp tiếp tuyến để giải quyết. Các bài tập này thường có dạng:
Khi giải bài tập 5.36, học sinh cần lưu ý những điều sau:
Bài tập 5.36 trang 127 SGK Toán 9 tập 1 là một bài tập quan trọng, giúp học sinh hiểu rõ hơn về phương pháp tiếp tuyến và ứng dụng của nó. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em học sinh sẽ nắm vững kiến thức và kỹ năng giải bài tập này.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!