Chào mừng các em học sinh đến với bài giải bài tập 5.22 trang 121 SGK Toán 9 tập 1 trên giaitoan.edu.vn. Bài tập này thuộc chương Hàm số bậc nhất và ứng dụng. Chúng tôi sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Giaitoan.edu.vn là nền tảng học toán online uy tín, cung cấp đầy đủ các bài giải SGK Toán 9, bài tập trắc nghiệm, và các tài liệu học tập hữu ích khác.
Vẽ đường tròn (O), sau đó vẽ: a) Một góc ở tâm của (O) có số đo \({50^o}\); b) Một cung có số đo \({235^o}\).
Đề bài
Vẽ đường tròn (O), sau đó vẽ:
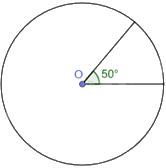
a) Một góc ở tâm của (O) có số đo \({50^o}\);
b) Một cung có số đo \({235^o}\).
Phương pháp giải - Xem chi tiết
a) Vẽ đường tròn tâm (O), vẽ một góc có đỉnh là tâm O bằng 50 độ, hai cạnh của góc O là hai bán kính của (O).
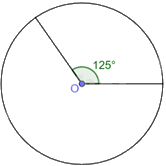
b) Vẽ đường tròn (O), vẽ một góc ở tâm có số đo bằng 125 độ. Khi đó, số đo cung nhỏ bị chặn bởi góc ở tâm đó bằng 125 độ và số đo cung lớn bằng 235 độ.
Lời giải chi tiết
a) Vẽ đường tròn tâm (O), vẽ một góc có đỉnh là tâm O bằng 50 độ, hai cạnh của góc O là hai bán kính của (O).
b) Vẽ đường tròn (O), vẽ một góc ở tâm có số đo bằng 125 độ. Khi đó, số đo cung nhỏ bị chặn bởi góc ở tâm đó bằng 125 độ và số đo cung lớn bằng 235 độ.
Bài tập 5.22 trang 121 SGK Toán 9 tập 1 yêu cầu chúng ta tìm hiểu về phương pháp tiếp tuyến của đồ thị hàm số bậc nhất. Đây là một kiến thức quan trọng trong chương trình Toán 9, giúp học sinh hiểu rõ hơn về mối quan hệ giữa hàm số và đồ thị của nó.
Bài tập 5.22 thường có dạng như sau: Cho hàm số y = ax + b. Tìm giá trị của a và b sao cho đồ thị của hàm số tiếp xúc với đường thẳng d: y = cx + d tại một điểm cho trước.
Để giải bài tập này, chúng ta cần thực hiện các bước sau:
Bài tập: Cho hàm số y = 2x + 1. Tìm giá trị của m sao cho đồ thị của hàm số y = 2x + 1 tiếp xúc với đường thẳng d: y = mx + 3.
Giải:
Để đồ thị hàm số y = 2x + 1 tiếp xúc với đường thẳng d: y = mx + 3, phương trình 2x + 1 = mx + 3 phải có nghiệm duy nhất.
Ta có: 2x + 1 = mx + 3 ⇔ (2 - m)x = 2.
Để phương trình có nghiệm duy nhất, ta cần 2 - m ≠ 0 ⇔ m ≠ 2.
Khi đó, x = 2 / (2 - m).
Thay x = 2 / (2 - m) vào y = 2x + 1, ta được: y = 2 * (2 / (2 - m)) + 1 = (4 + 2 - m) / (2 - m) = (6 - m) / (2 - m).
Thay x = 2 / (2 - m) và y = (6 - m) / (2 - m) vào y = mx + 3, ta được:
(6 - m) / (2 - m) = m * (2 / (2 - m)) + 3 ⇔ 6 - m = 2m + 3(2 - m) ⇔ 6 - m = 2m + 6 - 3m ⇔ 6 - m = 6 - m.
Phương trình này luôn đúng với mọi m ≠ 2.
Vậy, với mọi m ≠ 2, đồ thị của hàm số y = 2x + 1 tiếp xúc với đường thẳng d: y = mx + 3.
Để luyện tập thêm, các em có thể giải các bài tập tương tự sau:
Bài tập 5.22 trang 121 SGK Toán 9 tập 1 là một bài tập quan trọng, giúp học sinh hiểu rõ hơn về phương pháp tiếp tuyến của đồ thị hàm số bậc nhất. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em sẽ nắm vững kiến thức và tự tin giải các bài tập tương tự.