Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Trong bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho mục 2 trang 79, 80 SGK Toán 9 tập 2. Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Bạn An dùng một sợi dây dù dài và mỏng cuốn quanh một quả bóng đến khi bọc kín quả bóng đó bằng các vòng cuốn sát nhau và không chồng lên nhau (Hình 9.39). Bạn An cắt sợi dây dù tại điểm kết thúc quá trình cuốn dây quanh quả bóng, rồi lấy đoạn dây này cuốn từng vòng sát nhau quanh hộp hình trụ đựng quả bóng đó (Hình 9.40). Bạn An thấy rằng đoạn dây cuốn quanh hộp đựng bóng tạo thành một hình trụ có đường kính và chiều cao cùng bằng đường kính quả bóng. a) So sánh diện tích bề mặt quả bóng v
Trả lời câu hỏi Vận dụng 2 trang 80 SGK Toán 9 Cùng khám phá
Đại dương bao phủ khoảng 71% bề mặt Trái Đất. Hãy ước tính diện tích của đại dương theo kilomet vuông, biết bán kính Trái Đất khoảng 6371 km (làm tròn kết quả đến hàng triệu).
Phương pháp giải:
Diện tích mặt cầu là: \(S = 4\pi {R^2} = \pi {d^2}\) (R là bán kính và d là đường kính của mặt cầu)
Lời giải chi tiết:
Diện tích Trái Đất là:
\(S = 4\pi {R^2} = 4\pi .{\left( {6371} \right)^2} = 510\)(trệu km2)
Đại dương bao phủ khoảng 71% bề mặt Trái Đất nên diện tích đại dương khoảng: 510.71% = 362 triệu km2.
Trả lời câu hỏi Luyện tập 2 trang 80SGK Toán 9 Cùng khám phá
Một mặt cầu có diện tích là 36 cm2. Hỏi đường kính của mặt cầu này là bao nhiêu centimet (làm tròn kết quả đến hàng phần trăm)?
Phương pháp giải:
Diện tích mặt cầu là: \(S = 4\pi {R^2} = \pi {d^2}\) (R là bán kính và d là đường kính của mặt cầu)
Lời giải chi tiết:
Ta có \(S = \pi {d^2} = 36\)
Suy ra \(d = \sqrt {\frac{{36}}{\pi }} \approx 3,39\)cm.
Trả lời câu hỏi Hoạt động 3 trang 79SGK Toán 9 Cùng khám phá
Bạn An dùng một sợi dây dù dài và mỏng cuốn quanh một quả bóng đến khi bọc kín quả bóng đó bằng các vòng cuốn sát nhau và không chồng lên nhau (Hình 9.39).

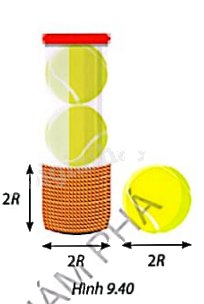
Bạn An cắt sợi dây dù tại điểm kết thúc quá trình cuốn dây quanh quả bóng, rồi lấy đoạn dây này cuốn từng vòng sát nhau quanh hộp hình trụ đựng quả bóng đó (Hình 9.40). Bạn An thấy rằng đoạn dây cuốn quanh hộp đựng bóng tạo thành một hình trụ có đường kính và chiều cao cùng bằng đường kính quả bóng.
a) So sánh diện tích bề mặt quả bóng với phần diện tích của hộp đựng bị quấn bởi sợi dây dù.
b) Gọi R là bán kính của quả bóng. Viết công thức tính diện tích xung quanh của hình trụ do đoạn dây cuốn quanh hộp đựng bóng tạo thành theo R, từ đó suy ra diện tích bề mặt của quả bóng.
Phương pháp giải:
Nhìn hình và nhận xét.
Lời giải chi tiết:
a) Diện tích bề mặt quả bóng bằng với diện tích xung quanh của hộp đựng.
b) Diện tích xung quanh của hộp đựng là:
\(S = 2\pi .R.2R = 4\pi {R^2}\)
Diện tích bề mặt quả bóng là:
\(S = 4\pi {R^2}\).
Trả lời câu hỏi Hoạt động 3 trang 79SGK Toán 9 Cùng khám phá
Bạn An dùng một sợi dây dù dài và mỏng cuốn quanh một quả bóng đến khi bọc kín quả bóng đó bằng các vòng cuốn sát nhau và không chồng lên nhau (Hình 9.39).

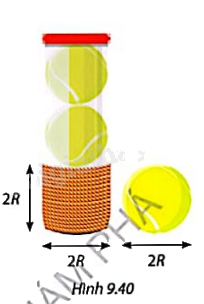
Bạn An cắt sợi dây dù tại điểm kết thúc quá trình cuốn dây quanh quả bóng, rồi lấy đoạn dây này cuốn từng vòng sát nhau quanh hộp hình trụ đựng quả bóng đó (Hình 9.40). Bạn An thấy rằng đoạn dây cuốn quanh hộp đựng bóng tạo thành một hình trụ có đường kính và chiều cao cùng bằng đường kính quả bóng.
a) So sánh diện tích bề mặt quả bóng với phần diện tích của hộp đựng bị quấn bởi sợi dây dù.
b) Gọi R là bán kính của quả bóng. Viết công thức tính diện tích xung quanh của hình trụ do đoạn dây cuốn quanh hộp đựng bóng tạo thành theo R, từ đó suy ra diện tích bề mặt của quả bóng.
Phương pháp giải:
Nhìn hình và nhận xét.
Lời giải chi tiết:
a) Diện tích bề mặt quả bóng bằng với diện tích xung quanh của hộp đựng.
b) Diện tích xung quanh của hộp đựng là:
\(S = 2\pi .R.2R = 4\pi {R^2}\)
Diện tích bề mặt quả bóng là:
\(S = 4\pi {R^2}\).
Trả lời câu hỏi Luyện tập 2 trang 80SGK Toán 9 Cùng khám phá
Một mặt cầu có diện tích là 36 cm2. Hỏi đường kính của mặt cầu này là bao nhiêu centimet (làm tròn kết quả đến hàng phần trăm)?
Phương pháp giải:
Diện tích mặt cầu là: \(S = 4\pi {R^2} = \pi {d^2}\) (R là bán kính và d là đường kính của mặt cầu)
Lời giải chi tiết:
Ta có \(S = \pi {d^2} = 36\)
Suy ra \(d = \sqrt {\frac{{36}}{\pi }} \approx 3,39\)cm.
Trả lời câu hỏi Vận dụng 2 trang 80 SGK Toán 9 Cùng khám phá
Đại dương bao phủ khoảng 71% bề mặt Trái Đất. Hãy ước tính diện tích của đại dương theo kilomet vuông, biết bán kính Trái Đất khoảng 6371 km (làm tròn kết quả đến hàng triệu).
Phương pháp giải:
Diện tích mặt cầu là: \(S = 4\pi {R^2} = \pi {d^2}\) (R là bán kính và d là đường kính của mặt cầu)
Lời giải chi tiết:
Diện tích Trái Đất là:
\(S = 4\pi {R^2} = 4\pi .{\left( {6371} \right)^2} = 510\)(trệu km2)
Đại dương bao phủ khoảng 71% bề mặt Trái Đất nên diện tích đại dương khoảng: 510.71% = 362 triệu km2.
Mục 2 trang 79, 80 SGK Toán 9 tập 2 thường xoay quanh các chủ đề về hàm số bậc nhất, hàm số bậc hai, và các ứng dụng của chúng. Các bài tập trong mục này yêu cầu học sinh vận dụng kiến thức về định nghĩa, tính chất, đồ thị của hàm số để giải quyết các bài toán thực tế. Việc nắm vững kiến thức nền tảng và kỹ năng giải toán là vô cùng quan trọng để hoàn thành tốt các bài tập này.
Chúng ta sẽ đi vào giải chi tiết từng bài tập trong mục 2 trang 79, 80 SGK Toán 9 tập 2. Lưu ý rằng, trước khi bắt đầu giải bài tập, các em nên đọc kỹ đề bài, xác định rõ yêu cầu và các dữ kiện đã cho. Sau đó, các em có thể áp dụng các công thức, định lý và phương pháp giải toán phù hợp để tìm ra đáp án chính xác.
Bài tập này yêu cầu học sinh xác định hệ số a của hàm số bậc nhất dựa vào các thông tin đã cho, chẳng hạn như đồ thị của hàm số hoặc các điểm thuộc đồ thị. Để giải bài tập này, các em có thể sử dụng công thức tính hệ số góc của đường thẳng hoặc phương pháp thay tọa độ điểm vào phương trình hàm số.
Bài tập này yêu cầu học sinh vẽ đồ thị của hàm số bậc nhất. Để vẽ đồ thị, các em cần xác định ít nhất hai điểm thuộc đồ thị, sau đó nối chúng lại bằng một đường thẳng. Lưu ý rằng, đồ thị của hàm số bậc nhất là một đường thẳng.
Bài tập này yêu cầu học sinh tìm giao điểm của hai đường thẳng. Để tìm giao điểm, các em có thể giải hệ phương trình bậc nhất hai ẩn tương ứng với hai đường thẳng. Giao điểm của hai đường thẳng là nghiệm của hệ phương trình.
Bài tập này yêu cầu học sinh ứng dụng kiến thức về hàm số bậc nhất vào giải quyết các bài toán thực tế, chẳng hạn như bài toán về quãng đường, vận tốc, thời gian. Để giải bài tập này, các em cần phân tích đề bài, xác định mối quan hệ giữa các đại lượng và xây dựng phương trình hàm số phù hợp.
Để giải các bài tập trong mục 2 trang 79, 80 SGK Toán 9 tập 2 một cách hiệu quả, các em có thể áp dụng một số phương pháp sau:
Để nắm vững kiến thức và kỹ năng giải toán, các em nên luyện tập thường xuyên với các bài tập khác nhau. Các em có thể tìm các bài tập trong SGK, sách bài tập, hoặc trên các trang web học toán online như giaitoan.edu.vn. Việc luyện tập thường xuyên sẽ giúp các em tự tin hơn khi làm bài kiểm tra và thi cử.
Hy vọng rằng, với lời giải chi tiết và phương pháp giải toán hiệu quả mà chúng tôi đã cung cấp, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 2 trang 79, 80 SGK Toán 9 tập 2. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!
| Bài tập | Nội dung chính |
|---|---|
| Bài 1 | Xác định hệ số a của hàm số bậc nhất |
| Bài 2 | Vẽ đồ thị hàm số bậc nhất |
| Bài 3 | Tìm giao điểm của hai đường thẳng |
| Bài 4 | Ứng dụng hàm số bậc nhất vào bài toán thực tế |