Chào mừng các em học sinh đến với bài giải bài tập 6.37 trang 24 SGK Toán 9 tập 2 tại giaitoan.edu.vn. Bài tập này thuộc chương hàm số bậc nhất và ứng dụng, một trong những chủ đề quan trọng của chương trình Toán 9.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.
Hình 6.11 là đồ thị hàm số y = f(x) = ax2 (a\( \ne \)0). Gí trị của a bằng A. 3 B. \(\frac{1}{3}\) C. 1 D. \(\frac{1}{2}\)
Đề bài
Hình 6.11 là đồ thị hàm số y = f(x) = ax2 (a\( \ne \)0). Gí trị của a bằng
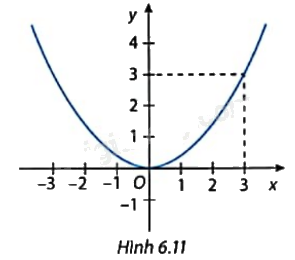
A. 3
B. \(\frac{1}{3}\)
C. 1
D. \(\frac{1}{2}\)
Phương pháp giải - Xem chi tiết
Lấy một điểm thuộc đồ thị A(3;3) thay vào y = f(x) = ax2 (a\( \ne \)0) để tìm a.
Lời giải chi tiết
Điểm A(3;3) thuộc đồ thị như hình.
Thay x = 3; y = 3 vào y = ax2 ta có: 3 = a.32
Suy ra a = \(\frac{1}{3}\).
Chọn đáp án B.
Bài tập 6.37 trang 24 SGK Toán 9 tập 2 yêu cầu học sinh vận dụng kiến thức về phương pháp tiếp tuyến để giải quyết một bài toán thực tế. Bài toán thường liên quan đến việc xác định phương trình tiếp tuyến của một đường cong tại một điểm cho trước, hoặc tìm điểm tiếp xúc khi biết phương trình tiếp tuyến.
Để giải bài tập này, các em cần thực hiện các bước sau:
Giả sử bài toán yêu cầu tìm phương trình tiếp tuyến của đường cong y = x2 tại điểm M(1; 1). Ta thực hiện như sau:
Ngoài bài tập 6.37, các em có thể gặp các dạng bài tập tương tự như:
Đối với các bài tập này, các em cần nắm vững lý thuyết, thực hành giải nhiều bài tập khác nhau và rèn luyện kỹ năng tư duy logic.
Bài tập 6.37 trang 24 SGK Toán 9 tập 2 là một bài tập quan trọng giúp các em củng cố kiến thức về phương pháp tiếp tuyến và ứng dụng. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa trên, các em sẽ tự tin giải quyết bài tập này và các bài tập tương tự một cách hiệu quả.
Hãy luyện tập thường xuyên và đừng ngần ngại tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè nếu gặp khó khăn. Chúc các em học tập tốt!
| Khái niệm | Giải thích |
|---|---|
| Tiếp tuyến | Đường thẳng chỉ tiếp xúc với đường cong tại một điểm. |
| Hệ số góc | Độ dốc của đường thẳng. |
| Đạo hàm | Công cụ để tính hệ số góc của tiếp tuyến. |
| Bảng tóm tắt các khái niệm quan trọng. | |