Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 1 trang 37 và 38 sách giáo khoa Toán 9 tập 1.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài toán, nắm vững phương pháp giải và tự tin làm bài tập.
Chủ đầu tư khu chung cư Vạn Xuân muốn quy hoạch khu đất hình chữ nhật kích thước \(50m \times 75m\) giữa các tòa nhà bằng cách chia nó thành ba hình chữ nhật nhỏ A, B, C như Hình 2.3. Phần A dùng để làm sân tập luyện thể thao (có thể chơi bóng rổ, bóng chuyền), phần B dành để trồng cây xanh và phần C là nơi đặt cầu trượt, bập bênh cho trẻ em. Chủ đầu tư muốn chia khu đất sao cho diện tích hình A không nhỏ hơn diện tích hình B. Xét bản thiết kế của chủ đầu tư khu chung cư Vạn Xuân. a) Viết biể
Trả lời câu hỏi Luyện tập 1 trang 38 SGK Toán 9 Cùng khám phá
Cho một ví dụ về bất phương trình ẩn \(u\). Chỉ rõ vế trái và vế phải của bất phương trình đó.
Phương pháp giải:
Dựa vào định nghĩa bất phương trình để đưa ví dụ.
Lời giải chi tiết:
Ví dụ về bất phương trình ẩn \(u\): \(u \ge 2{u^2} - 1\).
Vế trái của bất phương trình là \(u\).
Vế phải của bất phương trình là \(2{u^2} - 1\).
Trả lời câu hỏi Hoạt động 2 trang 38 SGK Toán 9 Cùng khám phá
Cho bất phương trình \({x^2} < 2x + 3\).
a) Khi thay \(x = 1\) vào hai vế của bất phương trình, ta được một khẳng định đúng hay sai?
b) Khi thay \(x = 5\) vào hai vế của bất phương trình, ta được một khẳng định đúng hay sai?
Phương pháp giải:
Thay số vào hai vế của bất phương trình để giải bài toán.
Lời giải chi tiết:
a) Thay \(x = 1\) vào hai vế của bất phương trình \({x^2} < 2x + 3\), ta có: \(1 < 5\).
Đây là một khẳng định đúng.
b) Thay \(x = 5\) vào hai vế của bất phương trình \({x^2} < 2x + 3\), ta có: \(25 < 13\).
Đây là một khẳng định sai.
Trả lời câu hỏi Luyện tập 2 trang 38 SGK Toán 9 Cùng khám phá
\(x = - 2\) là một nghiệm của bất phương trình nào trong các bất phương trình sau?
a) \(x\left( {x - 1} \right) < x + 2\);
b) \({x^2} - 2 > 0\).
Phương pháp giải:
Thay số vào bất phương trình để giải bài toán.
Lời giải chi tiết:
a) Thay \(x = - 2\) vào hai vế của bất phương trình \(x\left( {x - 1} \right) < x + 2\), ta có: \(6 < 0\).
Đây là một khẳng định sai.
Vậy \(x = - 2\) không phải là một nghiệm của bất phương trình.
b) Thay \(x = - 2\) vào hai vế của bất phương trình \({x^2} - 2 > 0\), ta có: \(2 > 0\).
Đây là một khẳng định đúng.
Vậy \(x = - 2\) là một nghiệm của bất phương trình.
Trả lời câu hỏi Hoạt động 1 trang 37 SGK Toán 9 Cùng khám phá
Chủ đầu tư khu chung cư Vạn Xuân muốn quy hoạch khu đất hình chữ nhật kích thước \(50m \times 75m\) giữa các tòa nhà bằng cách chia nó thành ba hình chữ nhật nhỏ A, B, C như Hình 2.3. Phần A dùng để làm sân tập luyện thể thao (có thể chơi bóng rổ, bóng chuyền), phần B dành để trồng cây xanh và phần C là nơi đặt cầu trượt, bập bênh cho trẻ em. Chủ đầu tư muốn chia khu đất sao cho diện tích hình A không nhỏ hơn diện tích hình B.
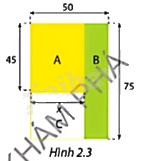
Xét bản thiết kế của chủ đầu tư khu chung cư Vạn Xuân.
a) Viết biểu thức tính diện tích hình chữ nhật A và biểu thức tính diện tích hình chữ nhật B.
b) Viết điện kiện mà số dương \(x\) cần thỏa mãn để diện tích hình A không nhỏ hơn diện tích hình B.
Phương pháp giải:
Dựa vào bất đẳng thức để giải bài toán.
Lời giải chi tiết:
a) Biểu thức tính diện tích hình chữ nhật A là: \(45x\left( {{m^2}} \right)\).
Biểu thức tính diện tích hình chữ nhật B là: \(75.\left( {50 - x} \right)\,\,\left( {{m^2}} \right)\).
b) Điều kiện mà số dương \(x\) cần thỏa mãn để diện tích hình A không nhỏ hơn diện tích hình B là: \(45x \ge 75.\left( {50 - x} \right)\).
Trả lời câu hỏi Hoạt động 1 trang 37 SGK Toán 9 Cùng khám phá
Chủ đầu tư khu chung cư Vạn Xuân muốn quy hoạch khu đất hình chữ nhật kích thước \(50m \times 75m\) giữa các tòa nhà bằng cách chia nó thành ba hình chữ nhật nhỏ A, B, C như Hình 2.3. Phần A dùng để làm sân tập luyện thể thao (có thể chơi bóng rổ, bóng chuyền), phần B dành để trồng cây xanh và phần C là nơi đặt cầu trượt, bập bênh cho trẻ em. Chủ đầu tư muốn chia khu đất sao cho diện tích hình A không nhỏ hơn diện tích hình B.
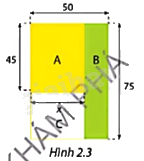
Xét bản thiết kế của chủ đầu tư khu chung cư Vạn Xuân.
a) Viết biểu thức tính diện tích hình chữ nhật A và biểu thức tính diện tích hình chữ nhật B.
b) Viết điện kiện mà số dương \(x\) cần thỏa mãn để diện tích hình A không nhỏ hơn diện tích hình B.
Phương pháp giải:
Dựa vào bất đẳng thức để giải bài toán.
Lời giải chi tiết:
a) Biểu thức tính diện tích hình chữ nhật A là: \(45x\left( {{m^2}} \right)\).
Biểu thức tính diện tích hình chữ nhật B là: \(75.\left( {50 - x} \right)\,\,\left( {{m^2}} \right)\).
b) Điều kiện mà số dương \(x\) cần thỏa mãn để diện tích hình A không nhỏ hơn diện tích hình B là: \(45x \ge 75.\left( {50 - x} \right)\).
Trả lời câu hỏi Luyện tập 1 trang 38 SGK Toán 9 Cùng khám phá
Cho một ví dụ về bất phương trình ẩn \(u\). Chỉ rõ vế trái và vế phải của bất phương trình đó.
Phương pháp giải:
Dựa vào định nghĩa bất phương trình để đưa ví dụ.
Lời giải chi tiết:
Ví dụ về bất phương trình ẩn \(u\): \(u \ge 2{u^2} - 1\).
Vế trái của bất phương trình là \(u\).
Vế phải của bất phương trình là \(2{u^2} - 1\).
Trả lời câu hỏi Hoạt động 2 trang 38 SGK Toán 9 Cùng khám phá
Cho bất phương trình \({x^2} < 2x + 3\).
a) Khi thay \(x = 1\) vào hai vế của bất phương trình, ta được một khẳng định đúng hay sai?
b) Khi thay \(x = 5\) vào hai vế của bất phương trình, ta được một khẳng định đúng hay sai?
Phương pháp giải:
Thay số vào hai vế của bất phương trình để giải bài toán.
Lời giải chi tiết:
a) Thay \(x = 1\) vào hai vế của bất phương trình \({x^2} < 2x + 3\), ta có: \(1 < 5\).
Đây là một khẳng định đúng.
b) Thay \(x = 5\) vào hai vế của bất phương trình \({x^2} < 2x + 3\), ta có: \(25 < 13\).
Đây là một khẳng định sai.
Trả lời câu hỏi Luyện tập 2 trang 38 SGK Toán 9 Cùng khám phá
\(x = - 2\) là một nghiệm của bất phương trình nào trong các bất phương trình sau?
a) \(x\left( {x - 1} \right) < x + 2\);
b) \({x^2} - 2 > 0\).
Phương pháp giải:
Thay số vào bất phương trình để giải bài toán.
Lời giải chi tiết:
a) Thay \(x = - 2\) vào hai vế của bất phương trình \(x\left( {x - 1} \right) < x + 2\), ta có: \(6 < 0\).
Đây là một khẳng định sai.
Vậy \(x = - 2\) không phải là một nghiệm của bất phương trình.
b) Thay \(x = - 2\) vào hai vế của bất phương trình \({x^2} - 2 > 0\), ta có: \(2 > 0\).
Đây là một khẳng định đúng.
Vậy \(x = - 2\) là một nghiệm của bất phương trình.
Mục 1 của chương trình Toán 9 tập 1 thường tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc nhất. Các bài tập trong trang 37 và 38 SGK thường xoay quanh việc xác định hàm số, vẽ đồ thị hàm số, và giải các bài toán liên quan đến ứng dụng của hàm số bậc nhất trong thực tế.
Trước khi đi vào giải các bài tập cụ thể, chúng ta cần ôn lại một số kiến thức cơ bản về hàm số bậc nhất:
Các bài tập trong trang 37 thường yêu cầu học sinh xác định hàm số bậc nhất dựa vào các thông tin cho trước. Ví dụ:
Bài 1: Xác định hàm số y = ax + b biết rằng đồ thị của hàm số đi qua hai điểm A(1; 2) và B(-1; 0).
Lời giải: Thay tọa độ của hai điểm A và B vào phương trình y = ax + b, ta có hệ phương trình:
Giải hệ phương trình này, ta được a = 1 và b = 1. Vậy hàm số cần tìm là y = x + 1.
Các bài tập trong trang 38 thường liên quan đến việc vẽ đồ thị hàm số và giải các bài toán ứng dụng. Ví dụ:
Bài 2: Vẽ đồ thị của hàm số y = 2x - 1.
Lời giải:
Để giải các bài tập về hàm số bậc nhất một cách hiệu quả, các em có thể áp dụng một số mẹo sau:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 9 tập 1 hoặc trên các trang web học toán online uy tín như giaitoan.edu.vn.
Hàm số bậc nhất có rất nhiều ứng dụng trong thực tế, ví dụ như:
Hy vọng với những kiến thức và phương pháp giải bài tập được trình bày trong bài viết này, các em sẽ tự tin hơn khi đối mặt với các bài toán về hàm số bậc nhất trong chương trình Toán 9 tập 1. Chúc các em học tập tốt!