Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 109, 110, 111 sách giáo khoa Toán 9 tập 2.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong các kỳ thi sắp tới.
Xét bảng tần số tương đối đã lập ở Ví dụ 1 về tuổi của các thành viên trong lớp hội hoạ (Bảng 10.13b). Hai biểu đồ sau biểu diễn dữ liệu cho trong bảng đó: Sử dụng các biểu đồ đã cho để trả lời hai câu hỏi dưới đây. Đối với mỗi câu hỏi hãy cho biết em đã chọn biểu đồ nào và giải thích sự lựa chọn đó. a) Nhóm học sinh ở độ tuổi nào chiếm số đông nhất trong lớp? Tần số tương đối ứng với nhóm đó gấp bao nhiêu lần tần số tương đối của nhóm có ít học sinh nhất? b) Nhóm nào có số học sinh chiếm
Trả lời câu hỏi Hoạt động 2 trang 109SGK Toán 9 Cùng khám phá
Xét bảng tần số tương đối đã lập ở Ví dụ 1 về tuổi của các thành viên trong lớp hội hoạ (Bảng 10.13b). Hai biểu đồ sau biểu diễn dữ liệu cho trong bảng đó:
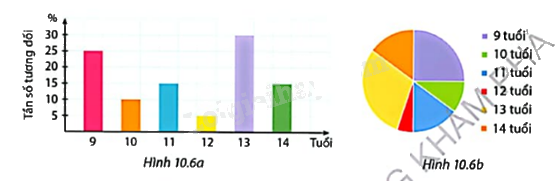
Sử dụng các biểu đồ đã cho để trả lời hai câu hỏi dưới đây. Đối với mỗi câu hỏi hãy cho biết em đã chọn biểu đồ nào và giải thích sự lựa chọn đó.
a) Nhóm học sinh ở độ tuổi nào chiếm số đông nhất trong lớp? Tần số tương đối ứng với nhóm đó gấp bao nhiêu lần tần số tương đối của nhóm có ít học sinh nhất?
b) Nhóm nào có số học sinh chiếm một phần tư sĩ số lớp? Tổng số học sinh những nhóm nào chiếm nửa sĩ số lớp?
Phương pháp giải:
Đọc kĩ dữ liệu đề bài và trả lời câu hỏi.
Lời giải chi tiết:
a) Em chọn biểu đồ Hình 10.6a vì nhìn vào đó dễ dàng xác định tần số tương đối ứng với mỗi nhóm.
Nhóm học sinh ở độ tuổi 13 chiếm số đông nhất trong lớp. Tần số tương đối ứng với nhóm đó gấp 6 lần tần số tương đối của nhóm có ít học sinh nhất ở độ tuổi 12.
b) ) Em chọn biểu đồ Hình 10.6b vì nhìn vào đó dễ dàng xác định nhóm số học sinh chiếm một phần tư sĩ số của cả lớp.
Nhóm độ tuổi 9 có số học sinh chiếm một phần tư sĩ số lớp. Tổng số học sinh những nhóm (9;10;11), (11;12;13), (12;13;14), (9;10;14) chiếm nửa sĩ số lớp.
Trả lời câu hỏi Luyện tập 3 trang 111SGK Toán 9 Cùng khám phá
Ban chấp hành Công đoàn điều tra lương của một số công nhân trong nhà máy và thống kê trong bảng sau:

a) Vẽ biểu đồ tần số tương đối dạng cột và dạng hình quạt tròn biểu diễn bảng thống kê do Công đoàn nhà máy cung cấp.
b) Từ biểu đồ cột, có nhận xét gì về sự chênh lệch tỉ lệ công nhân giữa nhóm lương thấp nhất và nhóm lương cao nhất?
c) Nếu số công nhân này đại diện được cho toàn nhà máy có thể nói số công nhân của nhà máy hưởng mức lương dưới 8 triệu đồng chiếm tỉ lệ bao nhiêu?
d) Ban chấp hành Công đoàn định đề nghị nhà máy trợ cấp cho nhóm công nhân có mức lương dưới 6 triệu đồng. Hỏi có bao nhiêu người đề nghị hưởng trợ cấp, biết rằng nhà máy có 640 công nhân?
Phương pháp giải:
Vẽ biểu đồ tần số dạng cột và dạng hình quạt tròn.
Nhìn vào biểu đồ để trả lời câu hỏi.
Dựa vào công thức tính tần số tương đối: \({f_i} = \frac{{{n_i}}}{N}.100\% \)
Lời giải chi tiết:
a) Biểu đồ tần số dạng cột:
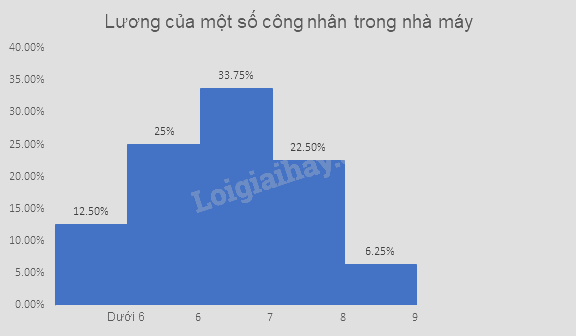
Biểu đồ tần số dạng hình quạt tròn
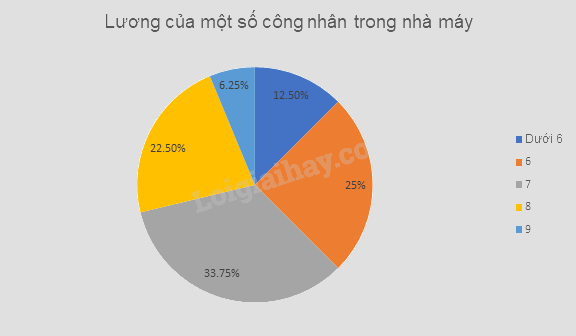
b) Sự chênh lệch tỉ lệ công nhân giữa nhóm lương thấp nhất và nhóm lương cao nhất là 27,5%.
c) Nếu số công nhân này đại diện được cho toàn nhà máy có thể nói số công nhân của nhà máy hưởng mức lương dưới 8 triệu đồng chiếm 71,25%.
d) Số người đề nghị hưởng trợ cấp là: \(\frac{{12,5.640}}{{100}} = 80\) người.
Trả lời câu hỏi Hoạt động 2 trang 109SGK Toán 9 Cùng khám phá
Xét bảng tần số tương đối đã lập ở Ví dụ 1 về tuổi của các thành viên trong lớp hội hoạ (Bảng 10.13b). Hai biểu đồ sau biểu diễn dữ liệu cho trong bảng đó:
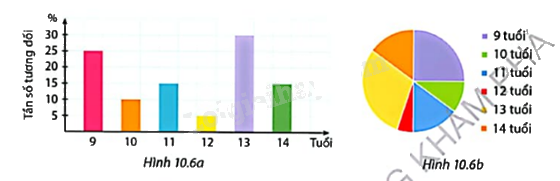
Sử dụng các biểu đồ đã cho để trả lời hai câu hỏi dưới đây. Đối với mỗi câu hỏi hãy cho biết em đã chọn biểu đồ nào và giải thích sự lựa chọn đó.
a) Nhóm học sinh ở độ tuổi nào chiếm số đông nhất trong lớp? Tần số tương đối ứng với nhóm đó gấp bao nhiêu lần tần số tương đối của nhóm có ít học sinh nhất?
b) Nhóm nào có số học sinh chiếm một phần tư sĩ số lớp? Tổng số học sinh những nhóm nào chiếm nửa sĩ số lớp?
Phương pháp giải:
Đọc kĩ dữ liệu đề bài và trả lời câu hỏi.
Lời giải chi tiết:
a) Em chọn biểu đồ Hình 10.6a vì nhìn vào đó dễ dàng xác định tần số tương đối ứng với mỗi nhóm.
Nhóm học sinh ở độ tuổi 13 chiếm số đông nhất trong lớp. Tần số tương đối ứng với nhóm đó gấp 6 lần tần số tương đối của nhóm có ít học sinh nhất ở độ tuổi 12.
b) ) Em chọn biểu đồ Hình 10.6b vì nhìn vào đó dễ dàng xác định nhóm số học sinh chiếm một phần tư sĩ số của cả lớp.
Nhóm độ tuổi 9 có số học sinh chiếm một phần tư sĩ số lớp. Tổng số học sinh những nhóm (9;10;11), (11;12;13), (12;13;14), (9;10;14) chiếm nửa sĩ số lớp.
Trả lời câu hỏi Luyện tập 3 trang 111SGK Toán 9 Cùng khám phá
Ban chấp hành Công đoàn điều tra lương của một số công nhân trong nhà máy và thống kê trong bảng sau:

a) Vẽ biểu đồ tần số tương đối dạng cột và dạng hình quạt tròn biểu diễn bảng thống kê do Công đoàn nhà máy cung cấp.
b) Từ biểu đồ cột, có nhận xét gì về sự chênh lệch tỉ lệ công nhân giữa nhóm lương thấp nhất và nhóm lương cao nhất?
c) Nếu số công nhân này đại diện được cho toàn nhà máy có thể nói số công nhân của nhà máy hưởng mức lương dưới 8 triệu đồng chiếm tỉ lệ bao nhiêu?
d) Ban chấp hành Công đoàn định đề nghị nhà máy trợ cấp cho nhóm công nhân có mức lương dưới 6 triệu đồng. Hỏi có bao nhiêu người đề nghị hưởng trợ cấp, biết rằng nhà máy có 640 công nhân?
Phương pháp giải:
Vẽ biểu đồ tần số dạng cột và dạng hình quạt tròn.
Nhìn vào biểu đồ để trả lời câu hỏi.
Dựa vào công thức tính tần số tương đối: \({f_i} = \frac{{{n_i}}}{N}.100\% \)
Lời giải chi tiết:
a) Biểu đồ tần số dạng cột:
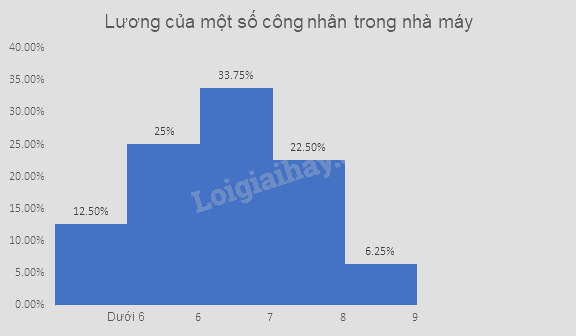
Biểu đồ tần số dạng hình quạt tròn
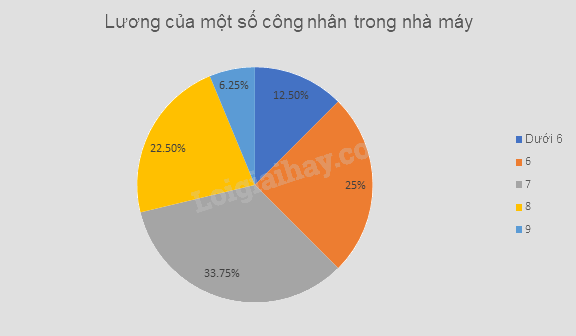
b) Sự chênh lệch tỉ lệ công nhân giữa nhóm lương thấp nhất và nhóm lương cao nhất là 27,5%.
c) Nếu số công nhân này đại diện được cho toàn nhà máy có thể nói số công nhân của nhà máy hưởng mức lương dưới 8 triệu đồng chiếm 71,25%.
d) Số người đề nghị hưởng trợ cấp là: \(\frac{{12,5.640}}{{100}} = 80\) người.
Mục 2 của chương trình Toán 9 tập 2 thường tập trung vào các chủ đề như hàm số bậc nhất, hàm số bậc hai, hệ phương trình bậc hai hai ẩn. Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập trong mục này là vô cùng quan trọng để đạt kết quả tốt trong các bài kiểm tra và kỳ thi cuối năm.
Bài tập này thường yêu cầu học sinh xác định hệ số a, b trong hàm số y = ax + b. Để giải bài tập này, các em cần hiểu rõ định nghĩa của hàm số bậc nhất và cách xác định các hệ số.
Bài tập này thường liên quan đến việc vẽ đồ thị hàm số bậc nhất. Để vẽ đồ thị, các em cần xác định ít nhất hai điểm thuộc đồ thị và nối chúng lại với nhau.
Bài tập này thường yêu cầu học sinh giải các bài toán thực tế liên quan đến hàm số bậc nhất. Để giải bài toán này, các em cần chuyển đổi bài toán thực tế thành bài toán toán học và sử dụng các kiến thức đã học để giải.
Ví dụ: Một người đi xe đạp với vận tốc 15km/h. Hỏi sau 2 giờ người đó đi được bao nhiêu km?
Giải:
Gọi x là thời gian đi (giờ), y là quãng đường đi được (km). Ta có hàm số y = 15x. Khi x = 2, y = 15 * 2 = 30. Vậy sau 2 giờ người đó đi được 30km.
Ngoài các bài tập trong SGK, các em cũng có thể gặp các dạng bài tập sau:
Để học tốt môn Toán 9, các em có thể tham khảo các tài liệu sau:
Hy vọng với những hướng dẫn chi tiết và đầy đủ trên đây, các em sẽ tự tin hơn trong việc giải các bài tập mục 2 trang 109, 110, 111 SGK Toán 9 tập 2. Chúc các em học tốt và đạt kết quả cao trong các kỳ thi sắp tới!