Chào mừng các em học sinh đến với bài giải chi tiết mục 2 trang 124, 125 SGK Toán 9 tập 1 trên giaitoan.edu.vn. Bài viết này sẽ cung cấp cho các em lời giải đầy đủ, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, hỗ trợ các em trong quá trình học tập môn Toán.
Trong Hình 5.63, \(\widehat {AOB} = {70^o}\). a) Sử dụng thước đo góc, xác định số đo các góc nội tiếp AMB, ANB, APB chắn cung AB. b) Nhận xét về mối liên hệ giữa số đo các góc nội tiếp trên với số đo cung nhỏ AB.
Trả lời câu hỏi Vận dụng trang 125SGK Toán 9 Cùng khám phá
Quay lại bài toán ở phần Khởi động (Hình 5.60). Các cung nhỏ AB, BC, CD, DE và AE của lồng đèn ông sao có số đo bằng nhau. Tính số đo mỗi cung, từ đó tính số đo góc CAD của cánh sao.
Phương pháp giải:
Trong một đường tròn, số đo góc của nội tiếp bằng một nửa số đo cung bị chắn bởi góc đó.
Lời giải chi tiết:
Vì cung nhỏ AB, BC, CD, DE và AE của lồng đèn ông sao có số đo bằng nhau nên số đo mỗi cung đó bằng \(\frac{{{{360}^o}}}{5} = {72^o}\).
Vì góc CAD là góc nội tiếp chắn cung nhỏ CD nên \(\widehat {CAD} = \frac{1}{2}{.72^o} = {36^o}\).
Trả lời câu hỏi Luyện tập 2 trang 125 SGK Toán 9 Cùng khám phá
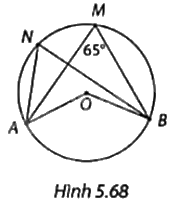
Tính số đo các góc ANB, AOB và cung lớn AB trong Hình 5.68.
Phương pháp giải:
Trong một đường tròn:
+ Số đo góc của nội tiếp bằng một nửa số đo cung bị chắn bởi góc đó.
+ Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
Lời giải chi tiết:
Vì góc AMB và góc ANB là các góc nội tiếp cùng chắn cung nhỏ AB của (O) nên \(\widehat {ANB} = \widehat {AMB} = {65^o}\) và số đo cung nhỏ AB là \({2.65^o} = {130^o}\).
Vì góc AOB là góc ở tâm chắn cung nhỏ AB nên \(\widehat {AOB} = {130^o}\).
Số đo cung lớn AB là: \({360^o} - {130^o} = {230^o}\).
Trả lời câu hỏi Hoạt động 2 trang 124 SGK Toán 9 Cùng khám phá
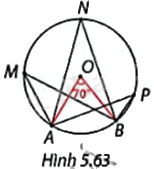
Trong Hình 5.63, \(\widehat {AOB} = {70^o}\).
a) Sử dụng thước đo góc, xác định số đo các góc nội tiếp AMB, ANB, APB chắn cung AB.
b) Nhận xét về mối liên hệ giữa số đo các góc nội tiếp trên với số đo cung nhỏ AB.
Phương pháp giải:
a) Sử dụng thước đo để xác định số đo các góc nội tiếp AMB, ANB, APB.
b) Các góc nội tiếp trên bằng nửa số đo cung nhỏ AB.
Lời giải chi tiết:
a) Ta đo được số đo các góc nội tiếp AMB, ANB, APB đều bằng 35 độ.
b) Ta có: Góc AOB là góc ở tâm chắn cung nhỏ AB nên số đo cung nhỏ AB bằng 70 độ.
Do đó, các góc nội tiếp trên bằng nửa số đo cung nhỏ AB.
Trả lời câu hỏi Luyện tập 2 trang 125 SGK Toán 9 Cùng khám phá
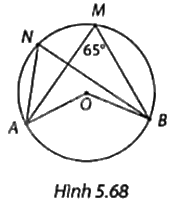
Tính số đo các góc ANB, AOB và cung lớn AB trong Hình 5.68.
Phương pháp giải:
Trong một đường tròn:
+ Số đo góc của nội tiếp bằng một nửa số đo cung bị chắn bởi góc đó.
+ Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
Lời giải chi tiết:
Vì góc AMB và góc ANB là các góc nội tiếp cùng chắn cung nhỏ AB của (O) nên \(\widehat {ANB} = \widehat {AMB} = {65^o}\) và số đo cung nhỏ AB là \({2.65^o} = {130^o}\).
Vì góc AOB là góc ở tâm chắn cung nhỏ AB nên \(\widehat {AOB} = {130^o}\).
Số đo cung lớn AB là: \({360^o} - {130^o} = {230^o}\).
Trả lời câu hỏi Vận dụng trang 125SGK Toán 9 Cùng khám phá
Quay lại bài toán ở phần Khởi động (Hình 5.60). Các cung nhỏ AB, BC, CD, DE và AE của lồng đèn ông sao có số đo bằng nhau. Tính số đo mỗi cung, từ đó tính số đo góc CAD của cánh sao.
Phương pháp giải:
Trong một đường tròn, số đo góc của nội tiếp bằng một nửa số đo cung bị chắn bởi góc đó.
Lời giải chi tiết:
Vì cung nhỏ AB, BC, CD, DE và AE của lồng đèn ông sao có số đo bằng nhau nên số đo mỗi cung đó bằng \(\frac{{{{360}^o}}}{5} = {72^o}\).
Vì góc CAD là góc nội tiếp chắn cung nhỏ CD nên \(\widehat {CAD} = \frac{1}{2}{.72^o} = {36^o}\).
Trả lời câu hỏi Hoạt động 2 trang 124 SGK Toán 9 Cùng khám phá
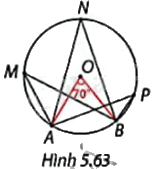
Trong Hình 5.63, \(\widehat {AOB} = {70^o}\).
a) Sử dụng thước đo góc, xác định số đo các góc nội tiếp AMB, ANB, APB chắn cung AB.
b) Nhận xét về mối liên hệ giữa số đo các góc nội tiếp trên với số đo cung nhỏ AB.
Phương pháp giải:
a) Sử dụng thước đo để xác định số đo các góc nội tiếp AMB, ANB, APB.
b) Các góc nội tiếp trên bằng nửa số đo cung nhỏ AB.
Lời giải chi tiết:
a) Ta đo được số đo các góc nội tiếp AMB, ANB, APB đều bằng 35 độ.
b) Ta có: Góc AOB là góc ở tâm chắn cung nhỏ AB nên số đo cung nhỏ AB bằng 70 độ.
Do đó, các góc nội tiếp trên bằng nửa số đo cung nhỏ AB.
Mục 2 của chương trình Toán 9 tập 1 thường tập trung vào các kiến thức về hàm số bậc nhất. Các bài tập trong mục này yêu cầu học sinh vận dụng các kiến thức đã học để xác định hàm số, vẽ đồ thị hàm số, và giải các bài toán liên quan đến hàm số.
Để giúp các em hiểu rõ hơn về nội dung bài tập, chúng ta sẽ đi vào phân tích từng bài tập cụ thể:
Bài tập này yêu cầu học sinh xác định các hệ số a và b của hàm số bậc nhất y = ax + b dựa vào các thông tin đã cho. Ví dụ, đề bài có thể cho biết đồ thị hàm số đi qua hai điểm, hoặc cho biết giá trị của y khi x bằng một giá trị cụ thể.
Để vẽ đồ thị hàm số bậc nhất, học sinh cần xác định ít nhất hai điểm thuộc đồ thị. Sau đó, nối hai điểm này lại với nhau để được đồ thị hàm số.
Các bài toán ứng dụng hàm số bậc nhất thường liên quan đến các tình huống thực tế, ví dụ như tính quãng đường đi được của một vật chuyển động đều, hoặc tính tiền lương của một người lao động.
Để giải các bài tập về hàm số bậc nhất một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:
Ví dụ 1: Cho hàm số y = 2x - 1. Hãy xác định hệ số a và b của hàm số.
Giải: Ta có a = 2 và b = -1.
Ví dụ 2: Vẽ đồ thị hàm số y = x + 2.
Giải:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập tương tự trong SGK Toán 9 tập 1 và các tài liệu tham khảo khác.
Hy vọng rằng bài giải chi tiết mục 2 trang 124, 125 SGK Toán 9 tập 1 trên giaitoan.edu.vn sẽ giúp các em hiểu rõ hơn về hàm số bậc nhất và tự tin giải các bài tập liên quan. Chúc các em học tập tốt!
| Bài tập | Nội dung chính |
|---|---|
| Bài 1 | Xác định hàm số bậc nhất |
| Bài 2 | Vẽ đồ thị hàm số bậc nhất |
| Bài 3 | Giải bài toán ứng dụng |