Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài tập 6.7 trang 6 SGK Toán 9 tập 2 một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong các kỳ thi.
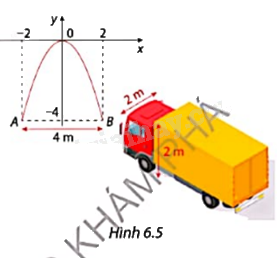
Cổng của một hội chợ được thiết kế theo hình parabol là một phần của đồ thị hàm số y = -x2. Khoảng cách giữa hai chân cổng là 4 m (Hình 6.5). Hỏi một chiếc xe tải có chiều rộng 2 m vào cao 2 m có thể đi qua cổng được không?
Đề bài
Cổng của một hội chợ được thiết kế theo hình parabol là một phần của đồ thị hàm số y = -x2. Khoảng cách giữa hai chân cổng là 4 m (Hình 6.5). Hỏi một chiếc xe tải có chiều rộng 2 m vào cao 2 m có thể đi qua cổng được không?
Phương pháp giải - Xem chi tiết
Thay y = 2 tìm x.
Lời giải chi tiết
Chiều cao của cổng là h = - y = -(4)2 = 16 (m)
Tại điểm xe có chiều cao 2m. Thay y = 2 ta có -2 = - x2
x = \( \pm \sqrt 2 \)
Độ rộng của cổng tại đó là:
\(\sqrt 2 .2 \approx 2,8m\)
Vì 2,8 m > 2 m nên chiếc xe có thể đi qua được.
Bài tập 6.7 trang 6 SGK Toán 9 tập 2 thuộc chương Hàm số bậc nhất. Để giải bài tập này, học sinh cần nắm vững kiến thức về hàm số bậc nhất, cách xác định hệ số góc và tung độ gốc, cũng như các tính chất của hàm số.
Bài tập 6.7 thường yêu cầu học sinh xác định hàm số bậc nhất dựa vào các thông tin cho trước, chẳng hạn như đồ thị, hai điểm thuộc đồ thị, hoặc hệ số góc và tung độ gốc. Để giải bài tập này, ta cần:
Đề bài: Xác định hàm số bậc nhất y = ax + b biết đồ thị của hàm số đi qua hai điểm A(1; 2) và B(-1; 0).
Lời giải:
Ngoài dạng bài tập xác định hàm số bậc nhất dựa vào hai điểm, còn có các dạng bài tập khác như:
Để giải các dạng bài tập này, học sinh cần nắm vững lý thuyết, áp dụng các công thức và phương pháp giải phù hợp.
Để củng cố kiến thức, bạn có thể tự giải các bài tập sau:
Bài tập 6.7 trang 6 SGK Toán 9 tập 2 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và các ứng dụng của nó. Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trong bài viết này, bạn sẽ tự tin hơn trong việc giải các bài tập tương tự.
Chúc bạn học tập tốt!