Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 2 tại giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 35, 36, 37 của sách giáo khoa Toán 9 tập 2.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong các kỳ thi. Hãy cùng khám phá và chinh phục những bài toán này nhé!
Với các điểm trong Hình 7.12, bạn An cho rằng có thể vẽ một đường tròn đi qua cả bốn điểm A, B, C, D còn bạn Bình thì cho rằng có thể vẽ được một đường tròn đi qua cả bốn điểm A, B, C, E. Hãy vẽ đường tròn đi qua ba điểm A, B, C và cho biết bạn nào đúng.
Trả lời câu hỏi Hoạt động 2 trang 36SGK Toán 9 Cùng khám phá
Giải thích vì sao giao điểm của hai đường chéo của hình chữ nhật và hình vuông cách đều bốn đỉnh của chúng.
Phương pháp giải:
Trong hình chữ nhật, hình vuông ta có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.
Lời giải chi tiết:
Theo tính chất của hình chữ nhật và hình vuông: Trong hình chữ nhật, hình vuông ta có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường nên giao điểm của hai đường chéo của hình chữ nhật và hình vuông cách đều bốn đỉnh của chúng.
Trả lời câu hỏi Luyện tập 1 trang 36SGK Toán 9 Cùng khám phá
Vẽ một tứ giác nội tiếp hình tròn và một tứ giác không nội tiếp đường tròn.
Phương pháp giải:
Dựa vào một tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp.
Lời giải chi tiết:
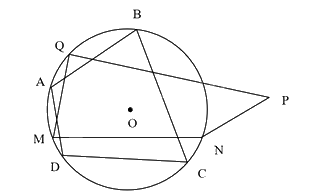
Trên hình vẽ tứ giác ABCD là tứ giác nội tiếp đường tròn, tứ giác MNPQ là tứ giác không nội tiếp đường tròn.
Trả lời câu hỏi Hoạt động 1 trang 35 SGK Toán 9 Cùng khám phá
Với các điểm trong Hình 7.12, bạn An cho rằng có thể vẽ một đường tròn đi qua cả bốn điểm A, B, C, D còn bạn Bình thì cho rằng có thể vẽ được một đường tròn đi qua cả bốn điểm A, B, C, E. Hãy vẽ đường tròn đi qua ba điểm A, B, C và cho biết bạn nào đúng.
Phương pháp giải:
Dùng compa vẽ đường tròn đi qua 3 điểm A, B,C và kết luận.
Lời giải chi tiết:
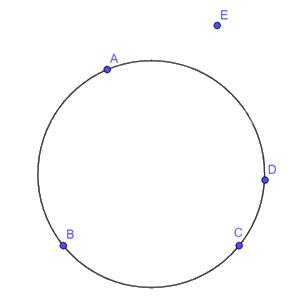
Theo hình vẽ bạn An đúng.
Trả lời câu hỏi Luyện tập 2 trang 37SGK Toán 9 Cùng khám phá
Xác định tâm và đường kính của đường tròn ngoại tiếp hình vuông có cạnh 3 cm.
Phương pháp giải:
Đường tròn ngoại tiếp hình vuông có tâm là giao điểm của hai đường chéo và bán kính là nửa đường chéo.
Lời giải chi tiết:
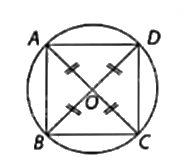
Gọi O là giao điểm của hai đường chéo AC và BD. Khi đó, đường tròn ngoại tiếp hình vuông ABCD có tâm là O và bán kính bằng \(\frac{1}{2}\)AC.
Vì tam giác ABC vuông tại B nên
AC = \(\sqrt {A{B^2} + B{C^2}} = \sqrt {{3^2} + {3^2}} = 3\sqrt 2 \) cm
Do đó R = \(\frac{1}{2}\)AC = \(\frac{1}{2}\). \(3\sqrt 2 \) = \(\frac{{3\sqrt 2 }}{2}\)cm
Trả lời câu hỏi Hoạt động 1 trang 35 SGK Toán 9 Cùng khám phá
Với các điểm trong Hình 7.12, bạn An cho rằng có thể vẽ một đường tròn đi qua cả bốn điểm A, B, C, D còn bạn Bình thì cho rằng có thể vẽ được một đường tròn đi qua cả bốn điểm A, B, C, E. Hãy vẽ đường tròn đi qua ba điểm A, B, C và cho biết bạn nào đúng.
Phương pháp giải:
Dùng compa vẽ đường tròn đi qua 3 điểm A, B,C và kết luận.
Lời giải chi tiết:
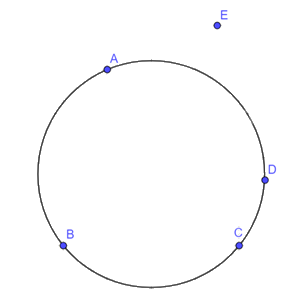
Theo hình vẽ bạn An đúng.
Trả lời câu hỏi Luyện tập 1 trang 36SGK Toán 9 Cùng khám phá
Vẽ một tứ giác nội tiếp hình tròn và một tứ giác không nội tiếp đường tròn.
Phương pháp giải:
Dựa vào một tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp.
Lời giải chi tiết:
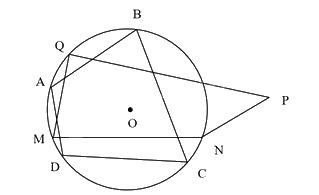
Trên hình vẽ tứ giác ABCD là tứ giác nội tiếp đường tròn, tứ giác MNPQ là tứ giác không nội tiếp đường tròn.
Trả lời câu hỏi Hoạt động 2 trang 36SGK Toán 9 Cùng khám phá
Giải thích vì sao giao điểm của hai đường chéo của hình chữ nhật và hình vuông cách đều bốn đỉnh của chúng.
Phương pháp giải:
Trong hình chữ nhật, hình vuông ta có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.
Lời giải chi tiết:
Theo tính chất của hình chữ nhật và hình vuông: Trong hình chữ nhật, hình vuông ta có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường nên giao điểm của hai đường chéo của hình chữ nhật và hình vuông cách đều bốn đỉnh của chúng.
Trả lời câu hỏi Luyện tập 2 trang 37SGK Toán 9 Cùng khám phá
Xác định tâm và đường kính của đường tròn ngoại tiếp hình vuông có cạnh 3 cm.
Phương pháp giải:
Đường tròn ngoại tiếp hình vuông có tâm là giao điểm của hai đường chéo và bán kính là nửa đường chéo.
Lời giải chi tiết:
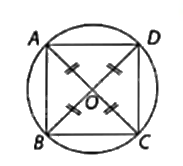
Gọi O là giao điểm của hai đường chéo AC và BD. Khi đó, đường tròn ngoại tiếp hình vuông ABCD có tâm là O và bán kính bằng \(\frac{1}{2}\)AC.
Vì tam giác ABC vuông tại B nên
AC = \(\sqrt {A{B^2} + B{C^2}} = \sqrt {{3^2} + {3^2}} = 3\sqrt 2 \) cm
Do đó R = \(\frac{1}{2}\)AC = \(\frac{1}{2}\). \(3\sqrt 2 \) = \(\frac{{3\sqrt 2 }}{2}\)cm
Mục 1 của SGK Toán 9 tập 2 thường tập trung vào một chủ đề quan trọng trong chương trình học. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững lý thuyết cơ bản, các định nghĩa, tính chất và công thức liên quan. Việc hiểu rõ bản chất của vấn đề sẽ giúp các em tiếp cận bài toán một cách logic và tìm ra lời giải chính xác.
Trong mục 1 trang 35, 36, 37, các em có thể gặp các dạng bài tập sau:
Dưới đây là hướng dẫn giải chi tiết từng bài tập trong mục 1 trang 35, 36, 37 SGK Toán 9 tập 2:
Đề bài: (Giả sử đề bài là một bài toán cụ thể về hàm số bậc nhất). Lời giải: (Giải thích chi tiết từng bước giải, kèm theo các bước biến đổi và kết luận). Ví dụ: Để xác định hàm số bậc nhất có dạng y = ax + b, ta cần tìm giá trị của a và b. Sử dụng các điểm cho trước, ta có thể lập hệ phương trình và giải để tìm ra a và b. Sau đó, thay các giá trị này vào phương trình để có hàm số bậc nhất cần tìm.
Đề bài: (Giả sử đề bài là một bài toán về hệ phương trình). Lời giải: (Giải thích chi tiết từng bước giải, kèm theo các bước biến đổi và kết luận). Ví dụ: Để giải hệ phương trình, ta có thể sử dụng phương pháp thế hoặc phương pháp cộng đại số. Chọn phương pháp phù hợp và thực hiện các phép biến đổi để tìm ra giá trị của x và y.
Đề bài: (Giả sử đề bài là một bài toán về bất phương trình). Lời giải: (Giải thích chi tiết từng bước giải, kèm theo các bước biến đổi và kết luận). Ví dụ: Để giải bất phương trình, ta cần thực hiện các phép biến đổi tương đương để đưa bất phương trình về dạng đơn giản hơn. Sau đó, tìm ra tập nghiệm của bất phương trình.
Để giải các bài tập Toán 9 một cách nhanh chóng và hiệu quả, các em có thể áp dụng một số mẹo sau:
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, các em nên luyện tập thêm các bài tập tương tự trong sách bài tập hoặc trên các trang web học toán online. Việc luyện tập thường xuyên sẽ giúp các em tự tin hơn trong các kỳ thi.
| Công thức | Mô tả |
|---|---|
| y = ax + b | Hàm số bậc nhất |
| Δ = b2 - 4ac | Biệt thức của phương trình bậc hai |
Hy vọng với những hướng dẫn chi tiết và hữu ích này, các em sẽ giải quyết thành công các bài tập trong mục 1 trang 35, 36, 37 SGK Toán 9 tập 2. Chúc các em học tập tốt!