Chào mừng các em học sinh đến với bài giải bài tập 4.25 trang 90 SGK Toán 9 tập 1 trên giaitoan.edu.vn. Bài tập này thuộc chương Hàm số bậc nhất và ứng dụng. Chúng tôi sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.
Giaitoan.edu.vn là nền tảng học toán online uy tín, cung cấp đầy đủ các bài giải SGK Toán 9, bài tập trắc nghiệm, và các tài liệu học tập hữu ích khác.
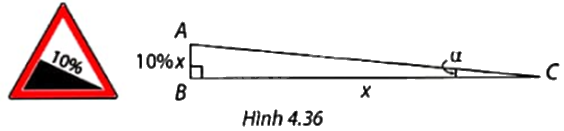
Trong các biển báo dốc nguy hiểm, độ nghiêng của dốc thường được ghi ở dạng phần trăm. Chẳng hạn độ nghiêng 10% nghĩa là dốc có chiều cao AB bằng 10% độ dài BC (Hình 4.36). Dốc 10% có góc nghiêng \(\alpha \) so với phương nằm ngang (làm tròn đến đơn vị độ) là A. \({12^o}\). B. \({10^o}\). C. \({8^o}\). D. \({6^o}\).
Đề bài
Trong các biển báo dốc nguy hiểm, độ nghiêng của dốc thường được ghi ở dạng phần trăm. Chẳng hạn độ nghiêng 10% nghĩa là dốc có chiều cao AB bằng 10% độ dài BC (Hình 4.36). Dốc 10% có góc nghiêng \(\alpha \) so với phương nằm ngang (làm tròn đến đơn vị độ) là
A. \({12^o}\).
B. \({10^o}\).
C. \({8^o}\).
D. \({6^o}\).
Phương pháp giải - Xem chi tiết
Tam giác ABC vuông tại B nên \(\tan C = \frac{{AB}}{{BC}}\), do đó tính được góc \(\alpha \).
Lời giải chi tiết
Tam giác ABC vuông tại B nên
\(\tan C = \frac{{AB}}{{BC}} = \frac{{10\% BC}}{{BC}} = 0,1\), do đó, \(\alpha \approx {6^o}\)
Chọn D
Bài tập 4.25 trang 90 SGK Toán 9 tập 1 yêu cầu chúng ta giải một bài toán liên quan đến hàm số bậc nhất. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về hàm số bậc nhất, bao gồm định nghĩa, dạng tổng quát, và các tính chất của hàm số.
Hàm số bậc nhất có dạng y = ax + b (với a ≠ 0). Trong đó:
Để giải các bài toán liên quan đến hàm số bậc nhất, chúng ta thường sử dụng các phương pháp sau:
Trước khi đi vào giải chi tiết, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Bài toán 4.25 thường yêu cầu chúng ta:
(Ở đây sẽ là lời giải chi tiết cho bài tập 4.25, bao gồm các bước giải, giải thích rõ ràng và kết luận. Ví dụ, nếu bài toán yêu cầu tìm hàm số y = ax + b đi qua hai điểm A(x1, y1) và B(x2, y2), lời giải sẽ bao gồm các bước sau:)
Để giúp các em hiểu rõ hơn về cách giải bài tập 4.25, chúng ta sẽ xem xét một ví dụ minh họa:
Ví dụ: Tìm hàm số y = ax + b đi qua hai điểm A(1, 2) và B(2, 4).
Lời giải:
Thay tọa độ của điểm A và B vào phương trình y = ax + b, ta được hệ phương trình:
2 = a + b
4 = 2a + b
Giải hệ phương trình, ta được a = 2 và b = 0. Vậy hàm số cần tìm là y = 2x.
Ngoài bài tập 4.25, các em có thể tham khảo thêm các bài tập tương tự sau:
Để giải bài tập về hàm số bậc nhất một cách hiệu quả, các em cần lưu ý những điều sau:
Bài tập 4.25 trang 90 SGK Toán 9 tập 1 là một bài tập quan trọng giúp các em củng cố kiến thức về hàm số bậc nhất. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em sẽ giải bài tập này một cách dễ dàng và hiệu quả. Chúc các em học tốt!