Chào mừng các em học sinh đến với bài giải bài tập 4.7 trang 86 SGK Toán 9 tập 1 trên giaitoan.edu.vn. Bài tập này thuộc chương Hàm số bậc nhất và là một phần quan trọng trong việc củng cố kiến thức về hàm số.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và tự tin làm bài tập.
Giải tam giác ABC vuông tại A, biết: a) \(AC = 11cm,\widehat C = {60^o}\); b) \(BC = 20cm,\widehat C = {35^o}\); c) \(AB = 7cm,AC = 12cm\); d) \(AB = 9cm,BC = 20cm\).
Đề bài
Giải tam giác ABC vuông tại A, biết:
a) \(AC = 11cm,\widehat C = {60^o}\);
b) \(BC = 20cm,\widehat C = {35^o}\);
c) \(AB = 7cm,AC = 12cm\);
d) \(AB = 9cm,BC = 20cm\).
Phương pháp giải - Xem chi tiết
Tam giác ABC vuông tại A nên:
a) \(\widehat B = {90^o} - \widehat C\), \(AB = AC.\tan C\), \(BC = \frac{{AC}}{{\cos C}}\)
b) \(\widehat B = {90^o} - \widehat C\), \(AB = BC.\sin C\), \(AC = BC.\cos C\)
c) \(B{C^2} = A{B^2} + A{C^2}\), \(\tan B = \frac{{AC}}{{AB}} = \frac{{12}}{7}\) từ đó tính được góc B, \(\widehat C = {90^o} - \widehat B\).
d) \(A{C^2} = B{C^2} - A{B^2}\), \(\sin C = \frac{{AB}}{{BC}}\) từ đó tính được góc C, \(\widehat B = {90^o} - \widehat C\).
Lời giải chi tiết
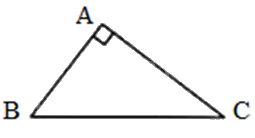
Tam giác ABC vuông tại A nên:
a) \(\widehat B = {90^o} - \widehat C = {90^o} - {60^o} = {30^o}\).
\(AB = AC.\tan C = 11.\tan {60^o} = 11\sqrt 3 \approx 19,1cm\),
\(BC = \frac{{AC}}{{\cos C}} = \frac{{11}}{{\cos {{60}^o}}} = 22\left( {cm} \right)\)
b) \(\widehat B = {90^o} - \widehat C = {90^o} - {35^o} = {55^o}\).
\(AB = BC.\sin C = 20.\sin {35^o} \approx 11,5cm\),
\(AC = BC.\cos C = 20.\cos {35^o} \approx 16,4\left( {cm} \right)\).
c) \(B{C^2} = A{B^2} + A{C^2} = {7^2} + {12^2} = 193\) nên \(BC \approx 13,9cm\).
\(\tan B = \frac{{AC}}{{AB}} = \frac{{12}}{7}\) nên \(\widehat B \approx {59^o}45'\), \(\widehat C = {90^o} - \widehat B \approx {30^o}15'\).
d) \(A{C^2} = B{C^2} - A{B^2} = {20^2} - {9^2} = 319\) nên \(AC \approx 17,9cm\).
\(\sin C = \frac{{AB}}{{BC}} = \frac{9}{{20}}\) nên \(\widehat C \approx {26^o}45'\), \(\widehat B = {90^o} - \widehat C \approx {63^o}15'\).
Bài tập 4.7 trang 86 SGK Toán 9 tập 1 yêu cầu chúng ta xét hàm số y = (m-2)x + 3. Để hàm số này là hàm số bậc nhất, điều kiện cần và đủ là hệ số của x khác 0, tức là m-2 ≠ 0. Bài viết này sẽ đi sâu vào phân tích điều kiện này và cung cấp lời giải chi tiết, giúp học sinh hiểu rõ bản chất của bài toán.
Hàm số y = ax + b được gọi là hàm số bậc nhất khi và chỉ khi a ≠ 0. Trong trường hợp bài tập 4.7, a = m-2. Do đó, để y = (m-2)x + 3 là hàm số bậc nhất, chúng ta cần đảm bảo m-2 ≠ 0.
Để tìm giá trị của m, chúng ta giải phương trình m-2 ≠ 0. Điều này tương đương với m ≠ 2.
Kết luận: Hàm số y = (m-2)x + 3 là hàm số bậc nhất khi và chỉ khi m ≠ 2.
Khi m = 2, hàm số trở thành y = 0x + 3, hay y = 3. Đây là một hàm số hằng, không phải là hàm số bậc nhất. Hàm số hằng là một trường hợp đặc biệt, trong đó giá trị của y không phụ thuộc vào giá trị của x.
Ví dụ 1: Nếu m = 3, hàm số trở thành y = (3-2)x + 3 = x + 3. Đây là hàm số bậc nhất vì hệ số của x là 1, khác 0.
Ví dụ 2: Nếu m = 1, hàm số trở thành y = (1-2)x + 3 = -x + 3. Đây cũng là hàm số bậc nhất vì hệ số của x là -1, khác 0.
Ví dụ 3: Nếu m = 2, hàm số trở thành y = (2-2)x + 3 = 3. Đây là hàm số hằng, không phải hàm số bậc nhất.
Việc nắm vững định nghĩa hàm số bậc nhất là nền tảng quan trọng để học các kiến thức nâng cao hơn về hàm số, như đồ thị hàm số, hệ số góc, và ứng dụng của hàm số trong thực tế. Hiểu rõ điều kiện a ≠ 0 giúp chúng ta phân biệt được hàm số bậc nhất với các loại hàm số khác, từ đó áp dụng đúng phương pháp giải toán.
Ngoài bài tập 4.7, còn rất nhiều dạng bài tập liên quan đến hàm số bậc nhất mà các em có thể luyện tập, như:
Bài tập 4.7 trang 86 SGK Toán 9 tập 1 là một bài tập cơ bản nhưng quan trọng trong chương Hàm số bậc nhất. Việc hiểu rõ định nghĩa hàm số bậc nhất và điều kiện m ≠ 2 là chìa khóa để giải quyết bài toán này một cách chính xác và hiệu quả. Hy vọng bài viết này đã cung cấp cho các em những kiến thức hữu ích và giúp các em tự tin hơn trong việc học toán.
Hãy tiếp tục luyện tập và khám phá thêm nhiều bài tập thú vị khác trên giaitoan.edu.vn!