Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9 tập 2. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài toán phức tạp.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập. Bài viết này sẽ tập trung vào việc giải các câu hỏi trang 59 và 60 SGK Toán 9 tập 2, cung cấp các bước giải chi tiết và giải thích rõ ràng.
Hãy cho biết các tam giác đều vẽ thêm được trong Bước 2 và Bước 3 có bằng nhau không. Giải thích.
Trả lời câu hỏi Yêu cầu Hoạt động 1 trang 59 SGK Toán 9 Cùng khám phá
Hãy cho biết các tam giác đều vẽ thêm được trong Bước 2 và Bước 3 có bằng nhau không. Giải thích.
Phương pháp giải:
Xem Hoạt động 1 để nhận xét.
Lời giải chi tiết:
Các tam giác đều vẽ thêm được trong Bước 2 và Bước 3 có bằng nhau vì ta đã cài mặc định chiều quay và góc quay giống nhau 60o.
Trả lời câu hỏi Yêu cầu Hoạt động 2 trang 60 SGK Toán 9 Cùng khám phá
Hãy kiểm tra xem các tam giác vẽ trong hoạ tiết có phải tam giác đều hay không?
Phương pháp giải:
Xem Hoạt động 2 để nhận xét.
Lời giải chi tiết:
Các tam giác vẽ trong hoạ tiết phải là các tam giác đều.
Trả lời câu hỏi Thực hành trang 60SGK Toán 9 Cùng khám phá
Dùng phần mềm GeoGebra để vẽ các hoạ tiết trang trí sau:
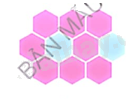
Phương pháp giải:
Xem Hoạt động 1 và Hoạt động 2 để vẽ tương tự.
Lời giải chi tiết:
Hình 1.
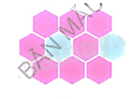
Bước 1. Vẽ một hình lục giác.
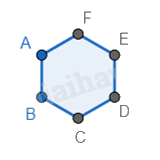
Bước 2. Vẽ liên tiếp các hình lục giác xung quanh bằng cách chọn cạnh của hình lục giác đã vẽ.
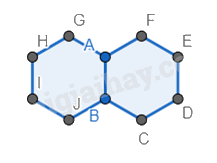
Tương tự cho đến khi vẽ đủ 10 hình như ảnh mẫu.
Bước 3. Đổi màu lại hình lục giác.
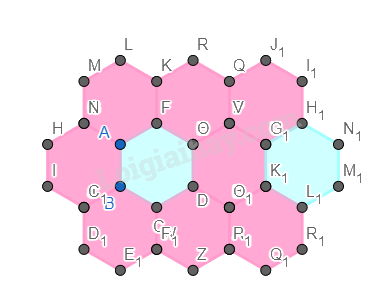
Bước 4. Chỉnh độ dày của các cạnh về 0.
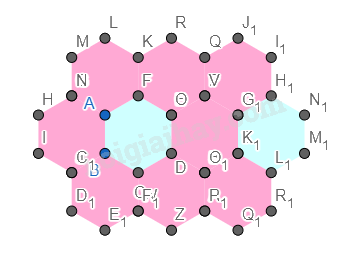
Ẩn cách đỉnh của hình lục giác.
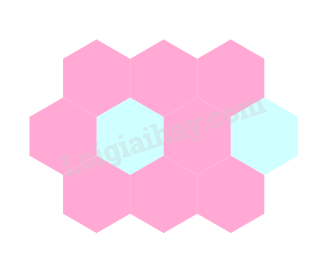
Ta được hình cần vẽ.
Hình 2.
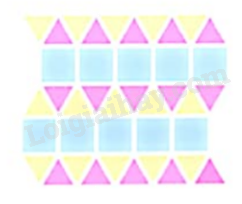
Bước 1. Vẽ 5 hình vuông nối nhau thành một hàng ngang.
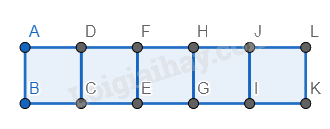
Bước 2. Vẽ các hình tam giác đều có cạnh là cạnh phía trên và dưới của các hình vuông vừa vẽ.
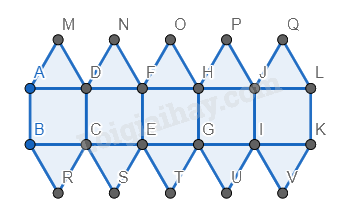
Bước 3. Vẽ các hình tam giác đều các cạnh là cạnh bên trái của các hình tam giác vừa vẽ.
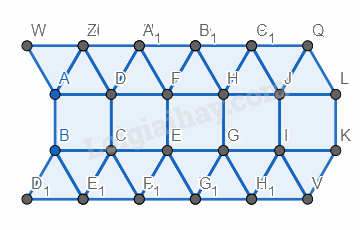
Bước 4. Vẽ các hình vuông có các cạnh là cạnh bên dưới của cách hình tam giác vừa vẽ.
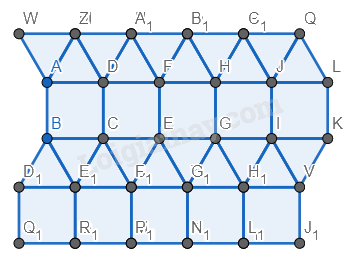
Bước 5. Vẽ thêm các tam giác phía dưới hình vuông vừa vẽ giống bước 2 và bước 3.
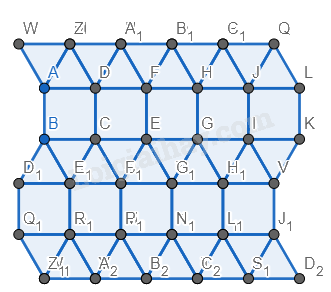
Bước 6. Đổi màu lại hình.
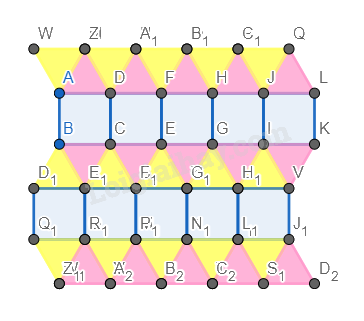
Bước 7. Chỉnh độ dày của các cạnh về 0.
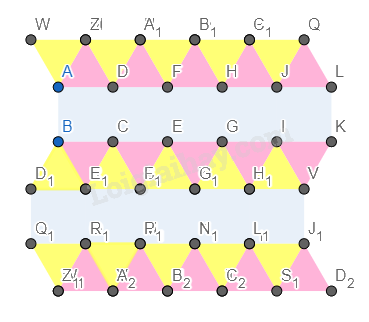
Ẩn cách đỉnh của hình.

Ta được hình cần vẽ.
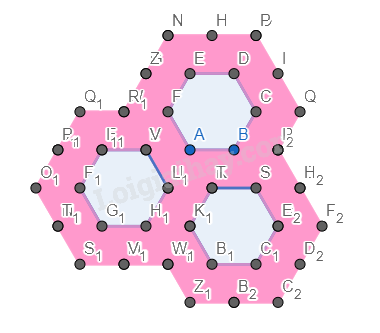
Hình 3.

Bước 1. Vẽ một hình lục giác đều.
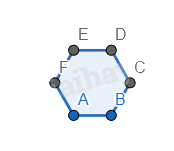
Bước 2. Vẽ các hình tam giác đều có cạnh là cạnh xung quanh của hình lục giác đều.
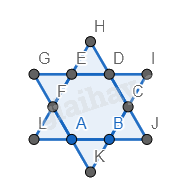
Bước 3. Vẽ thêm các tam giác đều mới có cạnh là cạnh của tam giác đều.
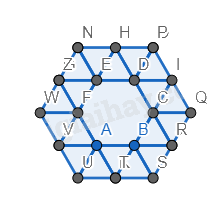
Bước 4. Vẽ thêm hai hình lục giác đều mới có cạnh là cạnh của tam giác đều.
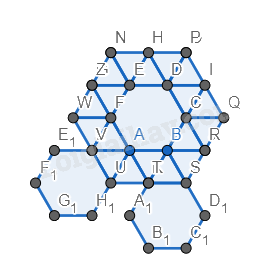
Bước 5. Vẽ thêm các tam giác đều xung quanh như bước 2 và bước 3.
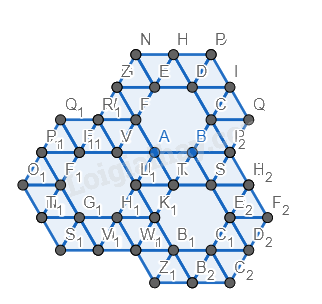
Bước 6. Đổi màu lại hình.
Bước 7. Chỉnh độ dày của các cạnh về 0.
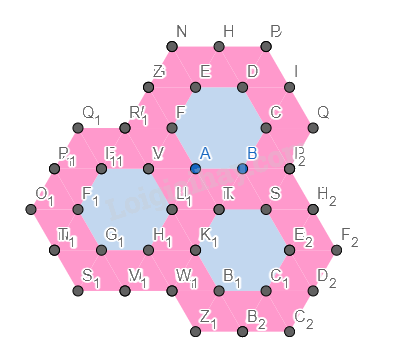
Ẩn cách đỉnh của hình.

Ta được hình cần vẽ.
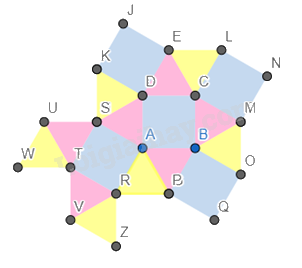
Hình 4.
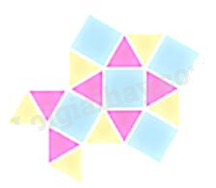
Bước 1. Vẽ một hình vuông.
Bước 2. Vẽ các hình tam giác đều có cạnh là các cạnh của hình vuông.
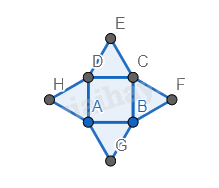
Bước 3. Vẽ các hình vuông và hình tam giác đều có cạnh là các cạnh của hình tam giác đều và so le với nhau.
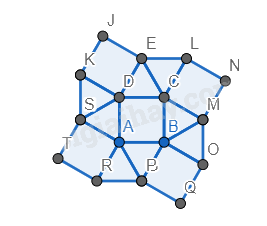
Bước 4. Vẽ thêm các tam giác đều vào xung quanh hình vuông phía dưới bên trái có cạnh là cạnh hình vuông
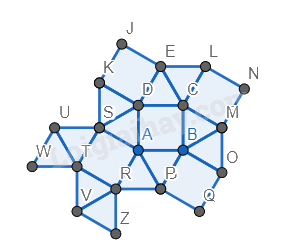
Bước 5. Đổi màu lại hình.
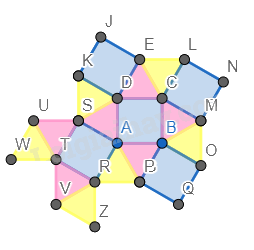
Bước 6. Chỉnh độ dày của các cạnh về 0.
Ẩn cách đỉnh của hình.

Ta được hình cần vẽ.
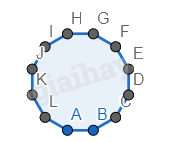
Hình 5.

Bước 1. Vẽ một hình bát giác đều.
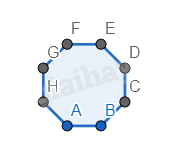
Bước 2. Vẽ 4 hình vuông ở 4 góc của hình bát giác, cạnh bằng với cạnh của hình bát giác.
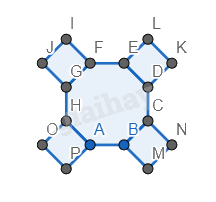
Bước 3. Tương tự, vẽ các hình bát giác bên trái, bên dưới hình bát giác.
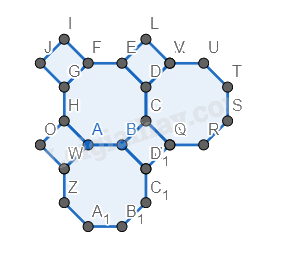
Bước 4. Vẽ tương tự bước 2, 3 để có 6 hình bát giác đều và các hình vuông xung quanh.
Bước 5. Đổi màu lại hình.
Bước 6. Chỉnh độ dày của các cạnh về 0.
Ẩn cách đỉnh của hình.

Ta được hình cần vẽ.
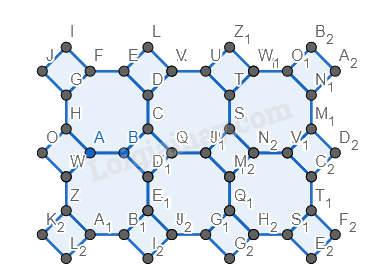
Hình 6.

Bước 1. Vẽ một đa diện đều có 12 cạnh.
Bước 2. Vẽ các hình vuông xung quanh đa diện đều có cạnh bằng cạnh của đa diện và nằm so le với nhau.
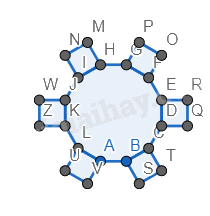
Bước 3. Vẽ các hình lục giác đều xung quanh đa diện đều có cạnh bằng cạnh của đa diện và nằm so le với nhau (giữa các hình vuông).
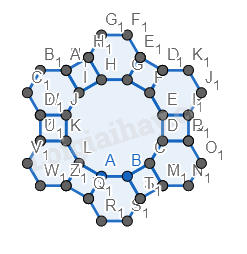
Bước 4. Vẽ hai hình đa giác đều 12 cạnh có cạnh bằng cạnh của hình vuông, nằm phía dưới hình vừa vẽ.
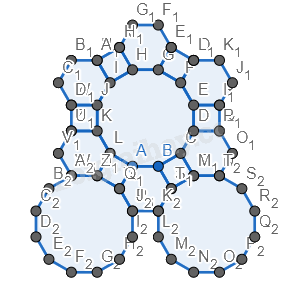
Bước 5. Vẽ thêm các hình vuông và lục giác đều xung quanh hai hình đa giác vừa vẽ.
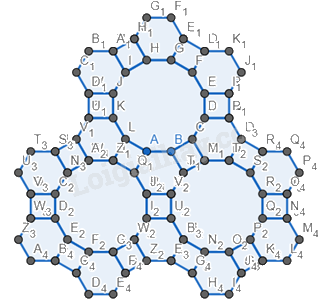
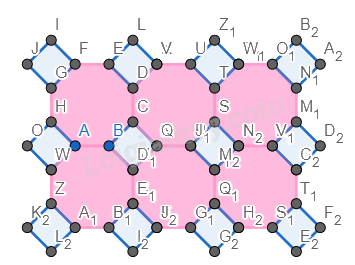
Bước 6. Đổi màu lại hình.
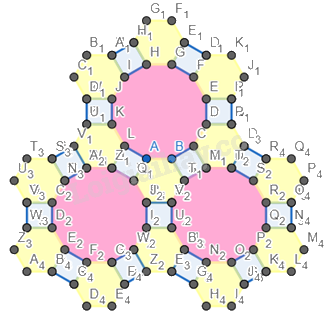
Bước 7. Chỉnh độ dày của các cạnh về 0.
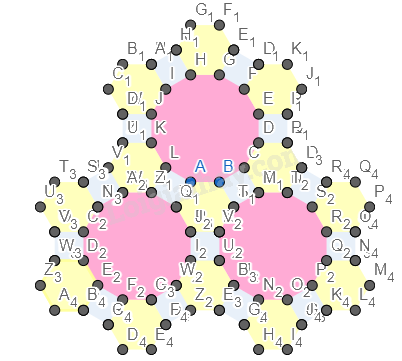
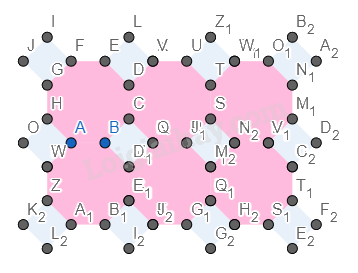
Ẩn cách đỉnh của hình.
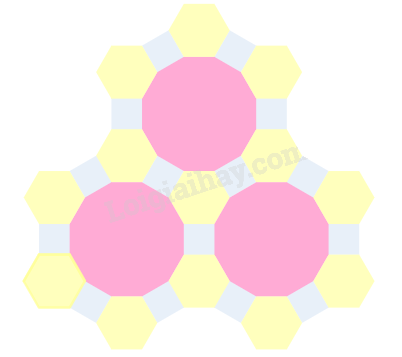
Ta được hình cần vẽ.
Trả lời câu hỏi Yêu cầu Hoạt động 1 trang 59 SGK Toán 9 Cùng khám phá
Hãy cho biết các tam giác đều vẽ thêm được trong Bước 2 và Bước 3 có bằng nhau không. Giải thích.
Phương pháp giải:
Xem Hoạt động 1 để nhận xét.
Lời giải chi tiết:
Các tam giác đều vẽ thêm được trong Bước 2 và Bước 3 có bằng nhau vì ta đã cài mặc định chiều quay và góc quay giống nhau 60o.
Trả lời câu hỏi Yêu cầu Hoạt động 2 trang 60 SGK Toán 9 Cùng khám phá
Hãy kiểm tra xem các tam giác vẽ trong hoạ tiết có phải tam giác đều hay không?
Phương pháp giải:
Xem Hoạt động 2 để nhận xét.
Lời giải chi tiết:
Các tam giác vẽ trong hoạ tiết phải là các tam giác đều.
Trả lời câu hỏi Thực hành trang 60SGK Toán 9 Cùng khám phá
Dùng phần mềm GeoGebra để vẽ các hoạ tiết trang trí sau:
Phương pháp giải:
Xem Hoạt động 1 và Hoạt động 2 để vẽ tương tự.
Lời giải chi tiết:
Hình 1.
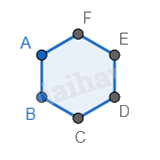
Bước 1. Vẽ một hình lục giác.
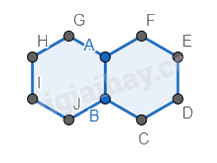
Bước 2. Vẽ liên tiếp các hình lục giác xung quanh bằng cách chọn cạnh của hình lục giác đã vẽ.
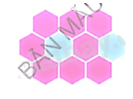
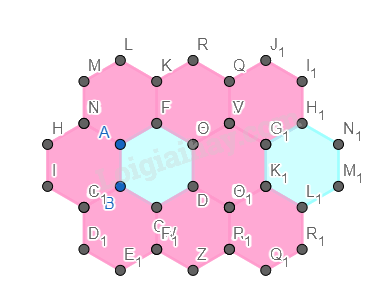
Tương tự cho đến khi vẽ đủ 10 hình như ảnh mẫu.
Bước 3. Đổi màu lại hình lục giác.
Bước 4. Chỉnh độ dày của các cạnh về 0.
Ẩn cách đỉnh của hình lục giác.
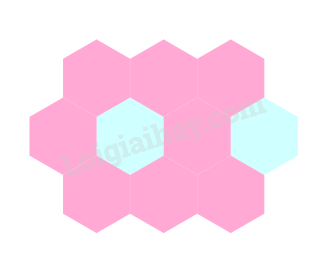
Ta được hình cần vẽ.
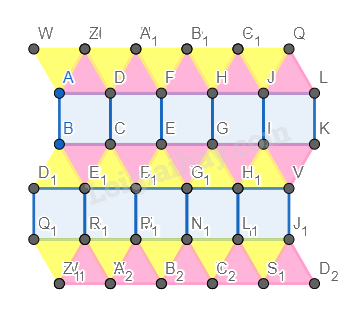
Hình 2.
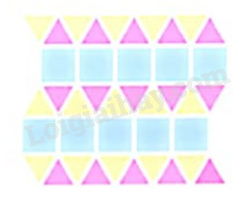
Bước 1. Vẽ 5 hình vuông nối nhau thành một hàng ngang.
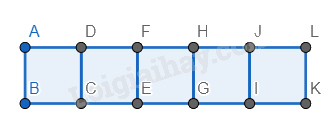
Bước 2. Vẽ các hình tam giác đều có cạnh là cạnh phía trên và dưới của các hình vuông vừa vẽ.
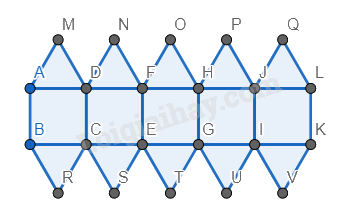
Bước 3. Vẽ các hình tam giác đều các cạnh là cạnh bên trái của các hình tam giác vừa vẽ.
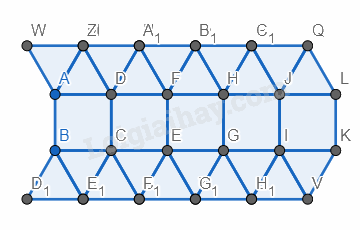
Bước 4. Vẽ các hình vuông có các cạnh là cạnh bên dưới của cách hình tam giác vừa vẽ.
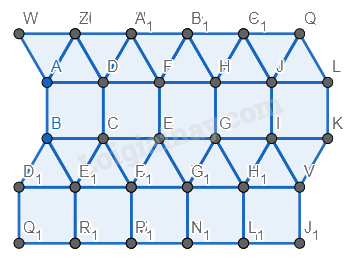
Bước 5. Vẽ thêm các tam giác phía dưới hình vuông vừa vẽ giống bước 2 và bước 3.
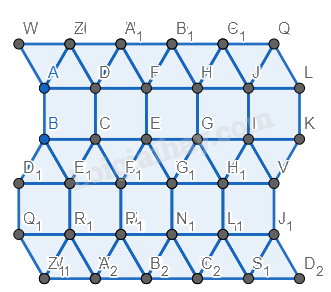
Bước 6. Đổi màu lại hình.
Bước 7. Chỉnh độ dày của các cạnh về 0.
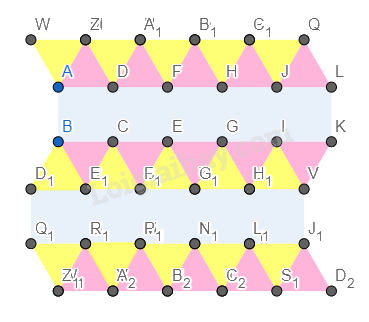
Ẩn cách đỉnh của hình.

Ta được hình cần vẽ.
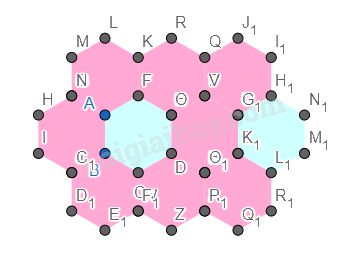
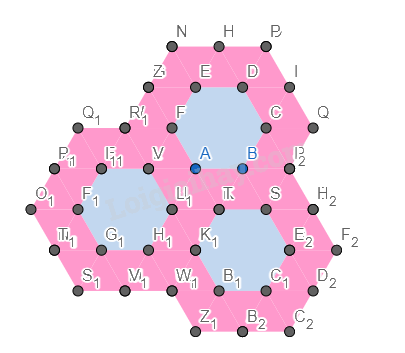
Hình 3.

Bước 1. Vẽ một hình lục giác đều.
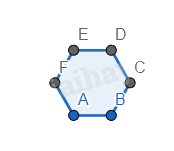
Bước 2. Vẽ các hình tam giác đều có cạnh là cạnh xung quanh của hình lục giác đều.
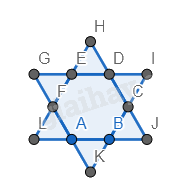
Bước 3. Vẽ thêm các tam giác đều mới có cạnh là cạnh của tam giác đều.
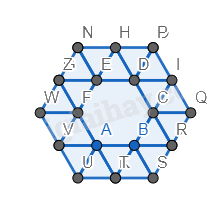
Bước 4. Vẽ thêm hai hình lục giác đều mới có cạnh là cạnh của tam giác đều.
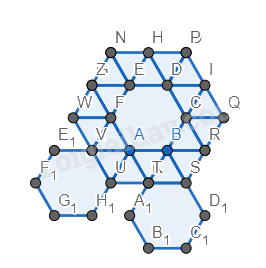
Bước 5. Vẽ thêm các tam giác đều xung quanh như bước 2 và bước 3.
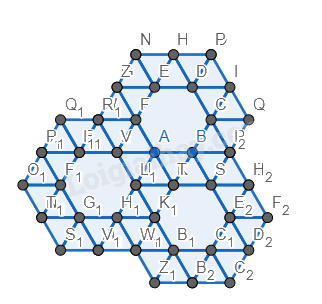
Bước 6. Đổi màu lại hình.
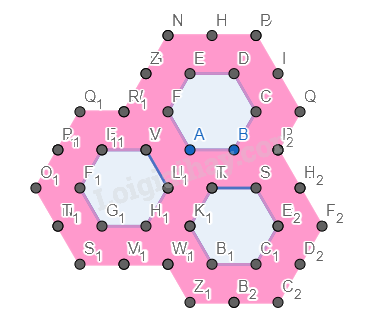
Bước 7. Chỉnh độ dày của các cạnh về 0.
Ẩn cách đỉnh của hình.

Ta được hình cần vẽ.
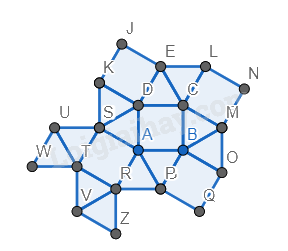
Hình 4.
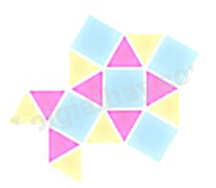
Bước 1. Vẽ một hình vuông.
Bước 2. Vẽ các hình tam giác đều có cạnh là các cạnh của hình vuông.

Bước 3. Vẽ các hình vuông và hình tam giác đều có cạnh là các cạnh của hình tam giác đều và so le với nhau.
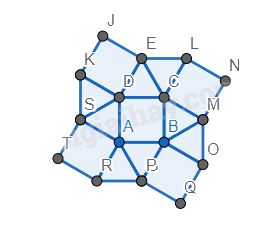
Bước 4. Vẽ thêm các tam giác đều vào xung quanh hình vuông phía dưới bên trái có cạnh là cạnh hình vuông
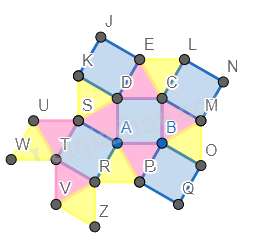
Bước 5. Đổi màu lại hình.
Bước 6. Chỉnh độ dày của các cạnh về 0.
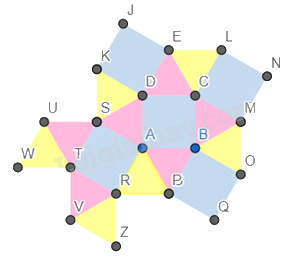
Ẩn cách đỉnh của hình.

Ta được hình cần vẽ.
Hình 5.

Bước 1. Vẽ một hình bát giác đều.
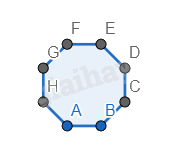
Bước 2. Vẽ 4 hình vuông ở 4 góc của hình bát giác, cạnh bằng với cạnh của hình bát giác.
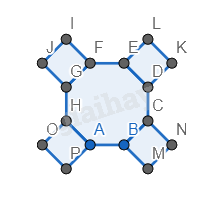
Bước 3. Tương tự, vẽ các hình bát giác bên trái, bên dưới hình bát giác.
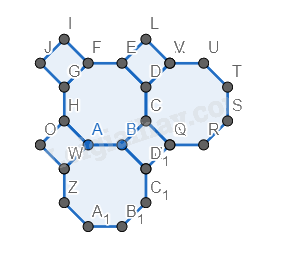
Bước 4. Vẽ tương tự bước 2, 3 để có 6 hình bát giác đều và các hình vuông xung quanh.
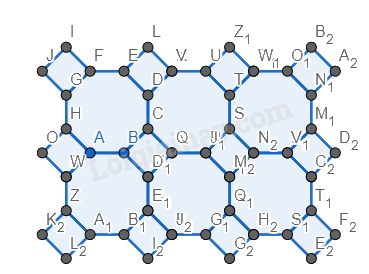
Bước 5. Đổi màu lại hình.
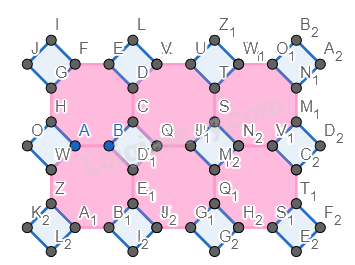
Bước 6. Chỉnh độ dày của các cạnh về 0.
Ẩn cách đỉnh của hình.

Ta được hình cần vẽ.
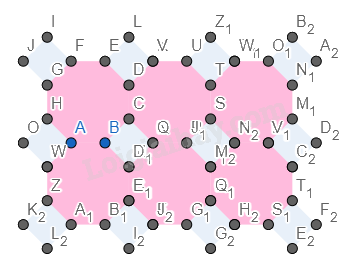
Hình 6.

Bước 1. Vẽ một đa diện đều có 12 cạnh.
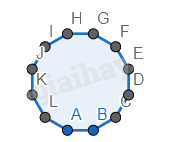
Bước 2. Vẽ các hình vuông xung quanh đa diện đều có cạnh bằng cạnh của đa diện và nằm so le với nhau.
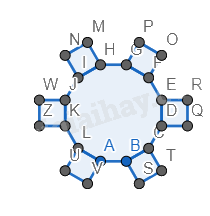
Bước 3. Vẽ các hình lục giác đều xung quanh đa diện đều có cạnh bằng cạnh của đa diện và nằm so le với nhau (giữa các hình vuông).
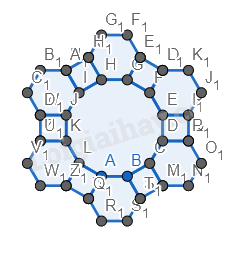
Bước 4. Vẽ hai hình đa giác đều 12 cạnh có cạnh bằng cạnh của hình vuông, nằm phía dưới hình vừa vẽ.
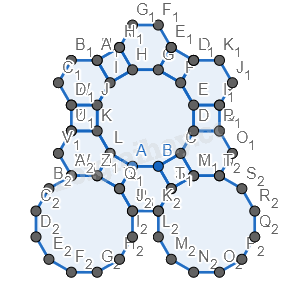
Bước 5. Vẽ thêm các hình vuông và lục giác đều xung quanh hai hình đa giác vừa vẽ.
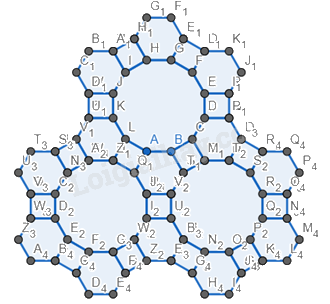
Bước 6. Đổi màu lại hình.
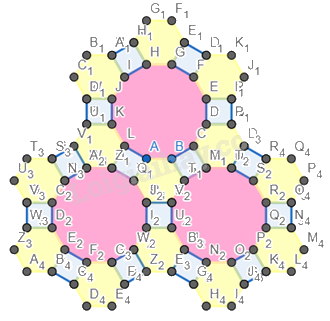
Bước 7. Chỉnh độ dày của các cạnh về 0.
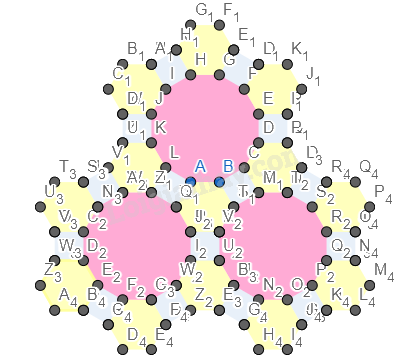
Ẩn cách đỉnh của hình.
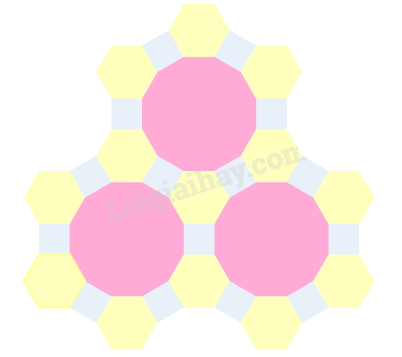
Ta được hình cần vẽ.
Trang 59 và 60 của SGK Toán 9 tập 2 thường chứa các bài tập liên quan đến hàm số bậc hai, đồ thị hàm số và ứng dụng của hàm số bậc hai trong giải quyết các bài toán thực tế. Để giải quyết hiệu quả các bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
Bài 1: (Giả sử bài tập yêu cầu tìm tọa độ đỉnh của parabol y = x2 - 4x + 3)
Lời giải:
Bài 2: (Giả sử bài tập yêu cầu vẽ đồ thị hàm số y = 2x2 + x - 1)
Lời giải:
Bài 3: (Giả sử bài tập yêu cầu tìm giá trị của x để hàm số y = -x2 + 6x - 5 đạt giá trị lớn nhất)
Lời giải:
Vì a = -1 < 0 nên hàm số đạt giá trị lớn nhất tại đỉnh của parabol. Áp dụng công thức tính tọa độ đỉnh như đã trình bày ở trên, ta tìm được xI = 3. Vậy hàm số đạt giá trị lớn nhất khi x = 3.
Bài 4: (Giả sử bài tập yêu cầu xác định phương trình parabol đi qua ba điểm A(0; 1), B(1; 2), C(-1; 0))
Lời giải:
Giả sử phương trình parabol có dạng y = ax2 + bx + c. Thay tọa độ các điểm A, B, C vào phương trình, ta được hệ phương trình:
| a | b | c | |
|---|---|---|---|
| A(0; 1) | 0 | 0 | 1 |
| B(1; 2) | 1 | 1 | 2 |
| C(-1; 0) | 1 | -1 | 0 |
Giải hệ phương trình này, ta tìm được a, b, c và xác định được phương trình parabol.
Hy vọng với những hướng dẫn chi tiết và dễ hiểu trên, bạn sẽ tự tin giải quyết các bài tập trang 59 và 60 SGK Toán 9 tập 2. Chúc bạn học tập tốt!