Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Trong bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho mục 2 trang 37 và 38 sách giáo khoa Toán 9 tập 2.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong các kỳ thi sắp tới.
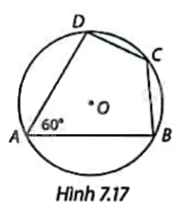
Trong Hình 7.17, tứ giác ABCD nội tiếp đường tròn (O). Hãy tính số đo cung nhỏ BD, cung lớn BD, từ đó suy ra số đo góc C. Em có nhận xét gì về tổng hai góc A và C.
Trả lời câu hỏi Luyện tập 3 trang 38 SGK Toán 9 Cùng khám phá
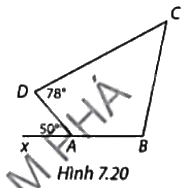
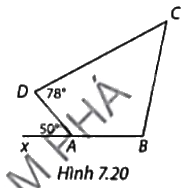
Tính số đo các góc B và C của tứ giác ABCD trong Hình 7.20. Biết tứ giác ABCD nội tiếp được trong đường tròn.
Phương pháp giải:
Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng \({180^o}\).
Lời giải chi tiết:
Ta có tứ giác ABCD nội tiếp đường tròn nên \(\widehat D + \widehat B = {180^o}\) suy ra \(\widehat B = {180^o} - \widehat D = {180^o} - {78^o} = {102^o}\)
Ta có \(\widehat {xAB} = {180^o}\)(góc bẹt) suy ra
\(\widehat {DAB} = {180^o} - \widehat {xAD} = {180^o} - {50^o} = {130^o}\)
Mà \(\widehat C + \widehat {DAB} = {180^o}\) suy ra
\(\widehat C = {180^o} - \widehat {DAB} = {180^o} - {130^o} = {50^o}\).
Trả lời câu hỏi Hoạt động 3 trang 37SGK Toán 9 Cùng khám phá
Trong Hình 7.17, tứ giác ABCD nội tiếp đường tròn (O). Hãy tính số đo cung nhỏ BD, cung lớn BD, từ đó suy ra số đo góc C. Em có nhận xét gì về tổng hai góc A và C.
Phương pháp giải:
Dùng tính chất góc nội tiếp bằng nửa cung bị chắn để tính cung BD nhỏ và cung BD lớn, sau đó suy ra góc C và kết luận.
Lời giải chi tiết:
Ta có \(\widehat A\) chắn cung nhỏ BD nên \(\widehat{A}=\frac{1}{2}sđ\overset\frown{BD}\) nhỏ suy ra \(sđ\overset\frown{BD}\) nhỏ \( = 2.\widehat A = {2.60^o} = {120^o}\)
Suy ra \(sđ\overset\frown{BD}\) lớn = \({360^o} - {120^o} = {240^o}\)
Mà \(\widehat C\) chắn cung lớn BD nên \(\widehat{C}=\frac{1}{2}sđ\overset\frown{BD}\) lớn = \(\frac{1}{2}{.240^o} = {120^o}\)
Ta có tổng hai góc \(\widehat A + \widehat C = {60^o} + {120^o} = {180^o}\).
Trả lời câu hỏi Vận dụng trang 38 SGK Toán 9 Cùng khám phá
Quay lại phần Khởi động, em hãy sử dụng kiến thức được học về tứ giác nội tiếp để giải thích vì sao không thể tìm được vị trí đặt lửa trại phù hợp.
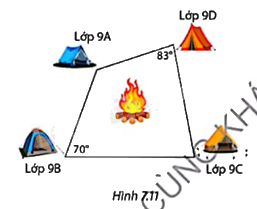
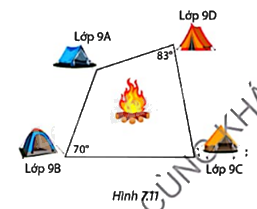
Phần Khởi động: Bốn lớp 9A, 9B, 9C và 9D cùng đi cắm trại. Sử dụng giác kế, các bạn có thể đo được góc tạo bởi các vị trí cắm trại của bốn lớp và vẽ được sơ đồ cắm trại như Hình 7.11. Hỏi có thể tìm được một vị trí cách đều cả bốn trại để đặt lửa trại không?
Phương pháp giải:
Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng \({180^o}\).
Lời giải chi tiết:
Không thể tìm được vị trí đặt lửa trại phù hợp vì tổng hai góc đối tạo bởi của lớp 9B và 9B là \({83^o} + {70^o} = {153^o} \ne {180^o}\) nên tứ giác 4 vị trí cắm trại không nội tiếp.
Trả lời câu hỏi Hoạt động 3 trang 37SGK Toán 9 Cùng khám phá
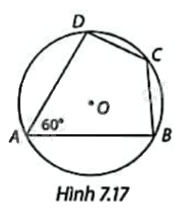
Trong Hình 7.17, tứ giác ABCD nội tiếp đường tròn (O). Hãy tính số đo cung nhỏ BD, cung lớn BD, từ đó suy ra số đo góc C. Em có nhận xét gì về tổng hai góc A và C.
Phương pháp giải:
Dùng tính chất góc nội tiếp bằng nửa cung bị chắn để tính cung BD nhỏ và cung BD lớn, sau đó suy ra góc C và kết luận.
Lời giải chi tiết:
Ta có \(\widehat A\) chắn cung nhỏ BD nên \(\widehat{A}=\frac{1}{2}sđ\overset\frown{BD}\) nhỏ suy ra \(sđ\overset\frown{BD}\) nhỏ \( = 2.\widehat A = {2.60^o} = {120^o}\)
Suy ra \(sđ\overset\frown{BD}\) lớn = \({360^o} - {120^o} = {240^o}\)
Mà \(\widehat C\) chắn cung lớn BD nên \(\widehat{C}=\frac{1}{2}sđ\overset\frown{BD}\) lớn = \(\frac{1}{2}{.240^o} = {120^o}\)
Ta có tổng hai góc \(\widehat A + \widehat C = {60^o} + {120^o} = {180^o}\).
Trả lời câu hỏi Luyện tập 3 trang 38 SGK Toán 9 Cùng khám phá
Tính số đo các góc B và C của tứ giác ABCD trong Hình 7.20. Biết tứ giác ABCD nội tiếp được trong đường tròn.
Phương pháp giải:
Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng \({180^o}\).
Lời giải chi tiết:
Ta có tứ giác ABCD nội tiếp đường tròn nên \(\widehat D + \widehat B = {180^o}\) suy ra \(\widehat B = {180^o} - \widehat D = {180^o} - {78^o} = {102^o}\)
Ta có \(\widehat {xAB} = {180^o}\)(góc bẹt) suy ra
\(\widehat {DAB} = {180^o} - \widehat {xAD} = {180^o} - {50^o} = {130^o}\)
Mà \(\widehat C + \widehat {DAB} = {180^o}\) suy ra
\(\widehat C = {180^o} - \widehat {DAB} = {180^o} - {130^o} = {50^o}\).
Trả lời câu hỏi Vận dụng trang 38 SGK Toán 9 Cùng khám phá
Quay lại phần Khởi động, em hãy sử dụng kiến thức được học về tứ giác nội tiếp để giải thích vì sao không thể tìm được vị trí đặt lửa trại phù hợp.
Phần Khởi động: Bốn lớp 9A, 9B, 9C và 9D cùng đi cắm trại. Sử dụng giác kế, các bạn có thể đo được góc tạo bởi các vị trí cắm trại của bốn lớp và vẽ được sơ đồ cắm trại như Hình 7.11. Hỏi có thể tìm được một vị trí cách đều cả bốn trại để đặt lửa trại không?
Phương pháp giải:
Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng \({180^o}\).
Lời giải chi tiết:
Không thể tìm được vị trí đặt lửa trại phù hợp vì tổng hai góc đối tạo bởi của lớp 9B và 9B là \({83^o} + {70^o} = {153^o} \ne {180^o}\) nên tứ giác 4 vị trí cắm trại không nội tiếp.
Mục 2 của SGK Toán 9 tập 2 tập trung vào việc nghiên cứu hàm số bậc nhất. Đây là một trong những kiến thức nền tảng quan trọng của chương trình Toán học lớp 9, đóng vai trò thiết yếu trong việc xây dựng các kiến thức nâng cao hơn ở các lớp trên. Để hiểu rõ về hàm số bậc nhất, chúng ta cần nắm vững các khái niệm cơ bản như:
Trong mục 2 trang 37 và 38, SGK Toán 9 tập 2 thường xuất hiện các dạng bài tập sau:
Bài 1: Cho hàm số y = 2x - 3. Hãy xác định hệ số a và b của hàm số.
Giải: Hàm số y = 2x - 3 là hàm số bậc nhất với a = 2 và b = -3.
Bài 2: Vẽ đồ thị của hàm số y = -x + 1.
Giải:
Để giải bài tập về hàm số bậc nhất một cách hiệu quả, các em cần lưu ý những điều sau:
Hy vọng với những hướng dẫn chi tiết trên, các em học sinh đã có thể tự tin giải các bài tập trong mục 2 trang 37, 38 SGK Toán 9 tập 2. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!