Chào mừng các em học sinh đến với bài giải bài tập 9.13 trang 83 SGK Toán 9 tập 2 tại giaitoan.edu.vn. Bài tập này thuộc chương hàm số bậc nhất và ứng dụng, một trong những chủ đề quan trọng của chương trình Toán 9.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.
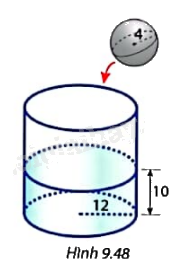
Một chiếc cốc hình trụ có phần đáy bên trong là một hình tròn bán kính bằng 12 cm. Chiều cao của mực nước trong cốc là 10 cm (Hình 9.48). a) Tính thể tích nước trong cốc. b) Thả một quả cầu bằng kim loại có bán kính 4 cm vào cốc cho đến khi quả cầu chìm hẳn xuống đáy cốc và mực nước đứng yên. Hỏi mực nước trong cốc tăng thêm bao nhiêu centimet?
Đề bài
Một chiếc cốc hình trụ có phần đáy bên trong là một hình tròn bán kính bằng 12 cm. Chiều cao của mực nước trong cốc là 10 cm (Hình 9.48).
a) Tính thể tích nước trong cốc.
b) Thả một quả cầu bằng kim loại có bán kính 4 cm vào cốc cho đến khi quả cầu chìm hẳn xuống đáy cốc và mực nước đứng yên. Hỏi mực nước trong cốc tăng thêm bao nhiêu centimet?
Phương pháp giải - Xem chi tiết
Thể tích của hình trụ: \(V = \pi {R^2}h\) (với R là bán kính đáy hình trụ, h là chiều cao)
Thể tích của hình cầu là: \(V = \frac{4}{3}\pi {R^3}\)(với R là bán kính hình cầu)
Lời giải chi tiết
a) Thể tích nước trong cốc hình trụ là:
\(V = \pi {R^2}h = \pi {.12^2}.10 = 1440\pi\)cm3
b) Thể tích quả cầu kim loại là:
\(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {.4^3} = \frac{256}{3}\pi\) cm3
Thể tích nước sau khi thả quả cầu là:
\( 1440\pi + \frac{256}{3}\pi = \frac{4576}{3}\pi\) cm3
Chiều cao mực nước khi đó là:
\(\frac{4576}{3} \pi: (\pi.12^2) \approx 10,6\) cm
Mực nước trong cốc tăng lên là:
10,6 – 10 = 0,6 cm.
Vậy mực nước trong cốc tăng lên khoảng 0,6 cm.
Bài tập 9.13 trang 83 SGK Toán 9 tập 2 yêu cầu học sinh vận dụng kiến thức về phương pháp tiếp tuyến để giải quyết một bài toán thực tế. Bài toán thường liên quan đến việc tìm phương trình tiếp tuyến của một đường cong tại một điểm cho trước, hoặc xác định điều kiện để một đường thẳng là tiếp tuyến của một đường cong.
Đề bài cụ thể của bài tập 9.13 thường có dạng như sau: Cho hàm số y = f(x). Tìm phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = a.
Ví dụ: Cho hàm số y = x2 - 2x + 3. Tìm phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = 1.
Để giải bài tập 9.13 trang 83 SGK Toán 9 tập 2 một cách hiệu quả, các em cần:
Bài tập 9.13 trang 83 SGK Toán 9 tập 2 là một bài tập quan trọng giúp các em củng cố kiến thức về phương pháp tiếp tuyến và ứng dụng của nó. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa trên, các em sẽ tự tin giải quyết bài tập này và các bài tập tương tự một cách hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!