Chào mừng các em học sinh đến với bài giải bài tập 5.39 trang 128 SGK Toán 9 tập 1 trên giaitoan.edu.vn. Bài tập này thuộc chương hàm số bậc nhất và ứng dụng, một trong những chủ đề quan trọng của chương trình Toán 9.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và áp dụng vào các bài tập tương tự.
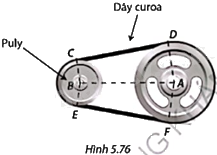
Trong Hình 5.76, hai puly có dạng hình tròn tâm A bán kính 12,5cm và tâm B bán kính 7cm được nối bằng dây curoa. Khoảng cách giữa tâm của hai puly là (AB = 30cm). Đoạn dây CD, EF tiếp xúc với cả hai puly. Tính: a) Độ dài CD và số đo các góc của tứ giác ABCD; b) Độ dài dây curoa. Làm tròn độ dài đến hàng phần mười centimét, số đo góc đến phút.
Đề bài
Trong Hình 5.76, hai puly có dạng hình tròn tâm A bán kính 12,5cm và tâm B bán kính 7cm được nối bằng dây curoa. Khoảng cách giữa tâm của hai puly là \(AB = 30cm\). Đoạn dây CD, EF tiếp xúc với cả hai puly. Tính:
a) Độ dài CD và số đo các góc của tứ giác ABCD;
b) Độ dài dây curoa.
Làm tròn độ dài đến hàng phần mười centimét, số đo góc đến phút.
Phương pháp giải - Xem chi tiết
a) + Kẻ BG vuông góc với AD tại G.
+ Chứng minh tứ giác BCDG là hình chữ nhật suy ra \(CD = BG\), \(BC = DG\)
+ Áp dụng định lí Pythagore vào tam giác ABG vuông tại G để tính BG, AG; tính cos GAB, từ đó tính góc GAB.
+ Tứ giác ABCD có: \(\widehat C + \widehat D + \widehat {DAB} + \widehat {ABC} = {360^o}\), từ đó tính được góc ABC.
b) + Tính số đo cung lớn FD, số đo cung nhỏ CE.
+ Tính độ dài cung lớn FD, độ dài cung nhỏ CE.
+ Độ dài dây curoa là: \({l_{DF}} + {l_{CE}} + CD + EF\).
Lời giải chi tiết
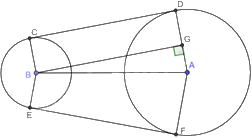
Kẻ BG vuông góc với AD tại G. Suy ra: \(\widehat {BGD} = \widehat {BGA} = {90^o}\).
Vì CD là tiếp tuyến của hai đường tròn (B) và (A) nên \(BC \bot CD,CD \bot AD\) nên \(\widehat {BCD} = \widehat {CDG} = {90^o}\).
Tứ giác BGDC có: \(\widehat {BCD} = \widehat {CDG} = \widehat {BGD} = {90^o}\) nên tứ giác BGDC là hình chữ nhật.
Do đó, \(CD = BG\), \(BC = DG = 7cm\).
Tam giác BGA vuông tại G nên:
+ \(\cos GAB = \frac{{GA}}{{AB}} = \frac{{DA - GD}}{{AB}} = \frac{{5,5}}{{30}} = \frac{{11}}{{60}}\) nên \(\widehat {GAB} \approx {79^o}26'\)
+ \(B{G^2} + G{A^2} = A{B^2}\),
\(BG = \sqrt {A{B^2} - {{\left( {AD - DG} \right)}^2}} = \sqrt {{{30}^2} - {{\left( {12,5 - 7} \right)}^2}} = \frac{{7\sqrt {71} }}{2}\left( {cm} \right)\)
nên \(CD = \frac{{7\sqrt {71} }}{2}cm\)
Chứng minh tương tự ta có: \(EF = \frac{{7\sqrt {71} }}{2}cm\)
Tứ giác ABCD có: \(\widehat C + \widehat D + \widehat {DAB} + \widehat {ABC} = {360^o}\)
\(\widehat {ABC} = {360^o} - \left( {\widehat C + \widehat D + \widehat {DAB}} \right) \approx {360^o} - \left( {{{90}^o} + {{90}^o} + {{79}^o}26'} \right) \approx {100^o}34'\)
b) Chứng minh tương tự phần a ta có:
\(\widehat {FAB} \approx {79^o}26'\), \(\widehat {EBF} \approx {100^o}34'\)
Do đó, \(\widehat {DAF} = \widehat {DAB} + \widehat {FAB} \approx {158^o}52'\).
Do đó, số đo cung nhỏ DF là: \({158^o}52'\).
Suy ra, số đo cung lớn DF là:
\({360^o} - {158^o}52' = {201^o}8'\)
Số đo cung CE nhỏ là: \({158^o}52'\).
Độ dài cung lớn DF là:
\({l_{DF}} = \frac{{\pi {{.12.201}^o}8'}}{{{{180}^o}}} = \frac{{3017\pi }}{{225}}\left( {cm} \right)\)
Độ dài cung nhỏ CE là:
\({l_{CE}} = \frac{{\pi .7,{{5.158}^o}52'}}{{180}} = \frac{{2383\pi }}{{360}}\left( {cm} \right)\)
Độ dài dây curoa là:
\({l_{DF}} + {l_{CE}} + CD + EF \approx \frac{{3017\pi }}{{225}} + \frac{{2383\pi }}{{360}} + 2.\frac{{7\sqrt {71} }}{2} \approx 121,9\left( {cm} \right)\)
Bài tập 5.39 trang 128 SGK Toán 9 tập 1 yêu cầu tìm phương trình đường thẳng là tiếp tuyến của đồ thị hàm số y = -2x + 3 tại điểm có hoành độ x = 1.
Để giải bài tập này, chúng ta cần nắm vững kiến thức về hàm số bậc nhất, đồ thị hàm số và phương pháp tìm phương trình đường thẳng.
Bước 1: Xác định tọa độ điểm tiếp xúc
Khi x = 1, ta có y = -2(1) + 3 = 1. Vậy điểm tiếp xúc là A(1; 1).
Bước 2: Xác định hệ số góc của tiếp tuyến
Hệ số góc của tiếp tuyến chính là hệ số góc của hàm số y = -2x + 3, tức là m = -2.
Bước 3: Viết phương trình đường thẳng tiếp tuyến
Phương trình đường thẳng tiếp tuyến có dạng y = mx + c. Thay m = -2 và tọa độ điểm A(1; 1) vào, ta có:
1 = -2(1) + c
=> c = 3
Vậy phương trình đường thẳng tiếp tuyến là y = -2x + 3.
Để củng cố kiến thức, các em có thể thử giải các bài tập tương tự sau:
Ngoài phương pháp tìm phương trình tiếp tuyến như trên, còn có một số phương pháp khác như sử dụng đạo hàm (dành cho học sinh nâng cao). Việc nắm vững các phương pháp khác nhau sẽ giúp các em giải quyết các bài toán phức tạp hơn một cách hiệu quả.
Ví dụ về ứng dụng của tiếp tuyến trong thực tế:
Trong vật lý, tiếp tuyến có thể được sử dụng để xác định vận tốc tức thời của một vật chuyển động. Trong kinh tế, tiếp tuyến có thể được sử dụng để xác định chi phí biên của một sản phẩm.
Hy vọng bài giải chi tiết này sẽ giúp các em hiểu rõ hơn về cách giải bài tập 5.39 trang 128 SGK Toán 9 tập 1. Chúc các em học tập tốt!
Các em nên tự mình giải bài tập trước khi xem lời giải để rèn luyện kỹ năng và tư duy toán học. Nếu gặp khó khăn, hãy tham khảo lời giải và cố gắng hiểu rõ từng bước giải.
| Khái niệm | Giải thích |
|---|---|
| Hàm số bậc nhất | y = ax + b (a ≠ 0) |
| Tiếp tuyến | Đường thẳng tiếp xúc với đồ thị hàm số tại một điểm |