Chào mừng các em học sinh đến với bài giải chi tiết mục 3 trang 68, 69 SGK Toán 9 tập 1 tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải đầy đủ, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Bài học này tập trung vào việc... (nội dung giới thiệu ngắn gọn về chủ đề bài học)
Tìm công thức tính thể tích V của hình lập phương có cạnh bằng a. Từ đó giải thích vì sao \(a = \sqrt[3]{V}\).
Trả lời câu hỏi Hoạt động 2 trang 68 SGK Toán 9 Cùng khám phá
Tìm công thức tính thể tích V của hình lập phương có cạnh bằng a. Từ đó giải thích vì sao \(a = \sqrt[3]{V}\).
Phương pháp giải:
Sử dụng công thức tính thể tích V của hình lập phương.
Lời giải chi tiết:
Công thức tính thể tích V của hình lập phương có cạnh bằng a là: \(V = {a^3}\). Do đó, \(a = \sqrt[3]{V}\).
Trả lời câu hỏi Vận dụng 2 trang 69SGK Toán 9 Cùng khám phá
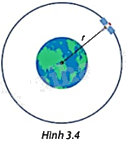
Bán kính r(m) của quỹ đạo của một vệ tinh (giả sử quỹ đạo của vệ tinh là đường tròn) được ước tính bởi công thức \(r = \sqrt[3]{{\frac{{GM{t^2}}}{{4{\pi ^2}}}}}\), trong đó \(G\left( {N{m^2}/k{g^2}} \right)\) là hằng số hấp dẫn vũ trụ, M(kg) là khối lượng của Trái Đất và t(s) là thời gian để vệ tinh hoàn thành một quỹ đạo (nguồn: http://courses.lumenlearning.com/suny-osuniversityphysics/chapter/13-4-satellite-orbits-and-energy/). Hãy ước tính bán kính của quỹ đạo của vệ tinh có thời gian hoàn thành một quỹ đạo là \(2,{6.10^6}\) giây, biết rằng \(G = \frac{{6,67}}{{{{10}^{11}}}}\left( {N{m^2}/k{g^2}} \right)\) và \(M = 5,{98.10^{24}}\left( {kg} \right)\) (làm tròn kết quả đến hàng nghìn).
Phương pháp giải:
Căn bậc ba của một số thực a là số x sao cho \({x^3} = a\).
Lời giải chi tiết:
Thay \(G = \frac{{6,67}}{{{{10}^{11}}}},M = 5,{98.10^{24}},t = 2,{6.10^6}\) thay vào công thức \(r = \sqrt[3]{{\frac{{GM{t^2}}}{{4{\pi ^2}}}}}\) ta có:
\(r = \sqrt[3]{{\frac{{\frac{{6,67}}{{{{10}^{11}}}}.5,{{98.10}^{24}}.{{\left( {2,{{6.10}^6}} \right)}^2}}}{{4{\pi ^2}}}}} \approx 408\;763\;000\).
Trả lời câu hỏi Hoạt động 2 trang 68 SGK Toán 9 Cùng khám phá
Tìm công thức tính thể tích V của hình lập phương có cạnh bằng a. Từ đó giải thích vì sao \(a = \sqrt[3]{V}\).
Phương pháp giải:
Sử dụng công thức tính thể tích V của hình lập phương.
Lời giải chi tiết:
Công thức tính thể tích V của hình lập phương có cạnh bằng a là: \(V = {a^3}\). Do đó, \(a = \sqrt[3]{V}\).
Trả lời câu hỏi Vận dụng 2 trang 69SGK Toán 9 Cùng khám phá
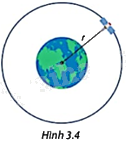
Bán kính r(m) của quỹ đạo của một vệ tinh (giả sử quỹ đạo của vệ tinh là đường tròn) được ước tính bởi công thức \(r = \sqrt[3]{{\frac{{GM{t^2}}}{{4{\pi ^2}}}}}\), trong đó \(G\left( {N{m^2}/k{g^2}} \right)\) là hằng số hấp dẫn vũ trụ, M(kg) là khối lượng của Trái Đất và t(s) là thời gian để vệ tinh hoàn thành một quỹ đạo (nguồn: http://courses.lumenlearning.com/suny-osuniversityphysics/chapter/13-4-satellite-orbits-and-energy/). Hãy ước tính bán kính của quỹ đạo của vệ tinh có thời gian hoàn thành một quỹ đạo là \(2,{6.10^6}\) giây, biết rằng \(G = \frac{{6,67}}{{{{10}^{11}}}}\left( {N{m^2}/k{g^2}} \right)\) và \(M = 5,{98.10^{24}}\left( {kg} \right)\) (làm tròn kết quả đến hàng nghìn).
Phương pháp giải:
Căn bậc ba của một số thực a là số x sao cho \({x^3} = a\).
Lời giải chi tiết:
Thay \(G = \frac{{6,67}}{{{{10}^{11}}}},M = 5,{98.10^{24}},t = 2,{6.10^6}\) thay vào công thức \(r = \sqrt[3]{{\frac{{GM{t^2}}}{{4{\pi ^2}}}}}\) ta có:
\(r = \sqrt[3]{{\frac{{\frac{{6,67}}{{{{10}^{11}}}}.5,{{98.10}^{24}}.{{\left( {2,{{6.10}^6}} \right)}^2}}}{{4{\pi ^2}}}}} \approx 408\;763\;000\).
Mục 3 trang 68, 69 SGK Toán 9 tập 1 thuộc chương trình học về hàm số bậc nhất. Đây là một phần quan trọng trong chương trình Toán 9, đặt nền móng cho các kiến thức nâng cao hơn ở các lớp trên. Việc nắm vững kiến thức và kỹ năng giải các bài tập trong mục này là rất cần thiết để đạt kết quả tốt trong môn Toán.
Mục 3 tập trung vào các nội dung sau:
Để giải các bài tập trong Mục 3 trang 68, 69 SGK Toán 9 tập 1, các em cần nắm vững các kiến thức sau:
Lời giải:
...
Lời giải:
...
Lời giải:
...
Để giúp các em hiểu rõ hơn về các kiến thức và phương pháp giải bài tập trong Mục 3, chúng tôi xin đưa ra một số ví dụ minh họa và bài tập luyện tập:
Lời giải:
...
...
Khi học và giải bài tập về hàm số bậc nhất, các em cần lưu ý những điều sau:
Hy vọng rằng với bài giải chi tiết và các kiến thức, phương pháp giải bài tập được trình bày trong bài viết này, các em học sinh sẽ nắm vững kiến thức về hàm số bậc nhất và tự tin giải các bài tập trong Mục 3 trang 68, 69 SGK Toán 9 tập 1. Chúc các em học tập tốt!
| Bài tập | Lời giải |
|---|---|
| Bài 1 | ... |
| Bài 2 | ... |