Chào mừng bạn đến với bài học về Lý thuyết Phép quay Toán 9 tại giaitoan.edu.vn. Đây là một trong những kiến thức quan trọng giúp bạn hiểu sâu hơn về biến hình trong mặt phẳng. Bài viết này sẽ cung cấp đầy đủ lý thuyết, ví dụ minh họa và bài tập thực hành để bạn nắm vững kiến thức này.
Chúng tôi cam kết mang đến cho bạn trải nghiệm học toán online hiệu quả và thú vị.
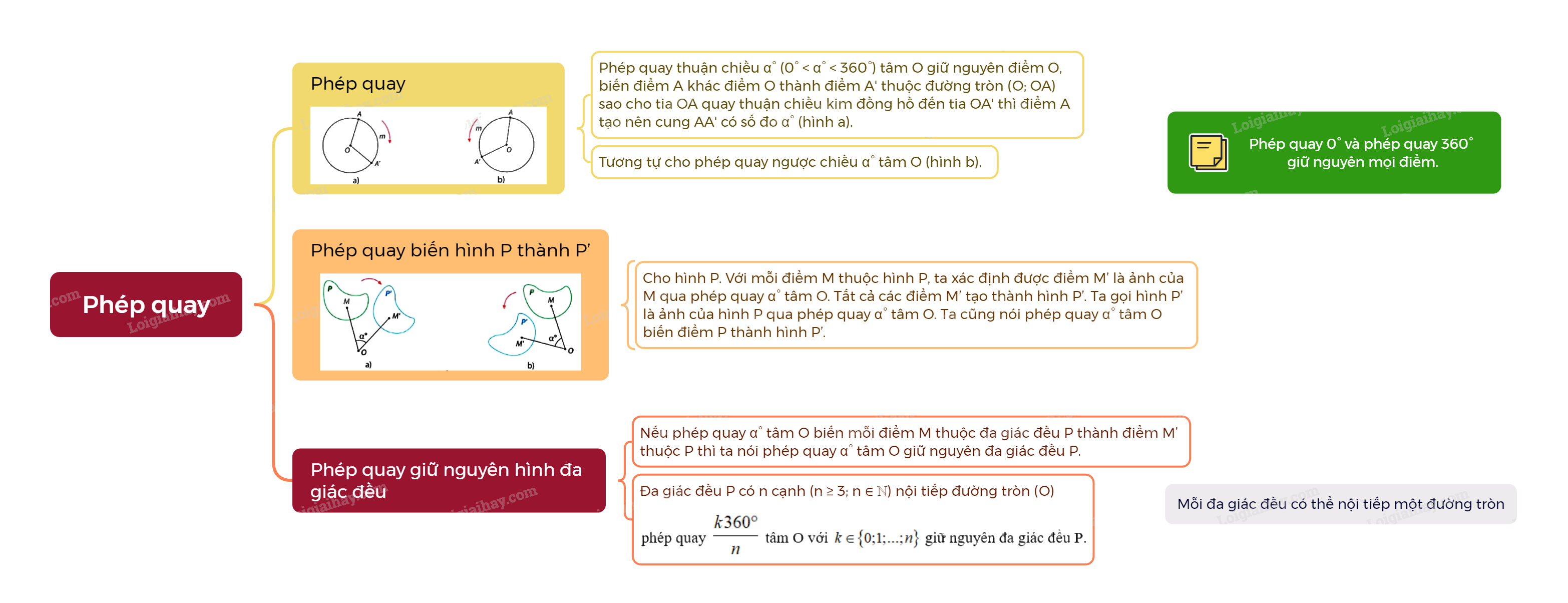
Khái niệm phép quay Phép quay thuận chiều (alpha ^circ ) (0° < (alpha ^circ ) < 360°) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm A’ thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AmA’ có số đo (alpha ^circ ) (hình a).
Khái niệm phép quay
Phép quay thuận chiều \(\alpha ^\circ \) (0° < \(\alpha ^\circ \) < 360°) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm A’ thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AmA’ có số đo \(\alpha ^\circ \) (hình a). Định nghĩa tương tự cho phép quay ngược chiều \(\alpha ^\circ \) tâm O (hình b). Chú ý: Phép quay 0° và phép quay 360° giữ nguyên mọi điểm.
Nếu phép quay \(\alpha ^\circ \) tâm O biến điểm A thành điểm A’ thì điểm A’ được gọi là ảnh của điểm A qua phép quay này. |
Phép quay biến hình P thành P’
Cho hình P. Với mỗi điểm M thuộc hình P, ta xác định được điểm M’ là ảnh của M qua phép quay \(\alpha ^\circ \) tâm O. Tất cả các điểm M’ tạo thành hình P’. Ta gọi hình P’ là ảnh của hình P qua phép quay \(\alpha ^\circ \) tâm O. Ta cũng nói phép quay \(\alpha ^\circ \) tâm O biến điểm P thành hình P’.
|
Phép quay giữ nguyên đa giác đều
Nếu phép quay \(\alpha ^\circ \) tâm O biến mỗi điểm M thuộc đa giác đều P thành điểm M’ thuộc P thì ta nói phép quay \(\alpha ^\circ \) tâm O giữ nguyên đa giác đều P. |
Lưu ý: Người ta chứng minh được rằng mỗi đa giác đều có thể nội tiếp một đường tròn. Cho đa giác đều P có n cạnh (\(n \in \mathbb{R},n \ge 3\)) nội tiếp đường tròn (O), phép quay \(\frac{{k360^\circ }}{n}\) tâm O với \(k \in \left\{ {0;1;...;n} \right\}\) giữ nguyên đa giác đều P.
Ví dụ:
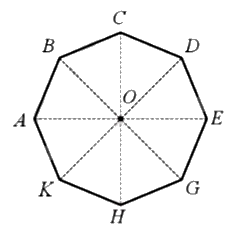
Ta có AB = BC = CD = DE = EG = GH = HK = KA nên số đo các cung nhỏ AB, BC, CD, DE, EG, GH, HK, KA đều bằng \(\frac{{360^\circ }}{8} = 45^\circ \).
Các phép quay thuận chiều (hoặc ngược chiều) \(45^\circ ,90^\circ ,135^\circ ,180^\circ ,225^\circ ,270^\circ ,315^\circ \) tâm O giữ nguyên bát giác ABCDEGHK.
Phép quay là một phép biến hình quan trọng trong hình học, giúp chúng ta hiểu rõ hơn về sự biến đổi của các hình trong mặt phẳng. Trong chương trình Toán 9, việc nắm vững lý thuyết phép quay là nền tảng để giải quyết các bài toán liên quan đến biến hình, đối xứng và các ứng dụng thực tế.
Phép quay tâm O với góc quay α (α đo bằng độ, thường từ 0 đến 360) là phép biến hình biến mỗi điểm M thành điểm M' sao cho:
Trong đó:
Phép quay có những tính chất quan trọng sau:
Giả sử trong mặt phẳng tọa độ Oxy, ta có điểm M(x; y) và tâm quay O(0; 0). Khi quay điểm M một góc α quanh O, ta được điểm M'(x'; y') có tọa độ:
x' = x*cos(α) - y*sin(α)
y' = x*sin(α) + y*cos(α)
Nếu tâm quay không phải là gốc tọa độ O(a; b), công thức tọa độ sẽ phức tạp hơn, cần thực hiện phép tịnh tiến về gốc tọa độ trước khi áp dụng công thức trên.
Phép quay có nhiều ứng dụng trong thực tế và trong các lĩnh vực khác nhau:
Để hiểu rõ hơn về lý thuyết phép quay, chúng ta hãy cùng giải một số bài tập sau:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về Lý thuyết Phép quay Toán 9. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!