Chào mừng các em học sinh đến với bài giải bài tập 5.21 trang 114 SGK Toán 9 tập 1 trên giaitoan.edu.vn. Bài tập này thuộc chương hàm số bậc nhất và ứng dụng, một trong những chủ đề quan trọng của chương trình Toán 9.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và áp dụng vào các bài tập tương tự.
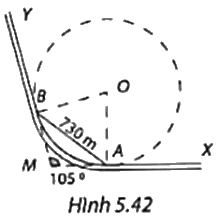
Trong Hình 5.42, để tàu không trật bánh ray khi chuyển hướng từ đường ray thẳng XA sang đường ray thẳng YB, đoạn ray nối được thiết kế là một phần của đường tròn (O) tiếp xúc với XA tại A và BY tại B. Biết góc chuyển hướng của tàu là \(\widehat {AMB} = {105^o}\) và khoảng cách giữa hai điểm A và B là 730m. Tính bán kính của đường tròn (O). Làm tròn kết quả đến đơn vị mét.
Đề bài
Trong Hình 5.42, để tàu không trật bánh ray khi chuyển hướng từ đường ray thẳng XA sang đường ray thẳng YB, đoạn ray nối được thiết kế là một phần của đường tròn (O) tiếp xúc với XA tại A và BY tại B. Biết góc chuyển hướng của tàu là \(\widehat {AMB} = {105^o}\) và khoảng cách giữa hai điểm A và B là 730m. Tính bán kính của đường tròn (O). Làm tròn kết quả đến đơn vị mét.
Phương pháp giải - Xem chi tiết
+ Sử dụng tính chất hai tiếp tuyến cắt nhau suy ra \(MA = MB\), \(\widehat {AMO} = \widehat {BMO} = \frac{1}{2}\widehat {BMA}\).
+ Chứng minh MO là đường trung trực của AB.
+ Gọi I là trung điểm của AB thì \(AI = \frac{{AB}}{2}\) và MO vuông góc với AB tại I.
+ Chứng minh tam giác MAO vuông tại A, tính góc MOA.
+ Tam giác AIO vuông tại I nên \(AI = AO.\sin IOA\), từ đó tính được AO.
Lời giải chi tiết
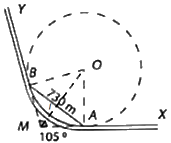
Vì MA, MB là tiếp tuyến của (O) nên:
+ \(MA = MB\).
+ MO là tia phân giác góc BMA nên
\(\widehat {AMO} = \widehat {BMO} = \frac{1}{2}\widehat {BMA} = 52,{5^o}\).
Vì \(OA = OB\) (bán kính (O)) nên O thuộc đường trung trực của AB.
Vì \(MA = MB\) nên M thuộc đường trung trực của AB.
Do đó, MO là đường trung trực của AB.
Gọi I là trung điểm của AB thì \(AI = \frac{{730}}{2} = 365\left( m \right)\) và MO vuông góc với AB tại I.
Vì MA là tiếp tuyến của (O) nên \(MA \bot AO\)
Suy ra, tam giác MOA vuông tại A nên \(\widehat {MOA} = {90^o} - \widehat {AMO} = 37,{5^o}\)
Tam giác AIO vuông tại I nên \(AI = AO.\sin IOA\),
suy ra \(AO = \frac{{AI}}{{\sin IOA}} = \frac{{365}}{{\sin 37,{5^o}}} \approx 600\left( m \right)\).
Vậy bán kính đường tròn (O) khoảng 600m.
Bài tập 5.21 trang 114 SGK Toán 9 tập 1 yêu cầu chúng ta tìm hiểu về phương pháp tiếp tuyến của một đường thẳng với một đường tròn. Đây là một kiến thức quan trọng trong hình học, giúp chúng ta hiểu rõ hơn về mối quan hệ giữa đường thẳng và đường tròn.
Để giải bài tập 5.21, chúng ta cần xác định được các yếu tố sau:
(Giả sử bài tập 5.21 có nội dung cụ thể về một bài toán hình học liên quan đến tiếp tuyến của đường tròn. Phần này sẽ trình bày lời giải chi tiết dựa trên nội dung bài toán đó. Ví dụ:)
Cho đường tròn (O; 5cm) và đường thẳng d cách O một khoảng 3cm. Chứng minh rằng đường thẳng d không phải là tiếp tuyến của đường tròn (O).
Lời giải:
Gọi H là hình chiếu vuông góc của O lên đường thẳng d. Khi đó, OH = 3cm.
Vì OH < bán kính R = 5cm nên đường thẳng d cắt đường tròn (O) tại hai điểm phân biệt. Do đó, đường thẳng d không phải là tiếp tuyến của đường tròn (O).
Để củng cố kiến thức về phương pháp tiếp tuyến, các em có thể tham khảo và giải các bài tập tương tự sau:
Kiến thức về tiếp tuyến của đường tròn có nhiều ứng dụng trong thực tế, ví dụ như:
Bài tập 5.21 trang 114 SGK Toán 9 tập 1 là một bài tập quan trọng giúp các em hiểu rõ hơn về phương pháp tiếp tuyến của đường tròn. Hy vọng với lời giải chi tiết và các bài tập luyện tập trên, các em sẽ nắm vững kiến thức này và áp dụng thành công vào các bài toán khác.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!