Chào mừng các em học sinh đến với bài giải bài tập 9.12 trang 83 SGK Toán 9 tập 2 trên giaitoan.edu.vn. Bài tập này thuộc chương hàm số bậc nhất và ứng dụng, một trong những chủ đề quan trọng của chương trình Toán 9.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán. Đồng thời, chúng tôi cũng có các bài giảng video và bài tập luyện tập để các em củng cố kiến thức đã học.
Tính khối lượng thép cần dùng để sản xuất 1000 chiếc đinh tán có thân hình trụ và đầu là nửa hình cầu với kích thước như Hình 9.47, biết khối lượng riêng của thép là 7850 kg/m3.
Đề bài
Tính khối lượng thép cần dùng để sản xuất 1000 chiếc đinh tán có thân hình trụ và đầu là nửa hình cầu với kích thước như Hình 9.47, biết khối lượng riêng của thép là 7850 kg/m3.
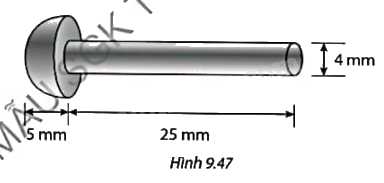
Phương pháp giải - Xem chi tiết
Thể tích của hình trụ: \(V = \pi {R^2}h\) (với R là bán kính đáy hình trụ, h là chiều cao)
Thể tích của hình cầu là: \(V = \frac{4}{3}\pi {R^3}\)(với R là bán kính hình cầu)
Khối lượng thép: m = V.D (D là khối lượng riêng)
Lời giải chi tiết
Thể tích phần hình trụ là:
\(V = \pi {R^2}h = \pi {.2^2}.25 = 100\pi \)(mm3)
Thể tích nửa hình cầu là:
\(V = \frac{4}{3}\pi {R^3} = \frac{{16}}{3}\pi \)(mm3)
Thể tích một chiếc đinh tán là:
\(100\pi + \frac{{16}}{3}\pi \approx 105\)(mm3)
Thể tích 1000 chiếc đinh tán là:
105.1000 = 105 000 (mm3) = 0,000105 (m3)
Suy ra khối lượng thép là:
m = D.V = 7850.0,000105 \( \approx \) 0,8 kg.
Bài tập 9.12 trang 83 SGK Toán 9 tập 2 yêu cầu học sinh vận dụng kiến thức về phương pháp tiếp tuyến để giải quyết một bài toán thực tế. Bài toán thường liên quan đến việc tìm phương trình tiếp tuyến của một đường cong tại một điểm cho trước, hoặc xác định điều kiện để một đường thẳng là tiếp tuyến của một đường cong.
Trước khi đi vào giải bài tập, chúng ta cần ôn lại một số kiến thức lý thuyết quan trọng:
Để giải bài tập 9.12 trang 83 SGK Toán 9 tập 2 một cách hiệu quả, chúng ta cần:
(Nội dung lời giải chi tiết sẽ được trình bày tại đây, bao gồm các bước giải cụ thể, các phép tính và giải thích rõ ràng. Ví dụ:)
Ví dụ: Giả sử bài toán yêu cầu tìm phương trình tiếp tuyến của đồ thị hàm số y = x2 tại điểm M(2; 4). Ta thực hiện như sau:
Để củng cố kiến thức và kỹ năng giải bài tập về phương pháp tiếp tuyến, các em có thể tham khảo các bài tập tương tự sau:
Phương pháp tiếp tuyến có nhiều ứng dụng trong thực tế, chẳng hạn như:
Bài tập 9.12 trang 83 SGK Toán 9 tập 2 là một bài tập quan trọng giúp các em hiểu sâu hơn về phương pháp tiếp tuyến và ứng dụng của nó. Hy vọng với lời giải chi tiết và các bài tập luyện tập trên giaitoan.edu.vn, các em sẽ nắm vững kiến thức và kỹ năng giải toán một cách hiệu quả.
| Khái niệm | Giải thích |
|---|---|
| Tiếp tuyến | Đường thẳng chỉ tiếp xúc với đồ thị hàm số tại một điểm. |
| Hệ số góc | Độ dốc của đường thẳng tiếp tuyến. |