Chào mừng các em học sinh đến với bài giải chi tiết mục 4 trang 66, 67 SGK Toán 9 tập 2 trên giaitoan.edu.vn. Chúng tôi cung cấp lời giải đầy đủ, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập Toán 9.
Bài học này tập trung vào các kiến thức quan trọng về... (nội dung cụ thể của mục 4 sẽ được điền vào đây khi có thông tin chi tiết về nội dung bài học)
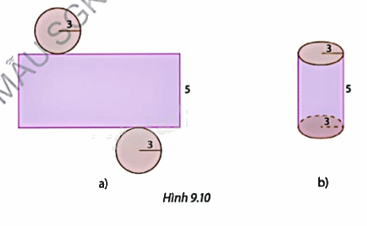
Tạo lập hình trụ có bán kính đáy 3 cm và chiều cao 5 cm theo các bước sau: Bước 1: Cắt hai miếng bìa hình tròn có bán kính bằng 3 cm và một miếng bìa hình chữ nhật có chiều rộng 5 cm, chiều dài bằng chu vi của miếng bìa hình tròn vừa cắt (Hình 9.10a) Bước 2: Dùng băng dính để dán các miếng bìa lại để được một hình trụ (Hình 9.10b).
Trả lời câu hỏi Luyện tập 4 trang 66SGK Toán 9 Cùng khám phá
Tạo lập hình trụ có bán kính đáy 2,5 cm và chiều cao 4 cm.
Phương pháp giải:
Tạo lập hình trụ có bán kính đáy 3 cm và chiều cao 5 cm theo các bước sau:
Bước 1: Cắt hai miếng bìa hình tròn có bán kính bằng 3 cm và một miếng bìa hình chữ nhật có chiều rộng 5 cm, chiều dài bằng chu vi của miếng bìa hình tròn vừa cắt.
Bước 2: Dùng băng dính để dán các miếng bìa lại để được một hình trụ.
Lời giải chi tiết:
HS tự thực hiện theo các bước trên.
Trả lời câu hỏi Vận dụng 3 trang 67 SGK Toán 9 Cùng khám phá
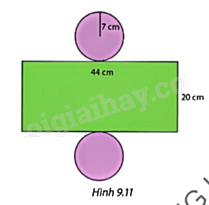
Tính diện tích xung quanh và thể tích của hình trụ có hình khai triển như Hình 9.11. Lấy \(\pi \approx \frac{{22}}{7}\).
Phương pháp giải:
Diện tích xung quanh hình trụ \({S_{xq}} = 2\pi rh\) (với r là bán kính đáy và h là chiều cao hình trụ).
Dựa vào thể tích hình trụ: V = \(\pi {r^2}h\) (với r là bán kính đáy và h là chiều cao hình trụ)
Lời giải chi tiết:
Diện tích xung quanh hình trụ là:
\({S_{xq}} = 2\pi rh = 2.\frac{{22}}{7}.7.20 = 880\)cm2.
Thể tích hình trụ là:
V = \(\pi {r^2}h = \frac{{22}}{7}{.7^2}.20 = 3080\)cm3.
Trả lời câu hỏi Hoạt động 4 trang 66 SGK Toán 9 Cùng khám phá
Tạo lập hình trụ có bán kính đáy 3 cm và chiều cao 5 cm theo các bước sau:
Bước 1: Cắt hai miếng bìa hình tròn có bán kính bằng 3 cm và một miếng bìa hình chữ nhật có chiều rộng 5 cm, chiều dài bằng chu vi của miếng bìa hình tròn vừa cắt (Hình 9.10a)
Bước 2: Dùng băng dính để dán các miếng bìa lại để được một hình trụ (Hình 9.10b).
Phương pháp giải:
Đọc kĩ dữ liệu đề bài và thực hành theo.
Lời giải chi tiết:
Trả lời câu hỏi Hoạt động 4 trang 66 SGK Toán 9 Cùng khám phá
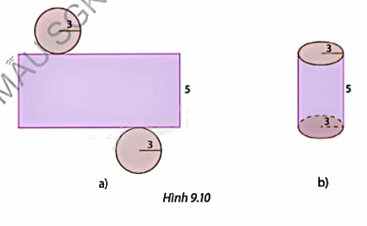
Tạo lập hình trụ có bán kính đáy 3 cm và chiều cao 5 cm theo các bước sau:
Bước 1: Cắt hai miếng bìa hình tròn có bán kính bằng 3 cm và một miếng bìa hình chữ nhật có chiều rộng 5 cm, chiều dài bằng chu vi của miếng bìa hình tròn vừa cắt (Hình 9.10a)
Bước 2: Dùng băng dính để dán các miếng bìa lại để được một hình trụ (Hình 9.10b).
Phương pháp giải:
Đọc kĩ dữ liệu đề bài và thực hành theo.
Lời giải chi tiết:
Trả lời câu hỏi Luyện tập 4 trang 66SGK Toán 9 Cùng khám phá
Tạo lập hình trụ có bán kính đáy 2,5 cm và chiều cao 4 cm.
Phương pháp giải:
Tạo lập hình trụ có bán kính đáy 3 cm và chiều cao 5 cm theo các bước sau:
Bước 1: Cắt hai miếng bìa hình tròn có bán kính bằng 3 cm và một miếng bìa hình chữ nhật có chiều rộng 5 cm, chiều dài bằng chu vi của miếng bìa hình tròn vừa cắt.
Bước 2: Dùng băng dính để dán các miếng bìa lại để được một hình trụ.
Lời giải chi tiết:
HS tự thực hiện theo các bước trên.
Trả lời câu hỏi Vận dụng 3 trang 67 SGK Toán 9 Cùng khám phá
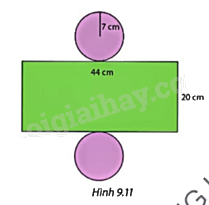
Tính diện tích xung quanh và thể tích của hình trụ có hình khai triển như Hình 9.11. Lấy \(\pi \approx \frac{{22}}{7}\).
Phương pháp giải:
Diện tích xung quanh hình trụ \({S_{xq}} = 2\pi rh\) (với r là bán kính đáy và h là chiều cao hình trụ).
Dựa vào thể tích hình trụ: V = \(\pi {r^2}h\) (với r là bán kính đáy và h là chiều cao hình trụ)
Lời giải chi tiết:
Diện tích xung quanh hình trụ là:
\({S_{xq}} = 2\pi rh = 2.\frac{{22}}{7}.7.20 = 880\)cm2.
Thể tích hình trụ là:
V = \(\pi {r^2}h = \frac{{22}}{7}{.7^2}.20 = 3080\)cm3.
Mục 4 trang 66, 67 SGK Toán 9 tập 2 thường xoay quanh các chủ đề về hàm số bậc nhất, hàm số bậc hai, hoặc các ứng dụng của chúng trong giải quyết bài toán thực tế. Việc nắm vững lý thuyết và phương pháp giải là yếu tố then chốt để hoàn thành tốt các bài tập trong mục này.
Trước khi đi vào giải bài tập, chúng ta cần ôn lại những kiến thức lý thuyết quan trọng sau:
Để giải các bài tập trong mục 4 trang 66, 67 SGK Toán 9 tập 2 một cách hiệu quả, chúng ta có thể áp dụng các phương pháp sau:
(Phần này sẽ chứa lời giải chi tiết cho từng bài tập trong mục 4 trang 66, 67 SGK Toán 9 tập 2. Ví dụ:)
Đề bài: ...
Lời giải: ...
Đề bài: ...
Lời giải: ...
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 9 tập 2 hoặc trên các trang web học toán online khác. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và tự tin hơn khi làm bài kiểm tra.
Trong quá trình giải bài tập, các em cần chú ý:
Hy vọng với bài giải chi tiết này, các em sẽ hiểu rõ hơn về mục 4 trang 66, 67 SGK Toán 9 tập 2 và tự tin hơn trong việc học tập môn Toán.