Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 1 trang 111 và 112 sách giáo khoa Toán 9 tập 1.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài toán, nắm vững phương pháp giải và tự tin làm bài tập. Hãy cùng bắt đầu nhé!
Trong Hình 5.30, đường thẳng a tiếp xúc với đường tròn (O; R) tại A và H là chân đường vuông góc kẻ từ O xuống a. Xác định độ dài OH. Vì sao A và H trùng nhau, nhận xét về góc tạo bởi tiếp tuyến a và bán kính OA.
Trả lời câu hỏi Hoạt động 1 trang 111SGK Toán 9 Cùng khám phá
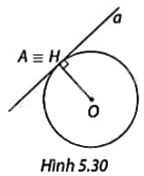
Trong Hình 5.30, đường thẳng a tiếp xúc với đường tròn (O; R) tại A và H là chân đường vuông góc kẻ từ O xuống a. Xác định độ dài OH. Vì sao A và H trùng nhau, nhận xét về góc tạo bởi tiếp tuyến a và bán kính OA.
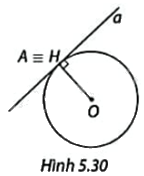
Phương pháp giải:
+ Chứng minh OH là khoảng cách từ O đến đường thẳng a. Mà đường thẳng a tiếp xúc với đường tròn (O; R) nên \(OH = R\).
+ Chứng minh \(OA = R\) và \(OA \bot a\) tại A, từ đó suy ra A và H trùng nhau.
+ Góc tạo bởi tiếp tuyến a và bán kính OA bằng \({90^o}\).
Lời giải chi tiết:
Vì H là chân đường vuông góc kẻ từ O xuống a nên OH là khoảng cách từ O đến đường thẳng a.
Mà đường thẳng a tiếp xúc với đường tròn (O; R) nên \(OH = R\).
Vì đường thẳng a tiếp xúc với đường tròn (O; R) tại A nên khoảng cách từ O đến đường thẳng a bằng bán kính đường tròn (O; R). Tức là: \(OA = R\) và \(OA \bot a\) tại A.
Do đó, A và H trùng nhau.
Góc tạo bởi tiếp tuyến a và bán kính OA bằng \({90^o}\).
Trả lời câu hỏi Hoạt động 2 trang 112 SGK Toán 9 Cùng khám phá
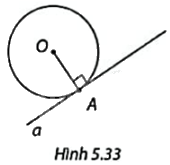
Trong Hình 5.33, đường tròn (O) có bán kính R và điểm A nằm trên đường tròn, đường thẳng a vuông góc với OA tại A. So sánh khoảng cách từ O đến đường thẳng a với bán kính R, từ đó xác định vị trí tương đối của a và (O).
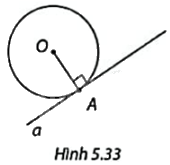
Phương pháp giải:
+ Chỉ ra \(OA = R\).
+ Chứng minh khoảng cách từ O đến đường thẳng a là: \(OA = R\).
+ Suy ra, đường thẳng a tiếp xúc với (O).
Lời giải chi tiết:
Vì A nằm trên đường tròn (O) nên \(OA = R\).
Vì đường thẳng a vuông góc với OA tại A nên khoảng cách từ O đến đường thẳng a là: \(OA = R\).
Do đó, đường thẳng a tiếp xúc với (O).
Trả lời câu hỏi Luyện tập 1 trang 111SGK Toán 9 Cùng khám phá
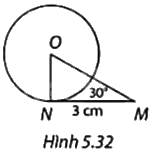
Trong Hình 5.32, MN là tiếp tuyến của đường tròn (O; R) tại N. Tính R.
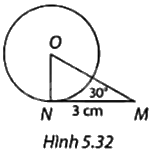
Phương pháp giải:
Chứng minh tam giác ONM vuông tại N, suy ra \(ON = NM.\tan M\)
Lời giải chi tiết:
Vì MN là tiếp tuyến của đường tròn (O; R) tại N nên \(ON \bot MN\). Do đó, tam giác ONM vuông tại N.
Suy ra \(ON = NM.\tan M = 3.\tan {30^o} = \sqrt 3 \)
Trả lời câu hỏi Luyện tập 2 trang 112 SGK Toán 9 Cùng khám phá
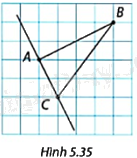
Trong Hình 5.35, cạnh mỗi hình vuông trong lưới ô vuông có độ dài là 1 đơn vị. Chứng minh rằng đường thẳng AC là tiếp tuyến của đường tròn tâm B, bán kính BA.
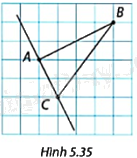
Phương pháp giải:
+ Sử dụng định lí Pythagore tính AB, BC, AC.
+ Sử dụng định lí Pythagore đảo chứng minh tam giác ABC vuông tại A, từ đó suy ra đường thẳng AC là tiếp tuyến của đường tròn tâm B, bán kính BA
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}A{B^2} = {2^2} + {4^2} = 20,\\B{C^2} = {3^2} + {4^2} = 25,\\A{C^2} = {1^2} + {2^2} = 5.\end{array}\)
Do đó, \(A{B^2} + A{C^2} = B{C^2}\) nên tam giác ABC vuông tại A. Suy ra, \(AB \bot AC\).
Suy ra, đường thẳng AC là tiếp tuyến của đường tròn tâm B, bán kính BA.
Trả lời câu hỏi Hoạt động 1 trang 111SGK Toán 9 Cùng khám phá
Trong Hình 5.30, đường thẳng a tiếp xúc với đường tròn (O; R) tại A và H là chân đường vuông góc kẻ từ O xuống a. Xác định độ dài OH. Vì sao A và H trùng nhau, nhận xét về góc tạo bởi tiếp tuyến a và bán kính OA.
Phương pháp giải:
+ Chứng minh OH là khoảng cách từ O đến đường thẳng a. Mà đường thẳng a tiếp xúc với đường tròn (O; R) nên \(OH = R\).
+ Chứng minh \(OA = R\) và \(OA \bot a\) tại A, từ đó suy ra A và H trùng nhau.
+ Góc tạo bởi tiếp tuyến a và bán kính OA bằng \({90^o}\).
Lời giải chi tiết:
Vì H là chân đường vuông góc kẻ từ O xuống a nên OH là khoảng cách từ O đến đường thẳng a.
Mà đường thẳng a tiếp xúc với đường tròn (O; R) nên \(OH = R\).
Vì đường thẳng a tiếp xúc với đường tròn (O; R) tại A nên khoảng cách từ O đến đường thẳng a bằng bán kính đường tròn (O; R). Tức là: \(OA = R\) và \(OA \bot a\) tại A.
Do đó, A và H trùng nhau.
Góc tạo bởi tiếp tuyến a và bán kính OA bằng \({90^o}\).
Trả lời câu hỏi Luyện tập 1 trang 111SGK Toán 9 Cùng khám phá
Trong Hình 5.32, MN là tiếp tuyến của đường tròn (O; R) tại N. Tính R.
Phương pháp giải:
Chứng minh tam giác ONM vuông tại N, suy ra \(ON = NM.\tan M\)
Lời giải chi tiết:
Vì MN là tiếp tuyến của đường tròn (O; R) tại N nên \(ON \bot MN\). Do đó, tam giác ONM vuông tại N.
Suy ra \(ON = NM.\tan M = 3.\tan {30^o} = \sqrt 3 \)
Trả lời câu hỏi Hoạt động 2 trang 112 SGK Toán 9 Cùng khám phá
Trong Hình 5.33, đường tròn (O) có bán kính R và điểm A nằm trên đường tròn, đường thẳng a vuông góc với OA tại A. So sánh khoảng cách từ O đến đường thẳng a với bán kính R, từ đó xác định vị trí tương đối của a và (O).
Phương pháp giải:
+ Chỉ ra \(OA = R\).
+ Chứng minh khoảng cách từ O đến đường thẳng a là: \(OA = R\).
+ Suy ra, đường thẳng a tiếp xúc với (O).
Lời giải chi tiết:
Vì A nằm trên đường tròn (O) nên \(OA = R\).
Vì đường thẳng a vuông góc với OA tại A nên khoảng cách từ O đến đường thẳng a là: \(OA = R\).
Do đó, đường thẳng a tiếp xúc với (O).
Trả lời câu hỏi Luyện tập 2 trang 112 SGK Toán 9 Cùng khám phá
Trong Hình 5.35, cạnh mỗi hình vuông trong lưới ô vuông có độ dài là 1 đơn vị. Chứng minh rằng đường thẳng AC là tiếp tuyến của đường tròn tâm B, bán kính BA.
Phương pháp giải:
+ Sử dụng định lí Pythagore tính AB, BC, AC.
+ Sử dụng định lí Pythagore đảo chứng minh tam giác ABC vuông tại A, từ đó suy ra đường thẳng AC là tiếp tuyến của đường tròn tâm B, bán kính BA
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}A{B^2} = {2^2} + {4^2} = 20,\\B{C^2} = {3^2} + {4^2} = 25,\\A{C^2} = {1^2} + {2^2} = 5.\end{array}\)
Do đó, \(A{B^2} + A{C^2} = B{C^2}\) nên tam giác ABC vuông tại A. Suy ra, \(AB \bot AC\).
Suy ra, đường thẳng AC là tiếp tuyến của đường tròn tâm B, bán kính BA.
Mục 1 của chương trình Toán 9 tập 1 thường tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc nhất. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài tập này thường yêu cầu học sinh xác định các yếu tố của hàm số bậc nhất (hệ số a, b), vẽ đồ thị hàm số, tìm giao điểm của đồ thị hàm số với các trục tọa độ, và giải các bài toán liên quan đến ứng dụng của hàm số bậc nhất.
Ví dụ:
Bài tập này yêu cầu học sinh vận dụng các phương pháp giải hệ phương trình bậc nhất hai ẩn (phương pháp thế, phương pháp cộng đại số) để tìm nghiệm của hệ phương trình. Các bài toán thường được đặt trong các tình huống thực tế để tăng tính ứng dụng.
Ví dụ:
Giải hệ phương trình sau:
{
Bài tập này yêu cầu học sinh xây dựng mô hình toán học từ các bài toán thực tế, sử dụng hàm số bậc nhất và hệ phương trình bậc nhất hai ẩn để giải quyết bài toán, và diễn giải kết quả.
Ví dụ:
Một người đi xe máy từ A đến B với vận tốc 40km/h. Sau khi đi được 1 giờ, người đó tăng vận tốc lên 50km/h và đến B muộn hơn 30 phút so với dự kiến. Tính quãng đường AB.
Ngoài sách giáo khoa, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng với những hướng dẫn chi tiết trên, các em sẽ tự tin giải quyết các bài tập trong mục 1 trang 111, 112 SGK Toán 9 tập 1. Chúc các em học tập tốt!