Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Chúng tôi giúp bạn nắm vững kiến thức và tự tin giải quyết mọi bài toán. Bài viết này sẽ hướng dẫn bạn giải mục 1 trang 123 SGK Toán 9 tập 1 một cách nhanh chóng và hiệu quả.
Quan sát hình ngôi sao năm cánh trong Hình 5.60, đỉnh và cạnh của góc CAD có liên hệ như thế nào với đường tròn khung của lồng đèn ông sao?
Trả lời câu hỏi Hoạt động 1 trang 123SGK Toán 9 Cùng khám phá
Quan sát hình ngôi sao năm cánh trong Hình 5.60, đỉnh và cạnh của góc CAD có liên hệ như thế nào với đường tròn khung của lồng đèn ông sao?
Phương pháp giải:
Quan sát hình và đưa ra nhận xét.
Lời giải chi tiết:
Góc CAD có đỉnh A nằm trên đường tròn (O), hai cạnh AC, AD là hai dây của đường tròn (O).
Trả lời câu hỏi Luyện tập 1 trang 123SGK Toán 9 Cùng khám phá
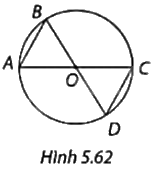
Viết tên các góc nội tiếp của đường tròn (O) được vẽ trong Hình 5.62.
Phương pháp giải:
Góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây của đường tròn được gọi là một góc nội tiếp của đường tròn.
Lời giải chi tiết:
Các góc nội tiếp của đường tròn (O) là: \(\widehat {CAB},\widehat {ABD},\widehat {ACD},\widehat {BDC}\).
Trả lời câu hỏi Hoạt động 1 trang 123SGK Toán 9 Cùng khám phá
Quan sát hình ngôi sao năm cánh trong Hình 5.60, đỉnh và cạnh của góc CAD có liên hệ như thế nào với đường tròn khung của lồng đèn ông sao?
Phương pháp giải:
Quan sát hình và đưa ra nhận xét.
Lời giải chi tiết:
Góc CAD có đỉnh A nằm trên đường tròn (O), hai cạnh AC, AD là hai dây của đường tròn (O).
Trả lời câu hỏi Luyện tập 1 trang 123SGK Toán 9 Cùng khám phá
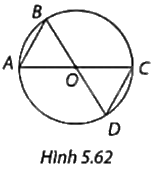
Viết tên các góc nội tiếp của đường tròn (O) được vẽ trong Hình 5.62.
Phương pháp giải:
Góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây của đường tròn được gọi là một góc nội tiếp của đường tròn.
Lời giải chi tiết:
Các góc nội tiếp của đường tròn (O) là: \(\widehat {CAB},\widehat {ABD},\widehat {ACD},\widehat {BDC}\).
Mục 1 trang 123 SGK Toán 9 tập 1 thường xoay quanh các chủ đề về hàm số bậc nhất, hệ số góc, và ứng dụng của hàm số trong việc giải quyết các bài toán thực tế. Việc nắm vững kiến thức nền tảng về hàm số là vô cùng quan trọng, không chỉ cho việc học Toán 9 mà còn là bước đệm cho các kiến thức nâng cao hơn ở các lớp trên.
Mục 1 thường bao gồm các bài tập sau:
Để xác định một hàm số có phải là hàm số bậc nhất hay không, ta cần kiểm tra xem nó có dạng y = ax + b hay không, với a và b là các số thực và a ≠ 0. Hệ số góc của hàm số bậc nhất là a. Nếu a > 0, hàm số đồng biến; nếu a < 0, hàm số nghịch biến.
Ví dụ:
Cho hàm số y = 2x - 3. Đây là hàm số bậc nhất vì nó có dạng y = ax + b, với a = 2 và b = -3. Hệ số góc của hàm số là 2, do đó hàm số đồng biến.
Để vẽ đồ thị hàm số bậc nhất y = ax + b, ta thực hiện các bước sau:
Ví dụ:
Vẽ đồ thị hàm số y = -x + 1.
Chọn điểm A(0; 1) và điểm B(1; 0). Vẽ đường thẳng đi qua hai điểm A và B. Đó là đồ thị của hàm số y = -x + 1.
Để tìm giao điểm của hai đường thẳng y = a1x + b1 và y = a2x + b2, ta giải hệ phương trình sau:
{ y = a1x + b1y = a2x + b2 }
Nghiệm của hệ phương trình là tọa độ giao điểm của hai đường thẳng.
Ví dụ:
Tìm giao điểm của hai đường thẳng y = 2x - 1 và y = -x + 2.
Giải hệ phương trình:
{ y = 2x - 1y = -x + 2 }
Ta có: 2x - 1 = -x + 2 => 3x = 3 => x = 1. Thay x = 1 vào phương trình y = 2x - 1, ta được y = 2(1) - 1 = 1. Vậy giao điểm của hai đường thẳng là (1; 1).
Hàm số bậc nhất được ứng dụng rộng rãi trong việc giải quyết các bài toán thực tế, ví dụ như tính tiền điện, tính quãng đường đi được, tính lợi nhuận,...
Ví dụ:
Một người đi xe máy với vận tốc 40 km/h. Hỏi sau 2 giờ người đó đi được quãng đường bao nhiêu?
Gọi x là thời gian đi (giờ) và y là quãng đường đi được (km). Ta có hàm số y = 40x. Thay x = 2 vào hàm số, ta được y = 40(2) = 80. Vậy sau 2 giờ người đó đi được quãng đường 80 km.
Hy vọng với hướng dẫn chi tiết này, bạn sẽ tự tin giải quyết các bài tập trong Mục 1 trang 123 SGK Toán 9 tập 1. Chúc bạn học tốt!