Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 3 trang 40, 41, 42 của sách giáo khoa Toán 9 tập 1.
Mục tiêu của chúng ta là không chỉ tìm ra đáp án đúng mà còn hiểu rõ phương pháp giải, từ đó áp dụng vào các bài tập tương tự một cách hiệu quả.
Cho bất phương trình \(3x + 9 > 0\). a) Để vế trái của bất phương trình chỉ còn \(3x\), ta cộng vào hai vế số nào? Viết bất phương trình thu được sau khi cộng với số đó. b) Từ bất phương trình thu được ở câu a, làm thế nào để có một bất phương trình mà hệ số của ẩn bằng 1? Đó là bất phương trình nào?
Trả lời câu hỏi Hoạt động 4 trang 40SGK Toán 9 Cùng khám phá
Cho bất phương trình \(3x + 9 > 0\).
a) Để vế trái của bất phương trình chỉ còn \(3x\), ta cộng vào hai vế số nào? Viết bất phương trình thu được sau khi cộng với số đó.
b) Từ bất phương trình thu được ở câu a, làm thế nào để có một bất phương trình mà hệ số của ẩn bằng 1? Đó là bất phương trình nào?
Phương pháp giải:
Dựa vào các mối liên hệ giữa thứ tự và các phép toán để giải bài toán.
Lời giải chi tiết:
a) Để vế trái của bất phương trình chỉ còn \(3x\), ta cộng vào hai vế số \(\left( { - 9} \right)\). Bất phương trình thu được sau khi cộng là: \(3x > - 9\).
b) Từ bất phương trình thu được ở câu a, để có một bất phương trình mà hệ số của ẩn bằng 1 ta chia cả hai vế cho 3. Bất phương trình mới là: \(x > - 3\).
Trả lời câu hỏi Luyện tập 5 trang 42 SGK Toán 9 Cùng khám phá
Giải các bất phương trình sau:
a) \( - 3x - 2 > 4x + 7\).
b) \(\frac{7}{3}x - 3 \le 1 - 4x\).
Phương pháp giải:
Sử dụng ba bước giải bất phương trình để giải bài toán.
Lời giải chi tiết:
a) \( - 3x - 2 > 4x + 7\)
\(\begin{array}{l} - 3x - 4x > 7 + 2\\ - 7x > 9\\x < \frac{{ - 9}}{7}.\end{array}\)
Vậy nghiệm của bất phương trình là \(x < \frac{{ - 9}}{7}\).
b) \(\frac{7}{3}x - 3 \le 1 - 4x\)
\(\begin{array}{l}\frac{7}{3}x + 4x \le 1 + 3\\\frac{{19}}{3}x \le 4\\x \le \frac{{12}}{{19}}.\end{array}\)
Vậy nghiệm của bất phương trình là \(x \le \frac{{12}}{{19}}\).
Trả lời câu hỏi Luyện tập 4 trang 41 SGK Toán 9 Cùng khám phá
Giải các bất phương trình sau:
a) \(4x - 9 \ge 0\);
b) \(0,3 - 0,2x < 0\).
Phương pháp giải:
Sử dụng ba bước giải bất phương trình để giải bài toán.
Lời giải chi tiết:
a) \(4x - 9 \ge 0\)
\(\begin{array}{l}4x \ge 9\\4x:4 \ge 9:4\\x \ge \frac{9}{4}.\end{array}\)
Vậy nghiệm của bất phương trình là \(x \ge \frac{9}{4}\).
b) \(0,3 - 0,2x < 0\)
\(\begin{array}{l} - 0,2x < - 0,3\\ - 0,2x:\left( { - 0,2} \right) < \left( { - 0,3} \right):\left( { - 0,2} \right)\\x > 1,5.\end{array}\)
Vậy nghiệm của bất phương trình là \(x > 1,5\)
Trả lời câu hỏi Luyện tập 6 trang 43 SGK Toán 9 Cùng khám phá
Bác sĩ khuyên cô Vân mỗi ngày ăn không quá 60 gam chất béo. Hôm nay, theo tính toán của cô Vân về lượng chất béo đã ăn thì bữa điểm tâm sáng là 8 gam, bữa trưa là 31 gam. Nếu tuân thủ lời khuyên của bác sĩ thì cô Vân có thể ăn nhiều nhất là bao nhiêu gam chất béo trong thời gian còn lại của ngày?
Phương pháp giải:
Dựa vào cách giải bất phương trình để giải bài toán.
Lời giải chi tiết:
Gọi \(x\) là số gam chất béo trong thời gian còn lại của ngày.
Nếu muốn tuân thủ lời khuyên của bác sĩ thì số gam chất béo trong thời gian còn lại của ngày phải thỏa mãn điều kiện: \(x + 8 + 31 \le 60\).
Đây là một bất phương trình ẩn \(x\). Giải bất phương trình để tìm \(x\). Ta có:
\(\begin{array}{l}x + 8 + 31 \le 60\\x + 39 \le 60\\x \le 60 - 39\\x \le 21.\end{array}\)
Vậy cô Vân có thể ăn nhiều nhất là 21 gam chất béo trong thời gian còn lại của ngày.
Trả lời câu hỏi Vận dụng 2 trang 43SGK Toán 9 Cùng khám phá
Trò chơi chọn số
Cô giáo đưa ra hai cách tìm số mới từ một số \(x\) được chọn ngẫu nhiên.
+ Cách A: Lấy \(x\) nhân với 3, được bao nhiêu đem cộng thêm 50.
+ Cách B: Lấy \(x\) trừ đi 1, được bao nhiêu đem nhân với 5.
Có hai đội chơi: Đội chọn cách A gọi là đội A, đội chọn cách B gọi là đội B.
Luật chơi:
Đội đi trước được quyền chọn số. Sau khi thảo luận để chọn một giá trị của \(x\), đội chọn số thông báo số đã chọn. Với số \(x\) đã được thông báo, mỗi đội sử dụng cách tính số của mình và cho biết kết quả.
Nếu kết quả của đội chọn số lớn hơn kết quả của đối thủ thì đội chọn số thẳng và được quyền chọn tiếp một giá trị khác của \(x\).
Trong trường hợp kết quả của đội chọn số nhỏ hơn hoặc bằng kết quả của đối thủ thì đội chọn số thua và phải nhường lượt chơi cho đối thủ.
Nếu đội A được quyền chọn số thì nên chọn như thế nào để đảm bảo thắng?
Nếu đội B được quyền chọn số thì nên chọn như thế nào để đảm bảo thắng?
Phương pháp giải:
Dựa vào cách giải bất phương trình để đưa ra cách chọn cho từng đội.
Lời giải chi tiết:
Cách chọn A có biểu thức: \(3x + 50\).
Cách chọn B có biểu thức: \(\left( {x - 1} \right).5\).
Nếu đội A được quyền chọn số thì cách chọn để đội A đảm bảo thắng là:
\(\begin{array}{l}3x + 50 > \left( {x - 1} \right).5\\3x + 50 > 5x - 5\\3x - 5x > - 50 - 5\\ - 2x > - 55\\x < \frac{{55}}{2}.\end{array}\)
Vậy nếu đội A được quyền chọn số thì đội A cần chọn số nhỏ hơn 25,5 để đảm bảo thắng.
Nếu đội B được quyền chọn số thì cách chọn để đội B đảm bảo thắng là:
\(\begin{array}{l}5\left( {x - 1} \right) > 3x + 50\\5x - 5 > 3x + 50\\5x - 3x > 50 + 5\\2x > 55\\x > \frac{{55}}{2}.\end{array}\)
Vậy nếu đội B được quyền chọn số thì đọi B cần chọn số lớn hơn 25,5 để đảm bảo thắng.
Trả lời câu hỏi Vận dụng 1 trang 43 SGK Toán 9 Cùng khám phá
Trở lại với bài toán nêu ở đầu bài học.
Chủ đầu tư khu chung cư Vạn Xuân muốn quy hoạch khu đất hình chữ nhật kích thước \(50m \times 75m\) giữa các tòa nhà bằng cách chia nó thành ba hình chữ nhật nhỏ A, B, C như Hình 2.3. Phần A dùng để làm sân tập luyện thể thao (có thể chơi bóng rổ, bóng chuyền), phần B dành để trồng cây xanh và phần C là nơi đặt cầu trượt, bập bênh cho trẻ em. Chủ đầu tư muốn chia khu đất sao cho diện tích hình A không nhỏ hơn diện tích hình B.
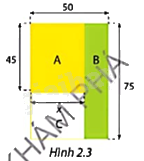
Hãy giúp chủ đầu tư khu chung cư Vạn Xuân xác định cạnh \(x\) của hình chữ nhật A.
Phương pháp giải:
Dựa vào cách giải bất phương trình để giải bài toán.
Lời giải chi tiết:
Diện tích hình chữ nhật A là: \(45x\left( {{m^2}} \right)\).
Diện tích hình chữ nhật B là: \(75.\left( {50 - x} \right)\,\,\left( {{m^2}} \right)\).
Để diện tích hình A không nhỏ hơn diện tích hình B, ta có: \(45x \ge 75\left( {50 - x} \right)\).
Đây là một bất phương trình ẩn \(x\). Giải bất phương trình để tìm \(x\). Ta có:
\(\begin{array}{l}45x \ge 75\left( {50 - x} \right)\\45x \ge 3750 - 75x\\45x + 75x \ge 3750\\120x \ge 3750\\x \ge 31,25.\end{array}\)
Vậy để diện tích hình A không nhỏ hơn diện tích hình B thì độ dài cạnh \(x\) của hình chữ nhật A ít nhất phải bằng 31,25 (m).
Trả lời câu hỏi Hoạt động 5 trang 40 SGK Toán 9 Cùng khám phá
Hai bạn Trung và Mai thảo luận về hoạt động giải bất phương trình \( - 2x - 8 > 0\).
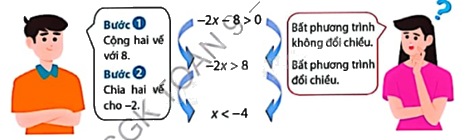
Bạn Mai hỏi bạn Trung: “Tại sao ở bước biến đổi thứ nhất, bất phương trình không đổi chiều? Còn ở bước biến đổi thứ hai thì bất phương trình lại đổi chiều?”
Em hãy giúp bạn Trung giải đáp thắc mắc của bạn Mai.
Phương pháp giải:
Dựa vào các mối liên hệ giữa thứ tự và các phép toán để giải bài toán.
Lời giải chi tiết:
+ Dựa vào mối liên hệ giữa thứ tự và phép cộng, thì ở bước thứ nhất không cần đổi chiều vì ta chỉ cộng một số vào hai vế.
+ Dựa vào mối liên hệ giữa thứ tự và phép nhân với số âm, thì ở bước thứ hai cần đổi chiều vì ta chia cho một số âm ở hai vế.
Trả lời câu hỏi Hoạt động 4 trang 40SGK Toán 9 Cùng khám phá
Cho bất phương trình \(3x + 9 > 0\).
a) Để vế trái của bất phương trình chỉ còn \(3x\), ta cộng vào hai vế số nào? Viết bất phương trình thu được sau khi cộng với số đó.
b) Từ bất phương trình thu được ở câu a, làm thế nào để có một bất phương trình mà hệ số của ẩn bằng 1? Đó là bất phương trình nào?
Phương pháp giải:
Dựa vào các mối liên hệ giữa thứ tự và các phép toán để giải bài toán.
Lời giải chi tiết:
a) Để vế trái của bất phương trình chỉ còn \(3x\), ta cộng vào hai vế số \(\left( { - 9} \right)\). Bất phương trình thu được sau khi cộng là: \(3x > - 9\).
b) Từ bất phương trình thu được ở câu a, để có một bất phương trình mà hệ số của ẩn bằng 1 ta chia cả hai vế cho 3. Bất phương trình mới là: \(x > - 3\).
Trả lời câu hỏi Hoạt động 5 trang 40 SGK Toán 9 Cùng khám phá
Hai bạn Trung và Mai thảo luận về hoạt động giải bất phương trình \( - 2x - 8 > 0\).
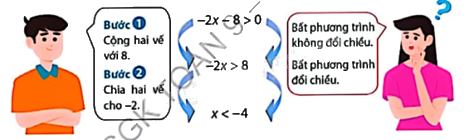
Bạn Mai hỏi bạn Trung: “Tại sao ở bước biến đổi thứ nhất, bất phương trình không đổi chiều? Còn ở bước biến đổi thứ hai thì bất phương trình lại đổi chiều?”
Em hãy giúp bạn Trung giải đáp thắc mắc của bạn Mai.
Phương pháp giải:
Dựa vào các mối liên hệ giữa thứ tự và các phép toán để giải bài toán.
Lời giải chi tiết:
+ Dựa vào mối liên hệ giữa thứ tự và phép cộng, thì ở bước thứ nhất không cần đổi chiều vì ta chỉ cộng một số vào hai vế.
+ Dựa vào mối liên hệ giữa thứ tự và phép nhân với số âm, thì ở bước thứ hai cần đổi chiều vì ta chia cho một số âm ở hai vế.
Trả lời câu hỏi Luyện tập 4 trang 41 SGK Toán 9 Cùng khám phá
Giải các bất phương trình sau:
a) \(4x - 9 \ge 0\);
b) \(0,3 - 0,2x < 0\).
Phương pháp giải:
Sử dụng ba bước giải bất phương trình để giải bài toán.
Lời giải chi tiết:
a) \(4x - 9 \ge 0\)
\(\begin{array}{l}4x \ge 9\\4x:4 \ge 9:4\\x \ge \frac{9}{4}.\end{array}\)
Vậy nghiệm của bất phương trình là \(x \ge \frac{9}{4}\).
b) \(0,3 - 0,2x < 0\)
\(\begin{array}{l} - 0,2x < - 0,3\\ - 0,2x:\left( { - 0,2} \right) < \left( { - 0,3} \right):\left( { - 0,2} \right)\\x > 1,5.\end{array}\)
Vậy nghiệm của bất phương trình là \(x > 1,5\)
Trả lời câu hỏi Luyện tập 5 trang 42 SGK Toán 9 Cùng khám phá
Giải các bất phương trình sau:
a) \( - 3x - 2 > 4x + 7\).
b) \(\frac{7}{3}x - 3 \le 1 - 4x\).
Phương pháp giải:
Sử dụng ba bước giải bất phương trình để giải bài toán.
Lời giải chi tiết:
a) \( - 3x - 2 > 4x + 7\)
\(\begin{array}{l} - 3x - 4x > 7 + 2\\ - 7x > 9\\x < \frac{{ - 9}}{7}.\end{array}\)
Vậy nghiệm của bất phương trình là \(x < \frac{{ - 9}}{7}\).
b) \(\frac{7}{3}x - 3 \le 1 - 4x\)
\(\begin{array}{l}\frac{7}{3}x + 4x \le 1 + 3\\\frac{{19}}{3}x \le 4\\x \le \frac{{12}}{{19}}.\end{array}\)
Vậy nghiệm của bất phương trình là \(x \le \frac{{12}}{{19}}\).
Trả lời câu hỏi Luyện tập 6 trang 43 SGK Toán 9 Cùng khám phá
Bác sĩ khuyên cô Vân mỗi ngày ăn không quá 60 gam chất béo. Hôm nay, theo tính toán của cô Vân về lượng chất béo đã ăn thì bữa điểm tâm sáng là 8 gam, bữa trưa là 31 gam. Nếu tuân thủ lời khuyên của bác sĩ thì cô Vân có thể ăn nhiều nhất là bao nhiêu gam chất béo trong thời gian còn lại của ngày?
Phương pháp giải:
Dựa vào cách giải bất phương trình để giải bài toán.
Lời giải chi tiết:
Gọi \(x\) là số gam chất béo trong thời gian còn lại của ngày.
Nếu muốn tuân thủ lời khuyên của bác sĩ thì số gam chất béo trong thời gian còn lại của ngày phải thỏa mãn điều kiện: \(x + 8 + 31 \le 60\).
Đây là một bất phương trình ẩn \(x\). Giải bất phương trình để tìm \(x\). Ta có:
\(\begin{array}{l}x + 8 + 31 \le 60\\x + 39 \le 60\\x \le 60 - 39\\x \le 21.\end{array}\)
Vậy cô Vân có thể ăn nhiều nhất là 21 gam chất béo trong thời gian còn lại của ngày.
Trả lời câu hỏi Vận dụng 1 trang 43 SGK Toán 9 Cùng khám phá
Trở lại với bài toán nêu ở đầu bài học.
Chủ đầu tư khu chung cư Vạn Xuân muốn quy hoạch khu đất hình chữ nhật kích thước \(50m \times 75m\) giữa các tòa nhà bằng cách chia nó thành ba hình chữ nhật nhỏ A, B, C như Hình 2.3. Phần A dùng để làm sân tập luyện thể thao (có thể chơi bóng rổ, bóng chuyền), phần B dành để trồng cây xanh và phần C là nơi đặt cầu trượt, bập bênh cho trẻ em. Chủ đầu tư muốn chia khu đất sao cho diện tích hình A không nhỏ hơn diện tích hình B.
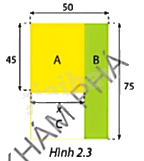
Hãy giúp chủ đầu tư khu chung cư Vạn Xuân xác định cạnh \(x\) của hình chữ nhật A.
Phương pháp giải:
Dựa vào cách giải bất phương trình để giải bài toán.
Lời giải chi tiết:
Diện tích hình chữ nhật A là: \(45x\left( {{m^2}} \right)\).
Diện tích hình chữ nhật B là: \(75.\left( {50 - x} \right)\,\,\left( {{m^2}} \right)\).
Để diện tích hình A không nhỏ hơn diện tích hình B, ta có: \(45x \ge 75\left( {50 - x} \right)\).
Đây là một bất phương trình ẩn \(x\). Giải bất phương trình để tìm \(x\). Ta có:
\(\begin{array}{l}45x \ge 75\left( {50 - x} \right)\\45x \ge 3750 - 75x\\45x + 75x \ge 3750\\120x \ge 3750\\x \ge 31,25.\end{array}\)
Vậy để diện tích hình A không nhỏ hơn diện tích hình B thì độ dài cạnh \(x\) của hình chữ nhật A ít nhất phải bằng 31,25 (m).
Trả lời câu hỏi Vận dụng 2 trang 43SGK Toán 9 Cùng khám phá
Trò chơi chọn số
Cô giáo đưa ra hai cách tìm số mới từ một số \(x\) được chọn ngẫu nhiên.
+ Cách A: Lấy \(x\) nhân với 3, được bao nhiêu đem cộng thêm 50.
+ Cách B: Lấy \(x\) trừ đi 1, được bao nhiêu đem nhân với 5.
Có hai đội chơi: Đội chọn cách A gọi là đội A, đội chọn cách B gọi là đội B.
Luật chơi:
Đội đi trước được quyền chọn số. Sau khi thảo luận để chọn một giá trị của \(x\), đội chọn số thông báo số đã chọn. Với số \(x\) đã được thông báo, mỗi đội sử dụng cách tính số của mình và cho biết kết quả.
Nếu kết quả của đội chọn số lớn hơn kết quả của đối thủ thì đội chọn số thẳng và được quyền chọn tiếp một giá trị khác của \(x\).
Trong trường hợp kết quả của đội chọn số nhỏ hơn hoặc bằng kết quả của đối thủ thì đội chọn số thua và phải nhường lượt chơi cho đối thủ.
Nếu đội A được quyền chọn số thì nên chọn như thế nào để đảm bảo thắng?
Nếu đội B được quyền chọn số thì nên chọn như thế nào để đảm bảo thắng?
Phương pháp giải:
Dựa vào cách giải bất phương trình để đưa ra cách chọn cho từng đội.
Lời giải chi tiết:
Cách chọn A có biểu thức: \(3x + 50\).
Cách chọn B có biểu thức: \(\left( {x - 1} \right).5\).
Nếu đội A được quyền chọn số thì cách chọn để đội A đảm bảo thắng là:
\(\begin{array}{l}3x + 50 > \left( {x - 1} \right).5\\3x + 50 > 5x - 5\\3x - 5x > - 50 - 5\\ - 2x > - 55\\x < \frac{{55}}{2}.\end{array}\)
Vậy nếu đội A được quyền chọn số thì đội A cần chọn số nhỏ hơn 25,5 để đảm bảo thắng.
Nếu đội B được quyền chọn số thì cách chọn để đội B đảm bảo thắng là:
\(\begin{array}{l}5\left( {x - 1} \right) > 3x + 50\\5x - 5 > 3x + 50\\5x - 3x > 50 + 5\\2x > 55\\x > \frac{{55}}{2}.\end{array}\)
Vậy nếu đội B được quyền chọn số thì đọi B cần chọn số lớn hơn 25,5 để đảm bảo thắng.
Mục 3 trong SGK Toán 9 tập 1 thường xoay quanh các chủ đề về hàm số bậc nhất, bao gồm định nghĩa, tính chất, đồ thị và ứng dụng của hàm số. Việc nắm vững kiến thức về hàm số bậc nhất là nền tảng quan trọng cho các chương trình học toán ở các lớp trên.
Bài tập này yêu cầu học sinh xác định các hệ số a, b trong hàm số y = ax + b dựa vào các thông tin cho trước, chẳng hạn như đồ thị, bảng giá trị hoặc các điểm thuộc đồ thị. Để giải bài tập này, học sinh cần nắm vững định nghĩa của hàm số bậc nhất và biết cách thay giá trị x, y vào phương trình để tìm a, b.
Để vẽ đồ thị hàm số bậc nhất, học sinh cần xác định ít nhất hai điểm thuộc đồ thị. Có thể chọn x = 0 để tìm y, hoặc chọn y = 0 để tìm x. Sau đó, nối hai điểm này lại với nhau để được đồ thị hàm số.
Để tìm giao điểm của hai đường thẳng, học sinh cần giải hệ phương trình bậc nhất hai ẩn, trong đó mỗi phương trình tương ứng với một đường thẳng. Nghiệm của hệ phương trình chính là tọa độ giao điểm của hai đường thẳng.
Các bài toán ứng dụng hàm số bậc nhất thường liên quan đến các tình huống thực tế như tính quãng đường, thời gian, chi phí,... Học sinh cần phân tích đề bài, xác định các đại lượng liên quan và xây dựng phương trình hàm số để giải quyết bài toán.
Ví dụ: Cho hàm số y = 2x - 1. Hãy tìm tọa độ giao điểm của đường thẳng này với đường thẳng y = x + 2.
Giải: Để tìm giao điểm, ta giải hệ phương trình:
y = 2x - 1
y = x + 2
Thay y = x + 2 vào phương trình đầu tiên, ta được: x + 2 = 2x - 1 => x = 3. Thay x = 3 vào phương trình y = x + 2, ta được: y = 5. Vậy tọa độ giao điểm là (3, 5).
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 9 tập 1 hoặc trên các trang web học toán online khác.
Hy vọng với bài viết này, các em học sinh đã nắm vững kiến thức và phương pháp giải các bài tập trong mục 3 trang 40, 41, 42 SGK Toán 9 tập 1. Chúc các em học tập tốt!