Chào mừng các em học sinh đến với bài giải chi tiết mục 4 trang 74, 75 SGK Toán 9 tập 2 trên giaitoan.edu.vn. Bài viết này sẽ cung cấp cho các em lời giải đầy đủ, chính xác và dễ hiểu cho từng bài tập trong mục, giúp các em củng cố kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, hỗ trợ tối đa cho các em học sinh trên con đường chinh phục môn Toán.
Bước 1: Cắt miếng bìa như Hình 9.27a rồi uốn miếng bìa lại và dán hai mép OA, OB sao cho chúng chồng khít lên nhau tạo thành mặt xung quanh của hình nón đỉnh O (không có đáy) như Hình 9.27b. Bước 2: Tính bán kính đáy r của hình nón tạo thành và cắt miếng bìa hình tròn bán kính r. Dùng băng dính dán miếng bìa này với mặt xung quanh của hình nón ở Bước 1 để tạo lập thành một hình nón.
Trả lời câu hỏi Luyện tập 4 trang 75 SGK Toán 9 Cùng khám phá
Tạo lập hình nón có bán kính đáy 5 cm và đường sinh 12 cm. Tính thể tích của hình nón vừa tạo lập.
Phương pháp giải:
Tính diện tích xung quanh hình nón, sau đó tính cung n và tạo lập theo các bước sau:
Cắt một miếng bìa hình quạt bán kính r giới hạn bởi cung 90o (một phần tư hình tròn bán kính r) và uốn miếng bìa tạo thành mặt xung quanh của hình nón.
Cắt một miếng bìa hình tròn bán kính r’ cm và dùng băng dính dán miếng bìa này với mặt xung quanh của hình nón vừa tạo.
Thể tích hình nón: \(V = \frac{1}{3}\pi {r^2}h\) (với r là bán kính đáy và h là chiều cao của hình nón).
Lời giải chi tiết:
Diện tích xung quanh của hình nón là:
\({S_{xq}} = \pi rn = \pi .5.12 = 60\pi \) cm2
Mặt xung quanh của hình nón trên là hình quạt tròn bán kính 12 cm giới hạn bởi cung no.
Ta có: \(\frac{{\pi {{.12}^2}.n}}{{360}} = 60\pi \) hay \(\frac{{2n}}{5} = 60\). Suy ra n = 150.
Từ đó, tạo lập hình nón trên theo các bước sau:
Cắt một miếng bìa hình quạt bán kính 12 cm giới hạn bởi cung 90o (một phần tư hình tròn bán kính 12 cm) và uốn miếng bìa tạo thành mặt xung quanh của hình nón.
Cắt một miếng bìa hình tròn bán kính 5 cm và dùng băng dính dán miếng bìa này với mặt xung quanh của hình nón vừa tạo.
Chiều cao của hình nón là:
\(\sqrt {{{12}^2} - {5^2}} = \sqrt {119} \) cm
Thể tích hình nón là:
\(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.5^2}\sqrt {119} \approx 285,6\) cm3.
Trả lời câu hỏi Hoạt động 4 trang 74 SGK Toán 9 Cùng khám phá
Bước 1: Cắt miếng bìa như Hình 9.27a rồi uốn miếng bìa lại và dán hai mép OA, OB sao cho chúng chồng khít lên nhau tạo thành mặt xung quanh của hình nón đỉnh O (không có đáy) như Hình 9.27b.
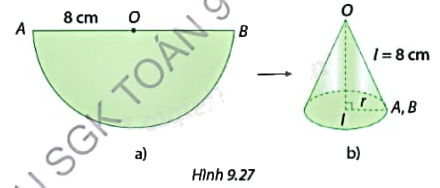
Bước 2: Tính bán kính đáy r của hình nón tạo thành và cắt miếng bìa hình tròn bán kính r. Dùng băng dính dán miếng bìa này với mặt xung quanh của hình nón ở Bước 1 để tạo lập thành một hình nón.
Phương pháp giải:
Đọc kĩ dữ kiện đề bài và làm theo.
Lời giải chi tiết:

Trả lời câu hỏi Hoạt động 4 trang 74 SGK Toán 9 Cùng khám phá
Bước 1: Cắt miếng bìa như Hình 9.27a rồi uốn miếng bìa lại và dán hai mép OA, OB sao cho chúng chồng khít lên nhau tạo thành mặt xung quanh của hình nón đỉnh O (không có đáy) như Hình 9.27b.
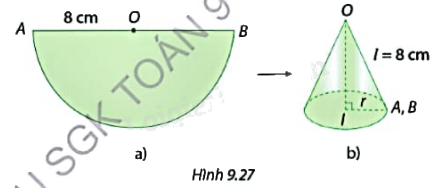
Bước 2: Tính bán kính đáy r của hình nón tạo thành và cắt miếng bìa hình tròn bán kính r. Dùng băng dính dán miếng bìa này với mặt xung quanh của hình nón ở Bước 1 để tạo lập thành một hình nón.
Phương pháp giải:
Đọc kĩ dữ kiện đề bài và làm theo.
Lời giải chi tiết:
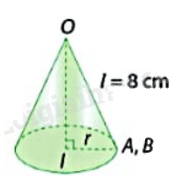
Trả lời câu hỏi Luyện tập 4 trang 75 SGK Toán 9 Cùng khám phá
Tạo lập hình nón có bán kính đáy 5 cm và đường sinh 12 cm. Tính thể tích của hình nón vừa tạo lập.
Phương pháp giải:
Tính diện tích xung quanh hình nón, sau đó tính cung n và tạo lập theo các bước sau:
Cắt một miếng bìa hình quạt bán kính r giới hạn bởi cung 90o (một phần tư hình tròn bán kính r) và uốn miếng bìa tạo thành mặt xung quanh của hình nón.
Cắt một miếng bìa hình tròn bán kính r’ cm và dùng băng dính dán miếng bìa này với mặt xung quanh của hình nón vừa tạo.
Thể tích hình nón: \(V = \frac{1}{3}\pi {r^2}h\) (với r là bán kính đáy và h là chiều cao của hình nón).
Lời giải chi tiết:
Diện tích xung quanh của hình nón là:
\({S_{xq}} = \pi rn = \pi .5.12 = 60\pi \) cm2
Mặt xung quanh của hình nón trên là hình quạt tròn bán kính 12 cm giới hạn bởi cung no.
Ta có: \(\frac{{\pi {{.12}^2}.n}}{{360}} = 60\pi \) hay \(\frac{{2n}}{5} = 60\). Suy ra n = 150.
Từ đó, tạo lập hình nón trên theo các bước sau:
Cắt một miếng bìa hình quạt bán kính 12 cm giới hạn bởi cung 90o (một phần tư hình tròn bán kính 12 cm) và uốn miếng bìa tạo thành mặt xung quanh của hình nón.
Cắt một miếng bìa hình tròn bán kính 5 cm và dùng băng dính dán miếng bìa này với mặt xung quanh của hình nón vừa tạo.
Chiều cao của hình nón là:
\(\sqrt {{{12}^2} - {5^2}} = \sqrt {119} \) cm
Thể tích hình nón là:
\(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.5^2}\sqrt {119} \approx 285,6\) cm3.
Mục 4 của SGK Toán 9 tập 2 thường tập trung vào một chủ đề cụ thể, ví dụ như hàm số bậc nhất, hệ phương trình bậc nhất hai ẩn, hoặc các ứng dụng của phương trình bậc hai. Việc nắm vững kiến thức nền tảng và kỹ năng giải bài tập trong mục này là rất quan trọng để chuẩn bị cho các kỳ thi sắp tới.
Để giúp các em hiểu rõ hơn về nội dung bài tập, chúng ta sẽ đi vào giải chi tiết từng bài tập trong mục 4 trang 74, 75 SGK Toán 9 tập 2. Lưu ý rằng, trước khi bắt đầu giải bài tập, các em nên đọc kỹ đề bài, xác định rõ yêu cầu và các dữ kiện đã cho.
Đề bài: (Nêu rõ đề bài)
Lời giải:
Kết luận: (Nêu kết luận của bài tập)
Đề bài: (Nêu rõ đề bài)
Lời giải:
Kết luận: (Nêu kết luận của bài tập)
Trong mục 4 trang 74, 75 SGK Toán 9 tập 2, các em có thể gặp các dạng bài tập sau:
Để giải bài tập Toán 9 một cách hiệu quả, các em có thể tham khảo một số mẹo sau:
Ngoài SGK Toán 9 tập 2, các em có thể tham khảo thêm các tài liệu sau để học tập và ôn luyện:
Hy vọng rằng, với bài giải chi tiết và những lời khuyên hữu ích trên đây, các em học sinh sẽ tự tin hơn trong việc giải bài tập mục 4 trang 74, 75 SGK Toán 9 tập 2. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!
| Bài tập | Lời giải |
|---|---|
| Bài 1 | (Link đến lời giải chi tiết bài 1) |
| Bài 2 | (Link đến lời giải chi tiết bài 2) |