Chào mừng bạn đến với bài học về Lý thuyết Góc ở tâm, Cung và Hình quạt tròn trong chương trình Toán 9. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về các khái niệm này, giúp bạn giải quyết các bài toán liên quan một cách hiệu quả.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, tính chất, và các công thức liên quan đến góc ở tâm, cung và hình quạt tròn. Đồng thời, bài học cũng sẽ cung cấp các ví dụ minh họa cụ thể để bạn dễ dàng nắm bắt kiến thức.
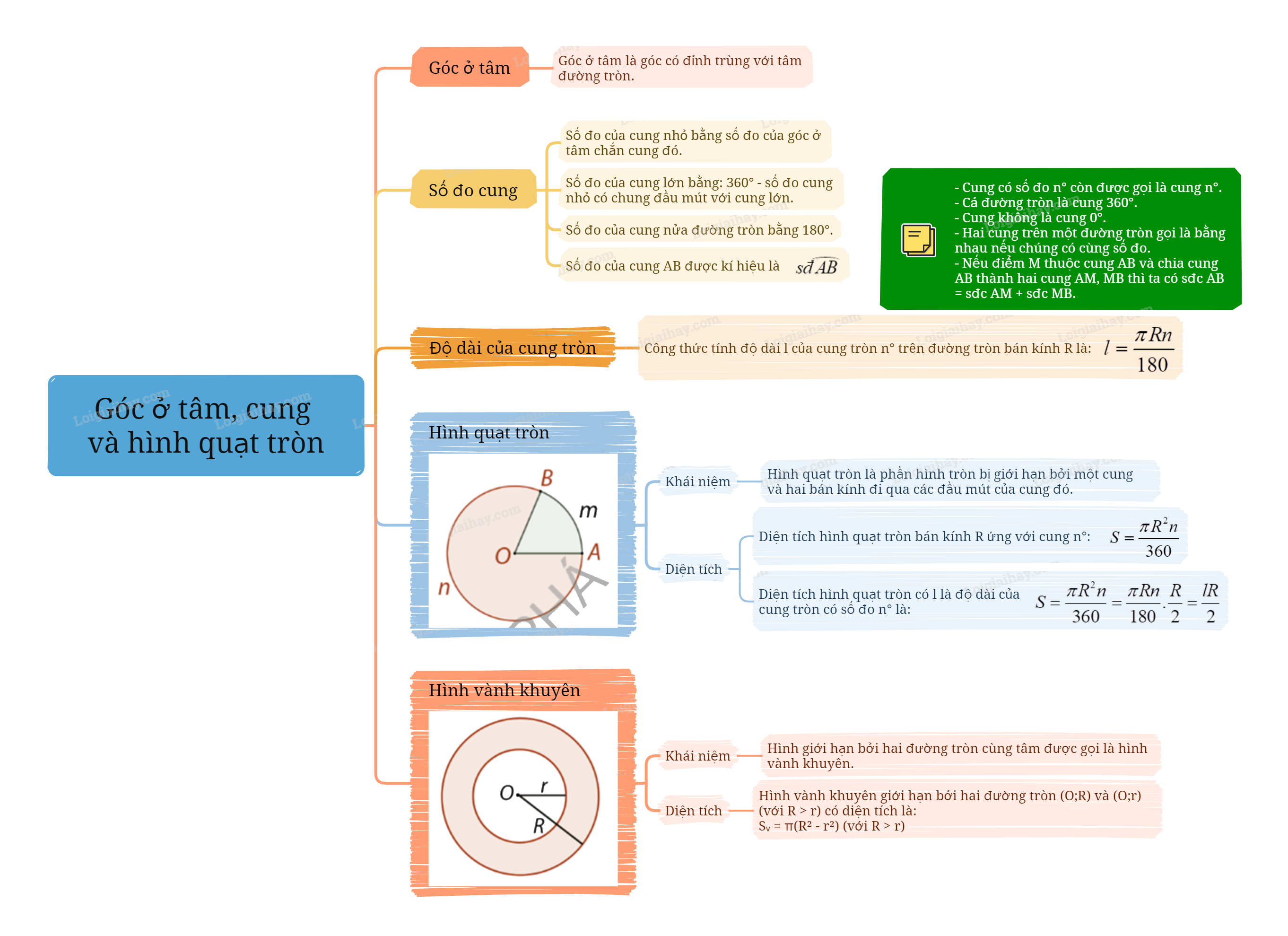
1. Góc ở tâm và số đo cung Góc ở tâm Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm của đường tròn. Số đo cung
1. Góc ở tâm và số đo cung
Góc ở tâm
Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm của đường tròn. |
Số đo cung
Trong đường tròn: - Số đo của cung nhỏ là số đo của góc ở tâm chắn cung đó; - Số đo của cung lớn là hiệu giữa \({360^0}\) và số đo của cung nhỏ cùng đầu mút với nó. - Số đo của nửa đường tròn là \({180^0}\). |
Lưu ý: Trong một đường tròn:
- Số đo của cung AB được kí hiệu là sđ$\overset\frown{AB}$.
- Các cung có số đo bằng \({n^0}\) được gọi chung là cung \({n^0}\). Mỗi điểm trên đường tròn được xem là một cung \({0^0}\), cả đường tròn được xem là cung \({360^0}\).
- Tổng số đo hai cung có chung đầu mút là \({360^0}\).
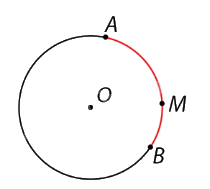
- Nếu điểm M thuộc cung AB và chia cung AB thành hai cung AM, MB thì ta có sđ$\overset\frown{AB}$ = sđ$\overset\frown{AM}$ + sđ$\overset\frown{MB}$.
2. Độ dài cung
Công thức độ dài cung \({n^0}\) của đường tròn bán kính R: \(l = \frac{{\pi Rn}}{{180}}\). |
Ví dụ:
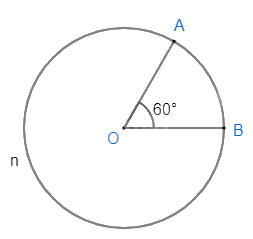
Đường tròn (O; 2cm), \(\widehat {AOB} = {60^0}\).
- Cung nhỏ AB bị chắn bởi góc ở tâm AOB.
Do đó sđ$\overset\frown{AB}=\widehat{AOB}={{60}^{0}}$.
Độ dài \({l_1}\) của cung AB là:
\({l_1} = \frac{n}{{180}}\pi R = \frac{{60}}{{180}}\pi .2 = \frac{{2\pi }}{3} \approx 2,1\left( {cm} \right)\)
Cung lớn AnB có số đo là:
sđ$\overset\frown{AmN}={{360}^{o}}-{{60}^{0}}={{300}^{0}}$.
Độ dài \({l_2}\) của cung AnB là:
\({l_2} = \frac{{300}}{{180}}\pi .2 = \frac{{10}}{3}\pi \approx 10,5\left( {cm} \right)\)
3. Diện tích hình quạt tròn và hình vành khuyên
Khái niệm hình quạt tròn
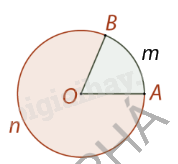
Hình quạt tròn là phần hình tròn bị giới hạn bởi một cung và hai bán kính đi qua các đầu mút của cung đó. |
Diện tích hình quạt tròn
Nếu \({S_q}\) là phần diện tích của hình quạt tròn bán kính R ứng với cung có số đo \({n^0}\) thì:
\(\frac{{{S_q}}}{{\pi {R^2}}} = \frac{n}{{360}}\).
Công thức diện tích hình quạt tròn bán kính R ứng với cung \({n^o}\): \({S_q} = \frac{{\pi {R^2}n}}{{360}}\) |
Ví dụ: Diện tích hình quạt tròn có độ dài tương ứng với nó là \(l = 4\pi \)cm, bán kính là R = 5cm là:
\({S_q} = \frac{{l.R}}{2} = \frac{{4\pi .5}}{2} = 10\pi \left( {c{m^2}} \right)\)
Khái niệm hình vành khuyên
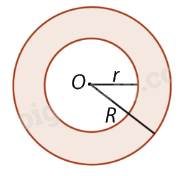
Hình vành khuyên là hình giới hạn bởi hai đường tròn đồng tâm có bán kính khác nhau. |
Diện tích hình vành khuyên
Công thức diện tích hình vành khuyên tạo bởi hai đường tròn (O;R) và (O;r) (với r < R): \({S_v} = \pi \left( {{R^2} - {r^2}} \right)\). |
Ví dụ: Diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là 3m và 5m là:
\({S_v} = \pi \left( {{5^2} - {3^2}} \right) = 16\pi \left( {{m^2}} \right)\)
Lưu ý: Từ công thức tính diện tích hình quạt tròn và độ dài cung \({n^0}\), bán kính R, ta có công thức liên hệ hai diện tích hình quạt (\({S_q}\)) với độ dài cung (\(l\)) ứng với nó như sau:
\({S_q} = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi Rn}}{{180}}.\frac{R}{2} = \frac{1}{2}lR\).
Trong chương trình Toán 9, kiến thức về góc ở tâm, cung và hình quạt tròn đóng vai trò quan trọng trong việc hiểu và giải quyết các bài toán liên quan đến đường tròn. Bài viết này sẽ cung cấp một cái nhìn tổng quan và chi tiết về các khái niệm này, cùng với các ví dụ minh họa và bài tập thực hành.
Định nghĩa: Góc ở tâm là góc có đỉnh là tâm đường tròn và hai cạnh chứa hai bán kính của đường tròn đó.
Số đo của cung: Số đo của cung là số đo của góc ở tâm chắn cung đó.
Ví dụ: Cho đường tròn (O) và cung AB. Góc AOB là góc ở tâm chắn cung AB. Số đo của cung AB bằng số đo của góc AOB.
Định nghĩa: Cung tròn là một phần của đường tròn giới hạn bởi hai điểm trên đường tròn.
Phân loại cung:
Độ dài cung: Độ dài cung được tính bằng công thức: l = πrα/180, trong đó l là độ dài cung, r là bán kính đường tròn, α là số đo góc ở tâm chắn cung đó.
Định nghĩa: Hình quạt tròn là hình được giới hạn bởi hai bán kính và một cung của đường tròn.
Diện tích hình quạt tròn: Diện tích hình quạt tròn được tính bằng công thức: S = πr2α/360, trong đó S là diện tích hình quạt tròn, r là bán kính đường tròn, α là số đo góc ở tâm chắn cung đó.
Góc ở tâm, cung và hình quạt tròn có mối quan hệ mật thiết với nhau. Góc ở tâm chắn cung, số đo của cung bằng số đo của góc ở tâm. Hình quạt tròn được tạo thành bởi hai bán kính và một cung, diện tích hình quạt tròn phụ thuộc vào bán kính và số đo góc ở tâm.
Bài 1: Cho đường tròn (O) có bán kính 5cm. Tính độ dài cung AB có số đo 72 độ.
Giải: Độ dài cung AB là: l = π * 5 * 72 / 180 = 2π (cm)
Bài 2: Cho đường tròn (O) có bán kính 8cm. Tính diện tích hình quạt tròn có số đo 135 độ.
Giải: Diện tích hình quạt tròn là: S = π * 82 * 135 / 360 = 8π (cm2)
Lý thuyết về góc ở tâm, cung và hình quạt tròn có nhiều ứng dụng trong thực tế, chẳng hạn như:
Bài viết này đã cung cấp một cái nhìn tổng quan và chi tiết về lý thuyết góc ở tâm, cung và hình quạt tròn trong chương trình Toán 9. Hy vọng rằng, với những kiến thức này, bạn sẽ có thể giải quyết các bài toán liên quan một cách tự tin và hiệu quả.
Việc nắm vững lý thuyết và thực hành giải nhiều bài tập khác nhau là chìa khóa để thành công trong môn Toán. Chúc bạn học tập tốt!