Chào mừng bạn đến với bài học về Lý thuyết Hình trụ Toán 9 tại giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về hình trụ, giúp bạn hiểu rõ cấu trúc, tính chất và các công thức liên quan.
Chúng tôi tin rằng, với phương pháp tiếp cận dễ hiểu, bài giảng chi tiết và bài tập thực hành phong phú, bạn sẽ dễ dàng nắm bắt kiến thức và tự tin áp dụng vào giải các bài tập toán 9.
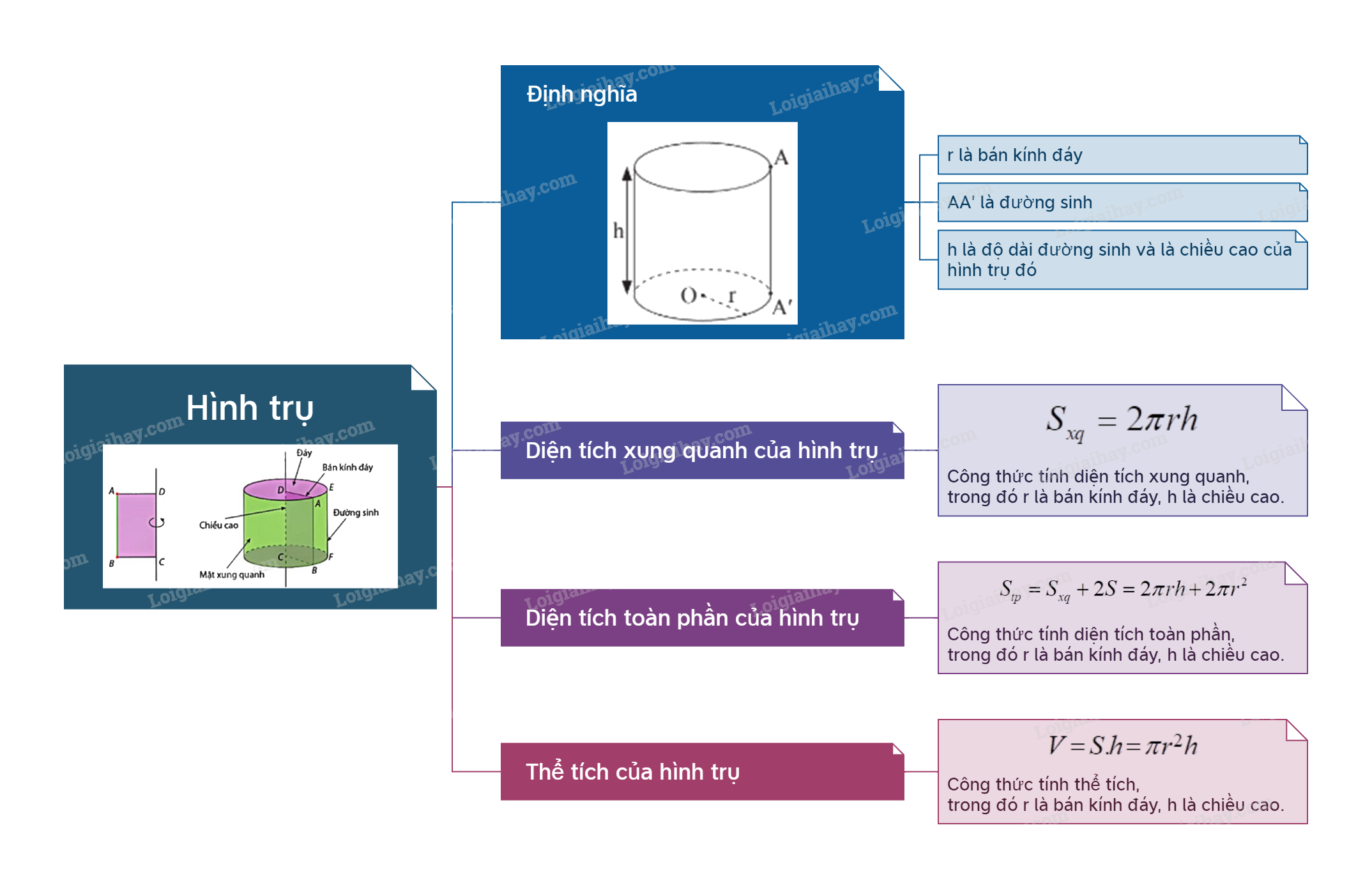
Định nghĩa Ví dụ: Hình trụ trên có: + r là bán kính đáy; + AA’ là đường sinh; + h là độ dài đường sinh và là chiều cao của hình trụ đó.
Định nghĩa
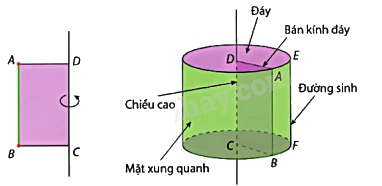
Ví dụ:
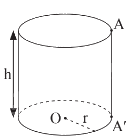
Hình trụ trên có:
+ r là bán kính đáy;
+ AA’ là đường sinh;
+ h là độ dài đường sinh và là chiều cao của hình trụ đó.
2. Diện tích xung quanh của hình trụ
Diện tích xung quanh của hình trụ
Diện tích xung quanh \({S_{xq}}\) của hình trụ có bán kính đáy r và chiều cao h là: \({S_{xq}} = 2\pi rh\). |
Diện tích toàn phần của hình trụ
Diện tích toàn phần \({S_{tp}}\) của hình trụ có bán kính đáy r và chiều cao h là: \({S_{tp}} = {S_{xq}} + 2S = 2\pi rh + 2\pi {r^2}\) (S là diện tích đáy của hình trụ). |
Ví dụ:
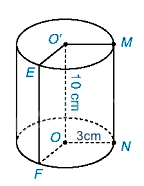
Diện tích xung quanh của hình trụ là:
\({S_{xq}} = 2\pi rh = 2\pi .3.10 = 60\pi \left( {c{m^2}} \right)\)
3. Thể tích của hình trụ
Thể tích V của hình trụ có bán kính đáy r và chiều cao h là: \(V = S.h = \pi {r^2}h\) (S là diện tích đáy của hình trụ).
|
Ví dụ:
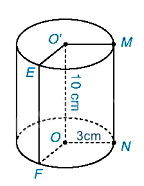
Diện tích đáy là:
\(S = \pi {r^2} = \pi {.3^2} = 9\pi \left( {c{m^2}} \right)\)
Thể tích của hình trụ là:
\(V = S.h = 9\pi .10 = 90\pi \left( {c{m^3}} \right)\)
Hình trụ là một trong những hình học quan trọng trong chương trình Toán 9. Hiểu rõ lý thuyết về hình trụ là nền tảng để giải quyết các bài toán liên quan đến diện tích bề mặt và thể tích của hình trụ. Bài viết này sẽ cung cấp một cái nhìn tổng quan và chi tiết về lý thuyết hình trụ, bao gồm định nghĩa, các yếu tố của hình trụ, công thức tính diện tích và thể tích, cùng với các ví dụ minh họa.
Hình trụ là một hình khối được tạo thành bởi hai hình tròn bằng nhau, song song với nhau và một mặt bên là mặt xung quanh của hình trụ. Hai hình tròn này được gọi là hai đáy của hình trụ. Khoảng cách giữa hai đáy gọi là chiều cao của hình trụ.
Diện tích bề mặt của hình trụ bao gồm diện tích hai đáy và diện tích mặt xung quanh.
Thể tích của hình trụ được tính bằng diện tích đáy nhân với chiều cao.
Các bài toán về hình trụ thường yêu cầu tính diện tích bề mặt, thể tích hoặc tìm các yếu tố của hình trụ khi biết một số thông tin khác. Dưới đây là một số dạng bài tập thường gặp:
Ví dụ 1: Một hình trụ có bán kính đáy r = 5cm và chiều cao h = 10cm. Tính diện tích toàn phần và thể tích của hình trụ.
Giải:
Ví dụ 2: Một hình trụ có thể tích V = 300π cm3 và chiều cao h = 12cm. Tính bán kính đáy của hình trụ.
Giải:
V = πr2h => r2 = V / (πh) = 300π / (π * 12) = 25 => r = 5cm
Để nắm vững lý thuyết về hình trụ, bạn nên luyện tập thêm nhiều bài tập khác nhau. Bạn có thể tìm thấy các bài tập về hình trụ trong sách giáo khoa, sách bài tập hoặc trên các trang web học toán online như giaitoan.edu.vn.
Lý thuyết Hình trụ Toán 9 là một phần quan trọng trong chương trình học. Việc hiểu rõ các định nghĩa, công thức và các bài toán thường gặp sẽ giúp bạn tự tin giải quyết các bài tập và đạt kết quả tốt trong môn Toán. Chúc bạn học tập tốt!