Chào mừng các em học sinh đến với bài giải bài tập 4.12 trang 87 SGK Toán 9 tập 1 trên giaitoan.edu.vn. Bài tập này thuộc chương Hàm số bậc nhất và là một phần quan trọng trong việc củng cố kiến thức về hàm số.
Chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững phương pháp giải và tự tin làm bài tập.
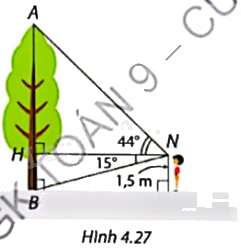
Quan sát Hình 4.27 và tính: a) Khoảng cách NH giữa Nam và cây; b) Chiều cao AB của cây.
Đề bài
Quan sát Hình 4.27 và tính:
a) Khoảng cách NH giữa Nam và cây;
b) Chiều cao AB của cây.
Phương pháp giải - Xem chi tiết
a) Ta có: \(HB = 1,5m\)
Tam giác NHB vuông tại H nên \(NH = NB.\cot HNB\)
b) Tam giác AHN vuông tại H nên \(AH = NH.\tan HNA\).
Do đó, \(AB = HB + HA\)
Lời giải chi tiết
a) Ta có: \(HB = 1,5m\).
Tam giác NHB vuông tại H nên
\(NH = NB.\cot HNB = 1,5.\cot {15^o} \approx 5,6\left( m \right)\).
b) Tam giác AHN vuông tại H nên
\(AH = NH.\tan HNA \approx 5,6.\tan {44^o} \approx 5,4\left( m \right)\).
Do đó, \(AB = HB + HA \approx 1,5 + 5,4 \approx 6,9\left( m \right)\).
Bài tập 4.12 trang 87 SGK Toán 9 tập 1 yêu cầu chúng ta xét hàm số y = (m-2)x + 3. Để hàm số này là hàm số bậc nhất, điều kiện cần và đủ là hệ số của x khác 0, tức là m-2 ≠ 0. Bài viết này sẽ đi sâu vào phân tích điều kiện này và cách xác định giá trị của m để đảm bảo hàm số thỏa mãn yêu cầu.
Hàm số y = ax + b được gọi là hàm số bậc nhất khi và chỉ khi a ≠ 0. Trong trường hợp bài tập này, a = m-2. Do đó, để y = (m-2)x + 3 là hàm số bậc nhất, chúng ta cần có:
m - 2 ≠ 0
Giải phương trình này, ta được:
m ≠ 2
Điều kiện m ≠ 2 có nghĩa là giá trị của m không thể bằng 2. Nếu m = 2, hàm số sẽ trở thành y = (2-2)x + 3 = 0x + 3 = 3, đây là một hàm số hằng, không phải hàm số bậc nhất. Do đó, để đảm bảo hàm số là hàm số bậc nhất, m phải khác 2.
Xét các trường hợp sau:
Hàm số trở thành y = (1-2)x + 3 = -x + 3. Đây là hàm số bậc nhất vì hệ số của x là -1 ≠ 0.
Hàm số trở thành y = (3-2)x + 3 = x + 3. Đây là hàm số bậc nhất vì hệ số của x là 1 ≠ 0.
Hàm số trở thành y = (2-2)x + 3 = 3. Đây là hàm số hằng, không phải hàm số bậc nhất.
Hàm số bậc nhất có dạng y = ax + b, trong đó a và b là các số thực. Hàm số bậc nhất có các tính chất quan trọng sau:
Để củng cố kiến thức về hàm số bậc nhất, các em có thể làm thêm các bài tập sau:
Bài tập 4.12 trang 87 SGK Toán 9 tập 1 là một bài tập cơ bản giúp các em hiểu rõ hơn về điều kiện để một hàm số là hàm số bậc nhất. Việc nắm vững kiến thức này sẽ giúp các em giải quyết các bài tập phức tạp hơn về hàm số bậc nhất trong tương lai.
Hy vọng bài giải chi tiết này sẽ giúp các em học tốt môn Toán 9. Chúc các em học tập tốt!