Chào mừng các em học sinh đến với bài giải chi tiết mục 2 trang 63, 64 SGK Toán 9 tập 2 trên giaitoan.edu.vn. Bài viết này sẽ cung cấp cho các em những phương pháp giải bài tập hiệu quả, giúp các em hiểu rõ hơn về kiến thức đã học.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp các em học Toán dễ dàng và thú vị hơn.
Một hộp hình trụ làm bằng thiếc có bán kính 5 cm, chiều cao 8 cm (Hình 9.4a). Nếu cắt rời hai đáy và cắt dọc theo đường sinh AB của hộp, rồi trải phẳng ra, ta được hình khai triển của hình trụ (Hình 9.4b). a) Tính chu vi mỗi đáy của hình trụ. b) Tính diện tích miếng thiếc hình chữ nhật để làm thành mặt xung quanh của hộp (diện tích các mối nối không đáng kể).
Trả lời câu hỏi Vận dụng 1 trang 64SGK Toán 9 Cùng khám phá
Diện tích giấy tối thiểu để quấn quanh một hộp đào ngâm có dạng hình trụ (Hình 9.6) là bao nhiêu centimet vuông (làm tròn kết quả đến hàng phần trăm), biết rằng người ta chỉ quấn một lớp giấy quanh hộp đào?
Phương pháp giải:
Diện tích xung quanh hình trụ là \({S_{xq}} = 2\pi rh\) (với r là bán kính đáy và h là chiều cao hình trụ).
Lời giải chi tiết:
Diện tích xung quanh hình trụ là:
\({S_{xq}} = 2\pi rh = 2\pi .50.120 = 12000\pi \approx 37699,11\left( {m{m^2}} \right)\)
Vậy diện tích giấy tối thiểu để quấn quanh một hộp đào là 37699,11 mm2.
Trả lời câu hỏi Luyện tập 2 trang 64 SGK Toán 9 Cùng khám phá
Tính diện tích xung quanh của hình trụ có hình khai triển như Hình 9.5.
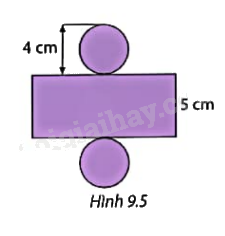
Phương pháp giải:
Diện tích xung quanh hình trụ là \({S_{xq}} = 2\pi rh\).
Lời giải chi tiết:
Diện tích xung quanh hình trụ là:
\({S_{xq}} = 2\pi rh = 2\pi .2.5 = 20\pi \)\(c{m^2}\).
Trả lời câu hỏi Hoạt động 2 trang 63SGK Toán 9 Cùng khám phá
Một hộp hình trụ làm bằng thiếc có bán kính 5 cm, chiều cao 8 cm (Hình 9.4a). Nếu cắt rời hai đáy và cắt dọc theo đường sinh AB của hộp, rồi trải phẳng ra, ta được hình khai triển của hình trụ (Hình 9.4b).
a) Tính chu vi mỗi đáy của hình trụ.
b) Tính diện tích miếng thiếc hình chữ nhật để làm thành mặt xung quanh của hộp (diện tích các mối nối không đáng kể).
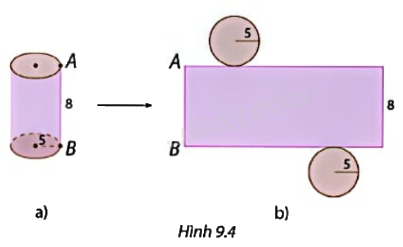
Phương pháp giải:
Chu vi đường tròn: \(2\pi r\).
Diện tích hình chữ nhật bằng: a.b (a,b lần lượt là chiều dài và chiều rộng).
Lời giải chi tiết:
a) Chu vi mỗi đáy của hình trụ là:
\(2\pi r = 2.5\pi = 10\pi \) cm.
b) Diện tích hình chữ nhật là:
8.10\(\pi \)= 80\(\pi \).
Trả lời câu hỏi Hoạt động 2 trang 63SGK Toán 9 Cùng khám phá
Một hộp hình trụ làm bằng thiếc có bán kính 5 cm, chiều cao 8 cm (Hình 9.4a). Nếu cắt rời hai đáy và cắt dọc theo đường sinh AB của hộp, rồi trải phẳng ra, ta được hình khai triển của hình trụ (Hình 9.4b).
a) Tính chu vi mỗi đáy của hình trụ.
b) Tính diện tích miếng thiếc hình chữ nhật để làm thành mặt xung quanh của hộp (diện tích các mối nối không đáng kể).
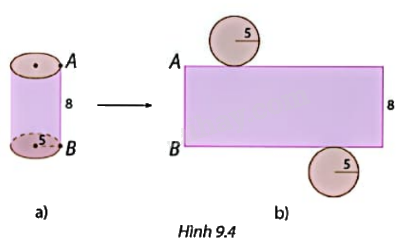
Phương pháp giải:
Chu vi đường tròn: \(2\pi r\).
Diện tích hình chữ nhật bằng: a.b (a,b lần lượt là chiều dài và chiều rộng).
Lời giải chi tiết:
a) Chu vi mỗi đáy của hình trụ là:
\(2\pi r = 2.5\pi = 10\pi \) cm.
b) Diện tích hình chữ nhật là:
8.10\(\pi \)= 80\(\pi \).
Trả lời câu hỏi Luyện tập 2 trang 64 SGK Toán 9 Cùng khám phá
Tính diện tích xung quanh của hình trụ có hình khai triển như Hình 9.5.
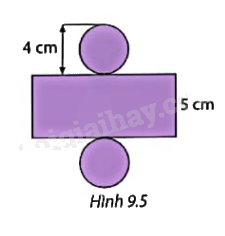
Phương pháp giải:
Diện tích xung quanh hình trụ là \({S_{xq}} = 2\pi rh\).
Lời giải chi tiết:
Diện tích xung quanh hình trụ là:
\({S_{xq}} = 2\pi rh = 2\pi .2.5 = 20\pi \)\(c{m^2}\).
Trả lời câu hỏi Vận dụng 1 trang 64SGK Toán 9 Cùng khám phá
Diện tích giấy tối thiểu để quấn quanh một hộp đào ngâm có dạng hình trụ (Hình 9.6) là bao nhiêu centimet vuông (làm tròn kết quả đến hàng phần trăm), biết rằng người ta chỉ quấn một lớp giấy quanh hộp đào?
Phương pháp giải:
Diện tích xung quanh hình trụ là \({S_{xq}} = 2\pi rh\) (với r là bán kính đáy và h là chiều cao hình trụ).
Lời giải chi tiết:
Diện tích xung quanh hình trụ là:
\({S_{xq}} = 2\pi rh = 2\pi .50.120 = 12000\pi \approx 37699,11\left( {m{m^2}} \right)\)
Vậy diện tích giấy tối thiểu để quấn quanh một hộp đào là 37699,11 mm2.
Mục 2 của SGK Toán 9 tập 2 thường tập trung vào một chủ đề cụ thể trong hình học hoặc đại số. Để giải quyết các bài tập trong mục này, học sinh cần nắm vững các định nghĩa, tính chất và định lý liên quan. Bài viết này sẽ đi sâu vào từng bài tập trong trang 63 và 64, cung cấp lời giải chi tiết và dễ hiểu.
Bài tập 1 thường là bài tập áp dụng trực tiếp các kiến thức đã học. Để giải bài tập này, học sinh cần:
Ví dụ, nếu bài tập yêu cầu tính độ dài một đoạn thẳng, học sinh cần sử dụng công thức tính độ dài đoạn thẳng và thay các giá trị đã cho vào công thức.
Bài tập 2 có thể là bài tập chứng minh hoặc bài tập tìm kiếm. Để giải bài tập này, học sinh cần:
Ví dụ, nếu bài tập yêu cầu chứng minh hai tam giác bằng nhau, học sinh cần sử dụng các trường hợp bằng nhau của tam giác và chứng minh các cạnh tương ứng bằng nhau.
Bài tập 3 có thể là bài tập vận dụng kiến thức vào thực tế. Để giải bài tập này, học sinh cần:
Ví dụ, nếu bài tập yêu cầu tính diện tích một mảnh đất hình chữ nhật, học sinh cần sử dụng công thức tính diện tích hình chữ nhật và thay các giá trị đã cho vào công thức.
Bài tập 4 có thể là bài tập tổng hợp các kiến thức đã học. Để giải bài tập này, học sinh cần:
Ví dụ, bài tập có thể yêu cầu giải một hệ phương trình hoặc chứng minh một bất đẳng thức.
Để giải bài tập Toán 9 tập 2 một cách hiệu quả, học sinh cần:
Hy vọng rằng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong mục 2 trang 63, 64 SGK Toán 9 tập 2. Chúc các em học tập tốt và đạt kết quả cao!