Chào mừng bạn đến với bài học về Lý thuyết Tứ giác nội tiếp Toán 9 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp cho bạn một cách toàn diện kiến thức về tứ giác nội tiếp, từ định nghĩa, các tính chất quan trọng đến các ứng dụng thực tế trong giải toán.
Chúng ta sẽ cùng nhau khám phá những điều thú vị và hữu ích về loại tứ giác đặc biệt này, giúp bạn tự tin hơn trong các bài kiểm tra và kỳ thi.
1. Khái niệm tứ giác nội tiếp - Một tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn. - Đường tròn đi qua bốn đỉnh của tứ giác gọi là đường tròn ngoại tiếp tứ giác đó.
1. Khái niệm tứ giác nội tiếp
- Một tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn. - Đường tròn đi qua bốn đỉnh của tứ giác gọi là đường tròn ngoại tiếp tứ giác đó. |
Ví dụ:
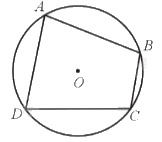
Tứ giác ABCD là tứ giác nội tiếp và đường tròn (O) được gọi là đường tròn ngoại tiếp tứ giác ABCD.
Hình chữ nhật, hình vuông là các tứ giác nội tiếp. Đường tròn ngoại tiếp của hình chữ nhật và hình vuông có tâm là giao điểm của hai đường chéo và bán kính là nửa đường chéo.
|
Ví dụ:
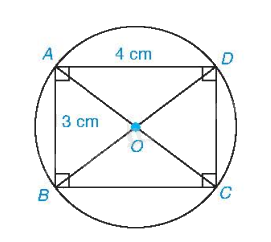
Áp dụng định lí Pythagore cho tam giác ABD vuông tại A, ta có:
\(B{D^2} = A{B^2} + A{D^2} = {3^2} + {4^2} = 25\) nên \(BD = 5cm\).
Do đó, ta có \(R = \frac{{BD}}{2} = 2,5cm\).
Đường tròn (O;2,5) là đường tròn ngoại tiếp hình chữ nhật ABCD.
2. Tính chất
Trong một tứ giác nội tiếp đường tròn, tổng số đo hai góc đối bằng \(180^\circ \). |
Ví dụ:
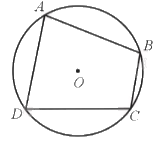
Tứ giác ABCD nội tiếp (O) nên \(\widehat A + \widehat C = 180^\circ ;\widehat B + \widehat D = 180^\circ \).
Trong chương trình Toán 9, kiến thức về tứ giác nói chung và tứ giác nội tiếp nói riêng đóng vai trò quan trọng. Việc nắm vững lý thuyết và kỹ năng giải bài tập liên quan sẽ giúp học sinh đạt kết quả tốt trong các bài kiểm tra và kỳ thi. Bài viết này sẽ trình bày chi tiết về lý thuyết tứ giác nội tiếp, bao gồm định nghĩa, các tính chất, dấu hiệu nhận biết và ứng dụng của nó.
Một tứ giác được gọi là tứ giác nội tiếp đường tròn nếu bốn đỉnh của nó cùng nằm trên một đường tròn. Nói cách khác, tồn tại một đường tròn đi qua cả bốn đỉnh của tứ giác đó.
Tứ giác nội tiếp có những tính chất quan trọng sau:
Có một số dấu hiệu để nhận biết một tứ giác là tứ giác nội tiếp:
Lý thuyết tứ giác nội tiếp được ứng dụng rộng rãi trong giải các bài toán hình học, đặc biệt là các bài toán liên quan đến đường tròn. Một số ứng dụng phổ biến bao gồm:
Bài tập 1: Cho tứ giác ABCD nội tiếp đường tròn. Biết ∠A = 80° và ∠C = 100°. Tính số đo của ∠B và ∠D.
Giải: Vì ABCD là tứ giác nội tiếp nên ∠A + ∠C = 180° và ∠B + ∠D = 180°. Tuy nhiên, đề bài cho ∠A = 80° và ∠C = 100° nên ∠A + ∠C = 180°. Do đó, ∠B + ∠D = 180°. Không thể xác định chính xác ∠B và ∠D chỉ với thông tin này.
Bài tập 2: Cho tam giác ABC vuông tại A. Gọi O là trung điểm của cạnh huyền BC. Trên đường tròn (O, R) lấy điểm D sao cho BD = CD. Chứng minh tứ giác ABDC là tứ giác nội tiếp.
Giải: Vì O là trung điểm của BC và BD = CD nên OD là đường trung tuyến của tam giác BCD ứng với cạnh BC. Do đó, OD = BD = CD. Suy ra, tam giác BOD và tam giác COD là các tam giác cân tại D. Từ đó, ta có ∠DBO = ∠DBO và ∠DCO = ∠DCO. Vì ∠BAC = 90° nên ∠BOC = 2∠BAC = 180°. Do đó, BC là đường kính của đường tròn (O, R). Vì D nằm trên đường tròn (O, R) và BC là đường kính nên ∠BDC = 90°. Vậy, tứ giác ABDC có ∠BAC = 90° và ∠BDC = 90° nên ABDC là tứ giác nội tiếp.
Lý thuyết Tứ giác nội tiếp Toán 9 là một phần kiến thức quan trọng và có nhiều ứng dụng trong giải toán. Việc nắm vững định nghĩa, tính chất, dấu hiệu nhận biết và các ứng dụng của tứ giác nội tiếp sẽ giúp học sinh tự tin hơn trong việc giải các bài toán hình học. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích và đầy đủ về chủ đề này.