Chào mừng bạn đến với chuyên mục Lý thuyết Đường tròn Toán 9 tại giaitoan.edu.vn! Đây là một trong những chủ đề quan trọng bậc nhất trong chương trình Hình học lớp 9, đóng vai trò then chốt trong việc xây dựng nền tảng kiến thức vững chắc cho các bài học tiếp theo.
Chúng tôi cung cấp một hệ thống lý thuyết đầy đủ, dễ hiểu, kết hợp với các ví dụ minh họa sinh động và bài tập thực hành đa dạng, giúp bạn nắm vững kiến thức một cách nhanh chóng và hiệu quả.
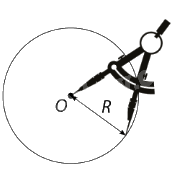
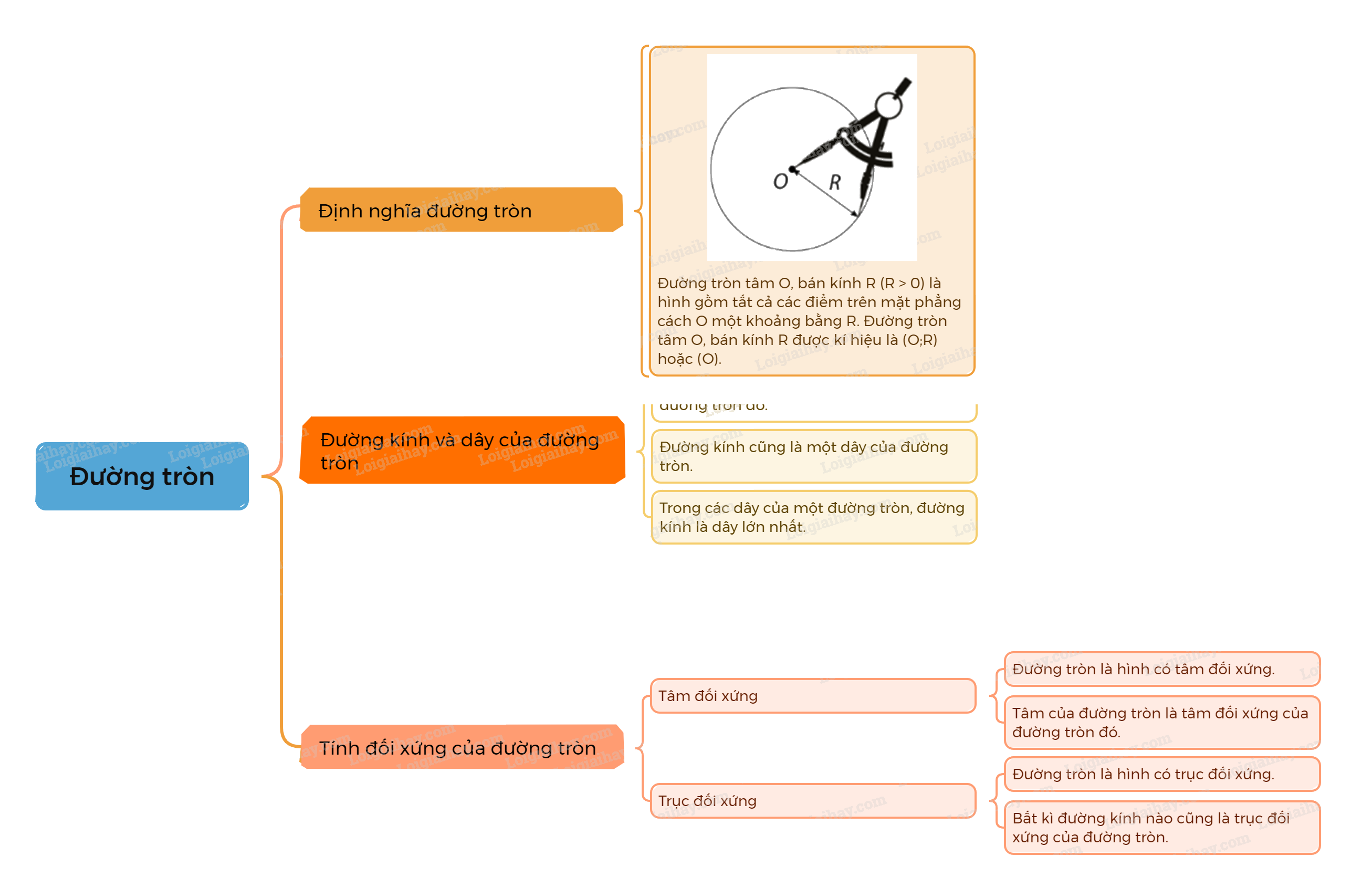
1. Tính đối xứng và trục đối xứng của đường tròn Định nghĩa đường tròn Đường tròn tâm O, bán kính R (R > 0) là hình gồm tất cả các điểm trên mặt phẳng cách O một khoảng bằng R. Đường tròn tâm O, bán kính R được kí hiệu là (O;R) hoặc (O).
1. Tính đối xứng và trục đối xứng của đường tròn
Định nghĩa đường tròn
Đường tròn tâm O, bán kính R (R > 0) là hình gồm tất cả các điểm trên mặt phẳng cách O một khoảng bằng R. Đường tròn tâm O, bán kính R được kí hiệu là (O;R) hoặc (O). |
Tâm đối xứng của đường tròn
Đường tròn là hình có tâm đối xứng. Tâm của đường tròn là tâm đối xứng của đường tròn đó. |
Trục đối xứng của đường tròn
Đường tròn là hình có trục đối xứng. Bất kì đường kính nào cũng là trục đối xứng của đường tròn. |
2. Đường kính và dây của đường tròn
Đoạn thẳng nối hai điểm phân biệt của đường tròn được gọi là một dây của đường tròn đó.
Lưu ý:Đường kính cũng là một dây của đường tròn.
Ví dụ:
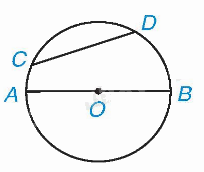
Trong hình trên, CD là một dây, AB là một đường kính của (O).
Mối liên hệ giữa độ dài đường kính và độ dài dây của một đường tròn
Trong các dây của một đường tròn, đường kính là dây lớn nhất. |
Đường tròn là một trong những hình học cơ bản và quan trọng trong toán học. Trong chương trình Toán 9, việc nắm vững lý thuyết đường tròn là điều kiện cần thiết để giải quyết các bài toán liên quan đến hình học, đặc biệt là các bài toán chứng minh và tính toán.
Đường tròn là tập hợp tất cả các điểm nằm trên một mặt phẳng, cách một điểm cố định (gọi là tâm) một khoảng không đổi (gọi là bán kính).
Có ba trường hợp vị trí tương đối giữa đường thẳng và đường tròn:
Tiếp tuyến của đường tròn là đường thẳng chỉ có một điểm chung với đường tròn. Điểm chung đó gọi là tiếp điểm.
Tính chất: Tiếp tuyến tại một điểm của đường tròn vuông góc với bán kính tại điểm đó.
Góc ở tâm: Góc có đỉnh là tâm đường tròn.
Góc nội tiếp: Góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai điểm trên đường tròn.
Mối quan hệ: Góc nội tiếp bằng nửa góc ở tâm cùng chắn một cung.
Bài tập 1: Cho đường tròn (O) có bán kính R = 5cm. Vẽ dây AB có độ dài 6cm. Tính khoảng cách từ tâm O đến dây AB.
Giải: Gọi H là trung điểm của AB. Khi đó, OH vuông góc với AB. Áp dụng định lý Pitago vào tam giác OHA, ta có:
OH2 + HA2 = OA2
OH2 + 32 = 52
OH2 = 16
OH = 4cm
Bài tập 2: Cho đường tròn (O) và một điểm A nằm ngoài đường tròn. Vẽ tiếp tuyến AB và AC đến đường tròn. Chứng minh rằng OA là đường phân giác của góc BAC.
Lý thuyết đường tròn có ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và thực tế, như:
Để nắm vững lý thuyết đường tròn, bạn nên luyện tập thường xuyên các bài tập khác nhau. Hãy tìm kiếm các bài tập trên giaitoan.edu.vn hoặc trong sách giáo khoa để rèn luyện kỹ năng giải toán của mình.
Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!