Giải bài tập 6.3 trang 5 SGK Toán 9 tập 2

Giải bài tập 6.3 trang 5 SGK Toán 9 tập 2 - Cùng khám phá

Giải bài tập 6.3 trang 5 SGK Toán 9 tập 2

Chào mừng các em học sinh đến với bài giải bài tập 6.3 trang 5 SGK Toán 9 tập 2 của giaitoan.edu.vn. Bài tập này thuộc chương Hàm số bậc nhất và ứng dụng, một trong những chương quan trọng của môn Toán lớp 9.

Chúng tôi sẽ cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán. Hãy cùng bắt đầu nhé!

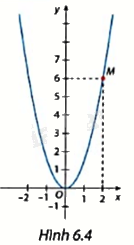
Cho hàm số y = ax2 có đồ thị là đường parabol như Hình 6.4 a) Tìm hệ số a. b) Tìm tung độ của điểm thuộc đồ thị có hoành độ bằng -1. c) Tìm các điểm thuộc đồ thị có tung độ bằng \(\frac{2}{3}\).

Đề bài

Cho hàm số y = ax² có đồ thị là đường parabol như Hình 6.4

a) Tìm hệ số a.

b) Tìm tung độ của điểm thuộc đồ thị có hoành độ bằng -1.

c) Tìm các điểm thuộc đồ thị có tung độ bằng \(\frac{2}{3}\).

Giải bài tập 6.3 trang 5 SGK Toán 9 tập 2 - Cùng khám phá 1

Phương pháp giải - Xem chi tiết Giải bài tập 6.3 trang 5 SGK Toán 9 tập 2 - Cùng khám phá 2

Thay toạ độ điểm M(2;6) vào y = ax² để tìm a.

Thay x = -1 để tìm y.

Thay y = \(\frac{2}{3}\) để tìm x.

Lời giải chi tiết

a) Thay toạ độ điểm M(2;6) vào y = ax² ta có:

6 = a.2²

a = \(\frac{3}{2}\)

b) Thay x = -1 vào y = \(\frac{3}{2}\)x² ta được y = \( - \frac{3}{2}{( - 1)^2} = - \frac{3}{2}\).

Điểm cần tìm là \(\left( { - 1; - \frac{3}{2}} \right)\).

c) Thay y = \(\frac{2}{3}\) vào y = \(\frac{3}{2}\)x² ta được

\(\begin{array}{l}\frac{2}{3} = \frac{3}{2}{x^2}\\{x^2} = \frac{4}{9}\\\left[ {\begin{array}{*{20}{c}}{x = \frac{2}{3}}\\{x = - \frac{2}{3}}\end{array}} \right.\end{array}\)

Điểm cần tìm là \(\left( {\frac{2}{3};\frac{2}{3}} \right);\left( { - \frac{2}{3};\frac{2}{3}} \right)\).

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài tập 6.3 trang 5 SGK Toán 9 tập 2 - Cùng khám phá đặc sắc thuộc chuyên mục giải bài tập toán lớp 9 trên nền tảng soạn toán. Với bộ bài tập toán thcs được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài tập 6.3 trang 5 SGK Toán 9 tập 2: Tìm hệ số góc và vẽ đồ thị

Bài tập 6.3 trang 5 SGK Toán 9 tập 2 yêu cầu chúng ta tìm hệ số góc của đường thẳng và vẽ đồ thị của hàm số bậc nhất. Để giải bài tập này, chúng ta cần nắm vững các kiến thức cơ bản về hàm số bậc nhất, bao gồm:

Hàm số bậc nhất là gì? Hàm số bậc nhất có dạng y = ax + b, trong đó a và b là các số thực, a ≠ 0.
Hệ số góc của đường thẳng là gì? Hệ số góc của đường thẳng y = ax + b là số a. Hệ số góc cho biết độ dốc của đường thẳng.
Cách vẽ đồ thị của hàm số bậc nhất? Để vẽ đồ thị của hàm số bậc nhất, ta cần xác định hai điểm thuộc đồ thị, sau đó nối hai điểm đó lại với nhau.

Lời giải chi tiết bài tập 6.3 trang 5 SGK Toán 9 tập 2

Bài 6.3: Tìm hệ số góc của các đường thẳng sau đây:

a) y = 5x - 3
b) y = -2x + 1
c) y = x + 7
d) y = -x - 5

Giải:

a) Đường thẳng y = 5x - 3 có hệ số góc là 5.
b) Đường thẳng y = -2x + 1 có hệ số góc là -2.
c) Đường thẳng y = x + 7 có hệ số góc là 1.
d) Đường thẳng y = -x - 5 có hệ số góc là -1.

Vẽ đồ thị hàm số bậc nhất

Để vẽ đồ thị của hàm số bậc nhất, ta thực hiện các bước sau:

Xác định hai điểm thuộc đồ thị. Thông thường, ta chọn x = 0 và x = 1 để tìm ra hai điểm tương ứng.
Vẽ hệ trục tọa độ Oxy.
Đánh dấu hai điểm đã xác định trên hệ trục tọa độ.
Nối hai điểm đó lại với nhau bằng một đường thẳng. Đường thẳng này chính là đồ thị của hàm số bậc nhất.

Ví dụ minh họa

Vẽ đồ thị của hàm số y = 2x + 1.

Giải:

Khi x = 0, ta có y = 2(0) + 1 = 1. Vậy điểm A(0; 1) thuộc đồ thị.
Khi x = 1, ta có y = 2(1) + 1 = 3. Vậy điểm B(1; 3) thuộc đồ thị.
Vẽ hệ trục tọa độ Oxy.
Đánh dấu hai điểm A(0; 1) và B(1; 3) trên hệ trục tọa độ.
Nối hai điểm A và B lại với nhau bằng một đường thẳng. Đường thẳng AB chính là đồ thị của hàm số y = 2x + 1.

Luyện tập thêm

Để củng cố kiến thức về hàm số bậc nhất và cách vẽ đồ thị, các em có thể tự giải thêm các bài tập sau:

Bài 6.4 trang 5 SGK Toán 9 tập 2
Bài 6.5 trang 5 SGK Toán 9 tập 2

Kết luận

Bài tập 6.3 trang 5 SGK Toán 9 tập 2 là một bài tập cơ bản về hàm số bậc nhất. Việc nắm vững kiến thức và kỹ năng giải bài tập này sẽ giúp các em học tốt môn Toán lớp 9. Chúc các em học tập tốt!