Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 2 trang 136, 137, 138 của sách giáo khoa Toán 11 tập 1.
Mục tiêu của chúng tôi là cung cấp cho các em những lời giải chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Xét mẫu số liệu ghép nhóm cho bới Bảng 5.16 trong Hoạt động 1.
Xét mẫu số liệu ghép nhóm cho bới Bảng 5.16 trong Hoạt động 1.
a, Lập bảng tần số tích lũy của mẫu số liệu đã cho
b, Gọi \({M_e}\) là trung vị của mẫu số liệu. Tìm nhóm chứa trung vị \({M_e}\). Gọi h là độ dài nhóm đó. Tìm h.
c, Xác định số số liệu:
Nhỏ hơn 158
Thuộc nhóm [158,161)
Nhỏ hơn hoặc bằng \({M_e}\)
Thuộc đoạn [158, \({M_e}\)].
Phương pháp giải:
a, Lập bảng tần số tích lũy
b, Dựa vào câu a tìm nhóm chứa trung vị. độ dài nhóm bằng số hạng cuối trừ số hạng đầu của nhóm đó.
c, Dựa vào câu a xác định các yêu cầu.
Lời giải chi tiết:
a,
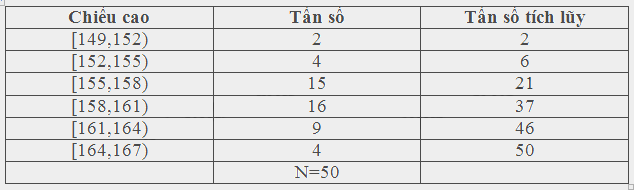
b, Ta có : \(\frac{N}{2} = \frac{{50}}{2} = 25\).Nhóm chứa trung vị \({M_e}\) là [158,161)
Độ dài nhóm này là: h= 161 - 158 = 3
c, Số số liệu nhỏ hơn 158 là: 21
Số số liệu thuộc nhóm [158,161) là 16
Số số liệu nhỏ hơn hoặc bằng \({M_e}\) là 25
Số số liệu thuộc đoạn [158, \({M_e}\)] là 4
Xác định trung vị của mẫu số liệu ghép nhóm cho trong Luyện tập 1
Phương pháp giải:
Dùng công thức tính \({M_e} = {L_m} + \frac{{\frac{N}{2} - T}}{{{n_m}}}.h\)
Lời giải chi tiết:
Ta có: \({L_m} = 6\), \(\frac{N}{2} = \frac{{160}}{2} = 80\), T= 63, \({n_m} = 30\), h= 2
\({M_e} = {L_m} + \frac{{\frac{N}{2} - T}}{{{n_m}}}.h = 6 + \frac{{80 - 63}}{{30}}.2 \approx 7,13\)
Mục 2 của SGK Toán 11 tập 1 tập trung vào phương pháp tọa độ trong không gian, một phần kiến thức nền tảng quan trọng cho các chương trình học toán ở các lớp trên. Việc nắm vững các khái niệm và kỹ năng giải bài tập trong mục này sẽ giúp học sinh xây dựng một nền tảng vững chắc cho việc học tập các môn khoa học tự nhiên khác.
Mục 2 bao gồm các nội dung chính sau:
Bài 1: Cho hai điểm A(1; 2; 3) và B(-1; 0; 1). Tìm tọa độ của điểm M sao cho M là trung điểm của đoạn AB.
Lời giải:
Tọa độ trung điểm M của đoạn AB được tính theo công thức:
M = ((xA + xB)/2; (yA + yB)/2; (zA + zB)/2)
Thay tọa độ của A và B vào công thức, ta được:
M = ((1 + (-1))/2; (2 + 0)/2; (3 + 1)/2) = (0; 1; 2)
Vậy tọa độ của điểm M là (0; 1; 2).
Bài 2: Cho vector a = (2; -1; 3) và vector b = (1; 0; -2). Tính tích vô hướng của hai vector a và b.
Lời giải:
Tích vô hướng của hai vector a và b được tính theo công thức:
a.b = xa*xb + ya*yb + za*zb
Thay tọa độ của a và b vào công thức, ta được:
a.b = 2*1 + (-1)*0 + 3*(-2) = 2 + 0 - 6 = -4
Vậy tích vô hướng của hai vector a và b là -4.
Bài 3: Viết phương trình tham số của đường thẳng đi qua điểm A(1; 2; 3) và có vector chỉ phương là vector a = (2; -1; 1).
Lời giải:
Phương trình tham số của đường thẳng đi qua điểm A(x0; y0; z0) và có vector chỉ phương a = (a1; a2; a3) được viết như sau:
{ x = x0 + a1t y = y0 + a2t z = z0 + a3t }
Thay tọa độ của A và vector a vào công thức, ta được:
{ x = 1 + 2t y = 2 - t z = 3 + t }
Vậy phương trình tham số của đường thẳng là { x = 1 + 2t; y = 2 - t; z = 3 + t }.
Để học tốt môn Toán 11, đặc biệt là phần phương pháp tọa độ trong không gian, các em cần:
Giaitoan.edu.vn hy vọng rằng với những lời giải chi tiết và hướng dẫn cụ thể trên đây, các em sẽ tự tin hơn trong việc giải các bài tập Toán 11 tập 1. Chúc các em học tập tốt!