Bài 8.47 trang 90 SGK Toán 11 tập 2 là một bài tập quan trọng trong chương trình học Toán 11. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài 8.47 trang 90 SGK Toán 11 tập 2, giúp các em học sinh nắm vững kiến thức và kỹ năng giải bài tập.
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc nhau và SA = SB = SC = a.
Đề bài
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc nhau và SA = SB = SC = a. Khi đó khoảng cách từ S đến mặt phẳng (ABC) bằng
A. \(\frac{a}{{\sqrt 2 }}\)
B. \(\frac{a}{{\sqrt 3 }}\)
C. \(\frac{a}{2}\)
D. \(\frac{a}{3}\)
Phương pháp giải - Xem chi tiết
Tìm đường thẳng đi qua S và vuông góc (ABC)
Lời giải chi tiết
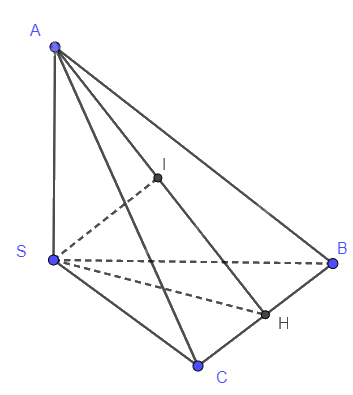
Hạ AH \( \bot \) BC, SI \( \bot \) AH
Ta có: SH \( \bot \) BC, AH \( \bot \) BC suy ra BC \( \bot \) (SAH). Do đó, BC \( \bot \) SI.
Ta có: SI \( \bot \) BC, SI \( \bot \) AH suy ra SI \( \bot \) (ABC)
Suy ra, d(S,(ABC)) = SI
\(\begin{array}{l}BC = \sqrt {S{B^2} + S{C^2}} = \sqrt 2 a\\SH = \frac{{BC}}{2} = \frac{{\sqrt 2 }}{2}a\\\frac{1}{{S{I^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{S{A^2}}} = \frac{1}{{{{\left( {\frac{{\sqrt 2 }}{2}a} \right)}^2}}} + \frac{1}{{{a^2}}}\\ \Leftrightarrow SI = \frac{a}{{\sqrt 3 }}\end{array}\)
Chọn đáp án B.
Bài 8.47 trang 90 SGK Toán 11 tập 2 thuộc chương trình Đại số và Giải tích lớp 11, tập trung vào ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài toán này thường yêu cầu học sinh xác định các điểm cực trị, khoảng đồng biến, nghịch biến và vẽ đồ thị hàm số.
Bài 8.47 thường có dạng như sau: Cho hàm số y = f(x). Hãy tìm:
Tập xác định của hàm số.
Các điểm cực trị của hàm số.
Khoảng đồng biến, nghịch biến của hàm số.
Vẽ đồ thị hàm số.
Để giải bài 8.47 trang 90 SGK Toán 11 tập 2, học sinh cần thực hiện các bước sau:
Tính đạo hàm f'(x): Đây là bước quan trọng nhất để xác định các điểm cực trị và khoảng đồng biến, nghịch biến.
Tìm các điểm cực trị: Giải phương trình f'(x) = 0 để tìm các điểm nghi ngờ là cực trị. Sau đó, xét dấu đạo hàm cấp hai f''(x) để xác định loại cực trị (cực đại hoặc cực tiểu).
Xác định khoảng đồng biến, nghịch biến: Dựa vào dấu của f'(x) để xác định khoảng đồng biến (f'(x) > 0) và khoảng nghịch biến (f'(x) < 0).
Vẽ đồ thị hàm số: Sử dụng các thông tin đã tìm được (tập xác định, điểm cực trị, khoảng đồng biến, nghịch biến) để vẽ đồ thị hàm số.
Giả sử cho hàm số y = x3 - 3x2 + 2.
Bước 1: Tính đạo hàm
y' = 3x2 - 6x
Bước 2: Tìm các điểm cực trị
Giải phương trình y' = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy x = 0 hoặc x = 2
Tính đạo hàm cấp hai:
y'' = 6x - 6
Tại x = 0, y'' = -6 < 0, vậy hàm số đạt cực đại tại x = 0, y = 2.
Tại x = 2, y'' = 6 > 0, vậy hàm số đạt cực tiểu tại x = 2, y = -2.
Bước 3: Xác định khoảng đồng biến, nghịch biến
y' > 0 khi x < 0 hoặc x > 2, vậy hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞).
y' < 0 khi 0 < x < 2, vậy hàm số nghịch biến trên khoảng (0; 2).
Bước 4: Vẽ đồ thị hàm số
(Đồ thị hàm số sẽ được mô tả bằng lời, vì không thể hiển thị hình ảnh trong JSON)
Khi giải bài 8.47 trang 90 SGK Toán 11 tập 2, học sinh cần chú ý:
Kiểm tra kỹ tập xác định của hàm số.
Tính đạo hàm chính xác.
Xét dấu đạo hàm cấp hai cẩn thận để xác định đúng loại cực trị.
Vẽ đồ thị hàm số một cách chính xác, thể hiện đầy đủ các yếu tố quan trọng.
Bài 8.47 trang 90 SGK Toán 11 tập 2 có ứng dụng thực tế trong nhiều lĩnh vực, như:
Kinh tế: Xác định điểm tối ưu trong sản xuất, tiêu thụ.
Vật lý: Tìm điểm cực trị của các hàm số mô tả các hiện tượng vật lý.
Kỹ thuật: Thiết kế các hệ thống tối ưu.
Việc nắm vững kiến thức và kỹ năng giải bài 8.47 trang 90 SGK Toán 11 tập 2 là rất quan trọng đối với học sinh lớp 11, giúp các em có nền tảng vững chắc để học tập các môn học khác và chuẩn bị cho kỳ thi THPT Quốc gia.
Giaitoan.edu.vn hy vọng với lời giải chi tiết và phương pháp giải tối ưu này, các em học sinh sẽ tự tin hơn trong việc giải quyết các bài toán tương tự.