Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Trong bài viết này, chúng ta sẽ cùng nhau Giải mục 1 trang 80 SGK Toán 11 tập 2, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, giúp bạn tiết kiệm thời gian và đạt kết quả tốt nhất.
Viết công thức tính thể tích khối lăng trụ đứng tam giác (Hình 8.68)
Viết công thức tính thể tích khối lăng trụ đứng tam giác (Hình 8.68) và khối lăng trụ đứng tứ giác (Hình 8.69) theo diện tích đáy S và đường cao h của nó.
Phương pháp giải:
V = S.h
Lời giải chi tiết:
Công thức tính thể tích khối lăng trụ đứng: V = S.h
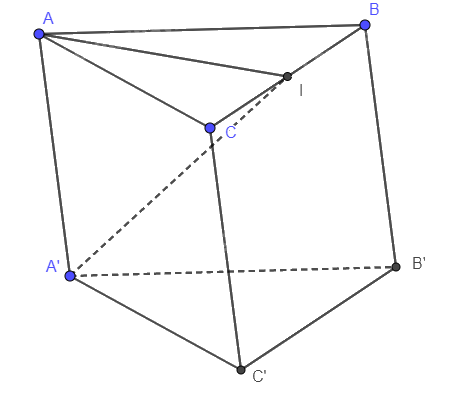
Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a , góc giữa cạnh bên và mặt đáy bằng 300. Hình chiếu của A’ trên (ABC) là trung điểm I của cạnh BC. Tính thể tích khối lăng trụ này.
Phương pháp giải:
Công thức tính thể tích khối lăng trụ: V = S.h
S: diện tích đáy, h: chiều cao
Lời giải chi tiết:

Gọi I là trung điểm BC
\(AI = \sqrt {A{C^2} - I{C^2}} = \sqrt {{a^2} - {{\left( {\frac{1}{2}a} \right)}^2}} = \frac{{\sqrt 3 }}{2}a\)
Tam giác AB đều nên AI vuông góc với BC hay AI vuông góc với (ABC)
Suy ra \(\widehat {\left( {AA',\left( {ABC} \right)} \right)} = \widehat {A'AI} = {30^0}\)
I là hình chiếu của A’ trên (ABC) nên A’I vuông góc với BC
Suy ra tam giác A’AI vuông tại I có:
\(\tan {30^0} = \frac{{A'I}}{{AI}} = \frac{{A'I}}{{\frac{{\sqrt 3 }}{2}a}} \Rightarrow A'I = \frac{1}{2}a\)
\(V = {S_{\Delta ABC}}.A'I = \frac{1}{2}AI.BC.A'I = \frac{1}{2}.\frac{{\sqrt 3 }}{2}a.a.\frac{1}{2}a = \frac{{\sqrt 3 }}{8}{a^3}\)
Mục 1 trang 80 SGK Toán 11 tập 2 thường xoay quanh các kiến thức về đạo hàm của hàm số, bao gồm các dạng bài tập tính đạo hàm, ứng dụng đạo hàm để khảo sát hàm số và giải các bài toán liên quan đến cực trị, giá trị lớn nhất, giá trị nhỏ nhất của hàm số. Việc nắm vững các công thức và quy tắc đạo hàm là yếu tố then chốt để giải quyết các bài tập trong mục này.
Để giúp các em học sinh hiểu rõ hơn về nội dung và phương pháp giải các bài tập trong mục 1 trang 80 SGK Toán 11 tập 2, chúng ta sẽ đi vào phân tích từng bài tập cụ thể.
Bài tập này yêu cầu học sinh vận dụng các quy tắc đạo hàm cơ bản như đạo hàm của tổng, hiệu, tích, thương, đạo hàm của hàm hợp để tính đạo hàm của các hàm số đã cho. Ví dụ:
Khi giải bài tập này, cần chú ý đến việc xác định đúng các quy tắc đạo hàm áp dụng và thực hiện các phép tính một cách cẩn thận.
Bài tập này yêu cầu học sinh tính đạo hàm của hàm số tại một điểm cụ thể. Để làm được điều này, cần thực hiện các bước sau:
Ví dụ: Tìm đạo hàm của hàm số y = x2 + 3x - 2 tại x = 1.
Bài tập này yêu cầu học sinh sử dụng đạo hàm để xác định các khoảng đơn điệu, cực trị, điểm uốn và vẽ đồ thị của hàm số. Các bước thực hiện như sau:
Ngoài các dạng bài tập đã nêu trên, còn có một số dạng bài tập khác thường xuất hiện trong mục 1 trang 80 SGK Toán 11 tập 2, như:
Để giải quyết tốt các bài tập trong mục 1 trang 80 SGK Toán 11 tập 2, các em học sinh cần:
Hy vọng rằng với những hướng dẫn chi tiết và cụ thể trên, các em học sinh sẽ tự tin hơn trong việc Giải mục 1 trang 80 SGK Toán 11 tập 2. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!