Bài 5.5 trang 134 SGK Toán 11 tập 1 thuộc chương trình học Toán 11, tập trung vào việc giải các phương trình lượng giác cơ bản. Bài học này giúp học sinh rèn luyện kỹ năng biến đổi lượng giác và áp dụng các công thức để tìm nghiệm của phương trình.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cùng với các ví dụ minh họa để bạn có thể nắm vững kiến thức và tự tin giải các bài tập tương tự.
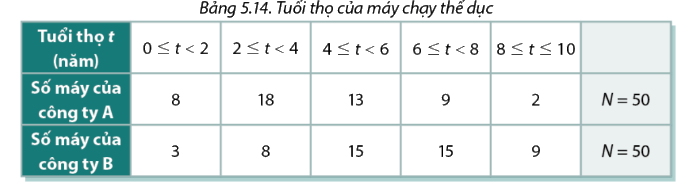
Người ta tiến hành khảo sát tuổi thọ của một số máy chạy thể dục do hai công ty A và B sản xuất . Kết quả được tóm tắt trong Bảng 5.14 .
Đề bài
Người ta tiến hành khảo sát tuổi thọ của một số máy chạy thể dục do hai công ty A và B sản xuất . Kết quả được tóm tắt trong Bảng 5.14 . Ước tính tuổi thọ trung bình của các máy chạy thể dục được sản xuất bởi mỗi công ty. Có thể dự đoán là sản phẩm của công ty nào có độ bền cao hơn?
Phương pháp giải - Xem chi tiết
Lập bảng mẫu số liệu ghép nhóm của từng công ty sau đó tính giá trị trung bình và thực hiện so sánh.
Lời giải chi tiết
Bảng mẫu số liệu ghép nhóm công ty A
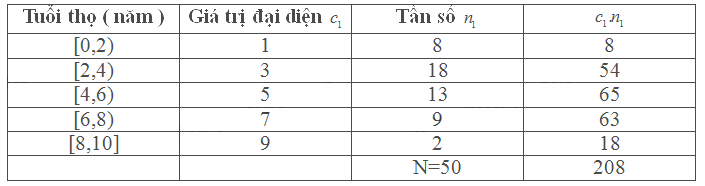
Tuổi thọ trung bình của máy tập thể dục công ty A là: \(\mathop {{x_A}}\limits^\_ = \frac{{208}}{{50}} = 4,16\)
Bảng mẫu số liệu ghép nhóm công ty B
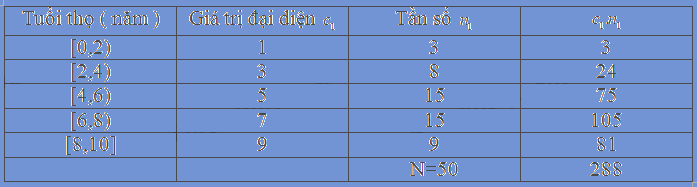
Tuổi thọ trung bình máy tập thể dục công ty B là: \(\mathop {{x_B}}\limits^\_ = \frac{{288}}{{50}} = 5,76\)
Do \({x_B} > {x_A}\) nên tuổi thọ máy công ty B cao hơn công ty A.
Bài 5.5 trang 134 SGK Toán 11 tập 1 yêu cầu giải các phương trình lượng giác. Để giải quyết bài toán này, chúng ta cần nắm vững các kiến thức cơ bản về lượng giác, bao gồm các công thức biến đổi lượng giác, các giá trị lượng giác của các góc đặc biệt và các phương pháp giải phương trình lượng giác.
Bài 5.5 thường bao gồm các phương trình lượng giác có dạng:
Trong đó, 'a' là một số thực. Việc giải các phương trình này đòi hỏi chúng ta phải biết cách xác định các nghiệm thuộc khoảng [0, 2π) và sau đó tìm các nghiệm tổng quát.
Để giải phương trình lượng giác, chúng ta có thể sử dụng các phương pháp sau:
Ví dụ 1: Giải phương trình sin(x) = 1/2
Ta có sin(x) = 1/2. Từ đường tròn lượng giác, ta thấy x = π/6 và x = 5π/6 là các nghiệm thuộc khoảng [0, 2π). Vậy nghiệm tổng quát của phương trình là:
x = π/6 + k2π
x = 5π/6 + k2π (k ∈ Z)
Ví dụ 2: Giải phương trình cos(x) = -√2/2
Ta có cos(x) = -√2/2. Từ đường tròn lượng giác, ta thấy x = 3π/4 và x = 5π/4 là các nghiệm thuộc khoảng [0, 2π). Vậy nghiệm tổng quát của phương trình là:
x = 3π/4 + k2π
x = 5π/4 + k2π (k ∈ Z)
Để củng cố kiến thức, bạn có thể tự giải các bài tập tương tự sau:
Bài 5.5 trang 134 SGK Toán 11 tập 1 là một bài học quan trọng giúp học sinh nắm vững kiến thức về phương trình lượng giác. Bằng cách áp dụng các phương pháp giải và luyện tập thường xuyên, bạn có thể tự tin giải quyết các bài toán liên quan đến chủ đề này. giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán.