Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Toán 11 tập 2. Mục 2 của chương trình Toán 11 tập 2 tập trung vào các kiến thức quan trọng về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế.
Chúng tôi hiểu rằng việc tự học và làm bài tập có thể gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn bộ giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải quyết mọi bài tập.
Cho hình hộp \(ABCD.A'B'C'D'\) có \(AA' \bot AB\) và \(A'A \bot AD\) (Hình 8.8)
Cho hình hộp \(ABCD.A'B'C'D'\) có \(AA' \bot AB\) và \(A'A \bot AD\) (Hình 8.8)
a) Mặt phẳng \(\left( {ABCD} \right)\) có vuông góc với \(A'A\) không? Vì sao?
b) Gọi \(\left( \alpha \right)\) là mặt phẳng qua \(A\) và vuông góc với \(A'A\). Hãy tìm giao tuyến của \(\left( \alpha \right)\) với các mặt phẳng \(\left( {AA'B'B} \right)\) và \(\left( {A'ADD'} \right)\). Từ đó tìm mối quan hệ giữa \(\left( \alpha \right)\) và mặt phẳng \(\left( {ABCD} \right)\)
Phương pháp giải:
a) Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng nằm trong một mặt phẳng thì nó vuông góc với mặt phẳng ấy.
b) Tìm 2 điểm chung của 2 mặt phẳng là ta tìm được giao tuyến của chúng.
Lời giải chi tiết:
a) Vì \(\left\{ \begin{array}{l}AA' \bot AB\\AA' \bot AD\\AB \cap AD = \left\{ A \right\}\end{array} \right. \Rightarrow AA' \bot \left( {ABCD} \right)\)
b) Vì \(\left( \alpha \right)\) đi qua \(A\) và vuông góc với \(AA'\)\( \Rightarrow \)\(\left( \alpha \right)\) trùng với \(\left( {ABCD} \right)\)
Do đó \(\left( \alpha \right) \cap \left( {AA'B'B} \right) = AB\)
\(\left( \alpha \right) \cap \left( {AA'D'D} \right) = AD\)
Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật và \(SA\) vuông góc với đáy. Gọi \(B',C',D'\) lần lượt là hình chiếu của \(A\) trên các cạnh \(SB,SC,SD\). Chứng minh \(SC \bot \left( {AB'D'} \right)\) và \(AB',AC',AD'\) cùng nằm trên một mặt phẳng.
Phương pháp giải:
Chứng minh \(AB' \bot \left( {SBC} \right) \Rightarrow AB' \bot SC\)
Chứng minh \(AD' \bot \left( {SCD} \right) \Rightarrow AD' \bot SC\)
Chứng minh ba đường thẳng \(AB',AC',AD'\) cùng vuông góc với một đường thẳng
Lời giải chi tiết:

+) Ta có \(BC \bot AB\) (Vì \(ABCD\) là hình chữ nhật)
\(BC \bot SA\) vì \(SA \bot \left( {ABCD} \right)\)
Vì \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right)\)
Mà \(AB' \subset \left( {SAB} \right) \Rightarrow AB' \bot BC\)
Vì \(\left\{ \begin{array}{l}AB' \bot SB\\AB' \bot BC\end{array} \right. \Rightarrow AB' \bot \left( {SBC} \right) \Rightarrow AB' \bot SC\)
+) Ta có \(DC \bot AD\) (Vì \(ABCD\) là hình chữ nhật)
\(DC \bot SA\) vì \(SA \bot \left( {ABCD} \right)\)
Vì \(\left\{ \begin{array}{l}DC \bot AD\\DC \bot SA\end{array} \right. \Rightarrow DC \bot \left( {SAD} \right)\)
Mà \(AD' \subset \left( {SAD} \right) \Rightarrow AD' \bot DC\)
Vì \(\left\{ \begin{array}{l}AD' \bot SD\\AD' \bot DC\end{array} \right. \Rightarrow AD' \bot \left( {SDC} \right) \Rightarrow AD' \bot SC\)
Vì \(\left\{ \begin{array}{l}SC \bot AB'\\SC \bot AD'\end{array} \right. \Rightarrow SC \bot \left( {AB'D'} \right)\)
+) Ta có \(AB',AC',AD'\) cùng vuông góc với \(SC\) suy ra chúng cùng nằm trên mặt phẳng. Mà \(SC \bot \left( {AB'D'} \right)\) nên mặt phẳng đó là \(\left( {AB'D'} \right)\)
Cho hai đường thẳng \(a,b\) song song với nhau và mặt phẳng \(\left( \alpha \right)\) vuông góc với \(a\) (Hình 8.13). Hỏi \(\left( \alpha \right)\) có vuông góc với \(b\) không? Vì sao?

Phương pháp giải:
Sử dụng từ vuông góc đến song song
Lời giải chi tiết:
Ta có \(\left\{ \begin{array}{c}a//b\\a \bot \left( \alpha \right)\end{array} \right. \Rightarrow b \bot \left( \alpha \right)\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông, \(SA\) vuông góc với mặt phẳng đáy. Gọi \(H,K\) lần lượt là hình chiếu của \(A\) trên \(SB,SD\). Chứng minh \(HK \bot \left( {SAC} \right)\)
Phương pháp giải:
Chứng minh \(BD \bot \left( {SAC} \right)\) và \(HK//BD\). Từ đó suy ra \(HK \bot \left( {SAC} \right)\)
Lời giải chi tiết:

Ta có \(BD \bot AC\) (vì \(ABCD\) là hình vuông)
\(BD \bot SA\) vì \(SA \bot \left( {ABCD} \right)\)
Ta có \(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SA\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right)\) \(\left( 1 \right)\)
Xét \(\Delta SAB\) có \(AH \bot SB\)\( \Rightarrow \frac{{SH}}{{SB}} = \frac{{SH.SB}}{{S{B^2}}} = \frac{{S{A^2}}}{{S{B^2}}}\)
Xét \(\Delta SAD\) có \(AK \bot SD\)\( \Rightarrow \frac{{SK}}{{SD}} = \frac{{SK.SD}}{{S{D^2}}} = \frac{{S{A^2}}}{{SD}}\)
Mà \(SB = SD\)\( \Rightarrow \frac{{SH}}{{SB}} = \frac{{SK}}{{SD}} \Rightarrow HK//BD\) (áp dụng định lí Ta – lét) \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), suy ra \(HK \bot \left( {SAC} \right)\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi, \(O\) là giao điểm của \(AC\) và \(DB\), \(SA = SC\), \(SB = SD\). Gọi \(I,K\) lần lượt là trung điểm của \(AB\) và \(BC\). Mặt phẳng \(\left( \alpha \right)\) chứa \(IK\) và song song với \(SO\). Chứng minh \(\left( \alpha \right) \bot BD\)
Phương pháp giải:
Chứng minh \(\left( \alpha \right)//\left( {SAC} \right)\)
Chứng minh \(BD \bot \left( {SAC} \right)\) từ đó suy ra \(BD \bot \left( \alpha \right)\)
Lời giải chi tiết:

Ta có \(IK//AC\) vì \(IK\) là đường trung bình của \(\Delta SAC\)\(\left\{ \begin{array}{l}IK//AC\\IK \subset \left( \alpha \right)\end{array} \right. \Rightarrow AC//\left( \alpha \right)\)
Vì \(\left\{ \begin{array}{l}SO//\left( \alpha \right)\\AC//\left( \alpha \right)\end{array} \right. \Rightarrow \left( {SAC} \right)//\left( \alpha \right)\)
Vì \(ABCD\) là hình thoi tâm \(O\) nên \(AC \bot BD\) tại \(O\)
Xét \(\Delta SBD\) có \(SB = SD\) và \(O\) là trung điểm của \(BD\)\( \Rightarrow SO \bot BD\)
Vì \(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SO\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right)\)
Mà \(\left( \alpha \right)//\left( {SAC} \right) \Rightarrow \left( \alpha \right) \bot BD\)
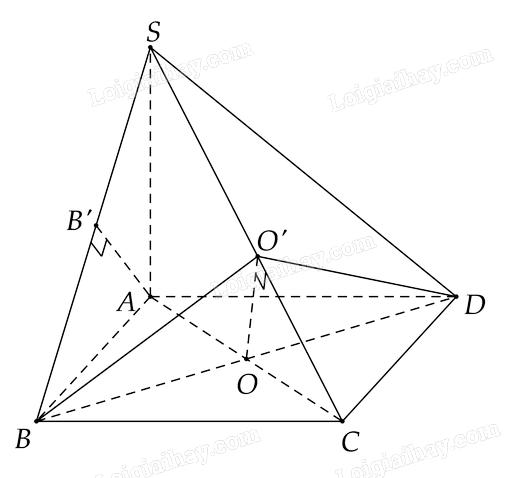
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông, \(SA \bot \left( {ABCD} \right)\). Gọi \(O\) là giao điểm của \(AC\) và \(BD\), \(B'\) là hình chiếu của \(A\) trên \(SB\), \(O'\) là hình chiếu của \(O\) trên \(SC\). Chứng minh \(AB'//\left( {O'BD} \right)\)
Phương pháp giải:
\(AB'//\left( {O'BD} \right)\)
Lời giải chi tiết:

Ta có \(AC \bot BD\) (giả thiết)
Vì \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot BD\)
Vì \(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SA\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow BD \bot SC\)
Vì \(\left\{ \begin{array}{l}OO' \bot SC\,\,\left( {gt} \right)\\BD \bot SC\end{array} \right. \Rightarrow SC \bot \left( {O'BD} \right)\)
+) Ta có \(\left\{ \begin{array}{l}BC \bot AB\,\,\left( {gt} \right)\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AB'\)
Ta có \(\left\{ \begin{array}{l}AB' \bot BC\\AB' \bot SB\end{array} \right. \Rightarrow AB' \bot \left( {SBC} \right) \Rightarrow AB' \bot SC\)
Vì \(\left\{ \begin{array}{l}AB' \bot SC\\\left( {O'BD} \right) \bot SC\end{array} \right. \Rightarrow AB'//\left( {O'BD} \right)\)
Mục 2 của SGK Toán 11 tập 2 thường xoay quanh các chủ đề về đạo hàm của hàm số lượng giác, đạo hàm của hàm hợp và các ứng dụng của đạo hàm trong việc khảo sát hàm số. Việc nắm vững các công thức và quy tắc đạo hàm là nền tảng để giải quyết các bài tập trong mục này.
Các công thức đạo hàm cơ bản của các hàm số lượng giác cần được ghi nhớ:
Khi đạo hàm các hàm số lượng giác phức tạp, cần sử dụng quy tắc chuỗi (chain rule) để tính đạo hàm.
Quy tắc chuỗi là một công cụ mạnh mẽ để tính đạo hàm của hàm hợp. Nếu y = f(u) và u = g(x), thì dy/dx = (dy/du) * (du/dx). Ví dụ, để tính đạo hàm của sin(x2), ta có u = x2 và y = sin(u). Vậy, dy/dx = cos(u) * 2x = cos(x2) * 2x.
Đạo hàm đóng vai trò quan trọng trong việc khảo sát hàm số, bao gồm:
Dưới đây là giải chi tiết một số bài tập tiêu biểu trong mục 2, trang 56, 57, 58, 59, 60 SGK Toán 11 tập 2:
Giải: Sử dụng quy tắc chuỗi, ta có u = 2x và y = sin(u). Vậy, dy/dx = cos(u) * 2 = 2cos(2x).
Giải: Sử dụng quy tắc chuỗi, ta có u = cos(x) và y = u2. Vậy, dy/dx = 2u * (-sin(x)) = -2cos(x)sin(x) = -sin(2x).
Giải: Tính đạo hàm y' = 3x2 - 6x. Giải phương trình y' = 0, ta được x = 0 và x = 2. Tính đạo hàm bậc hai y'' = 6x - 6. Tại x = 0, y'' = -6 < 0, hàm số đạt cực đại tại x = 0. Tại x = 2, y'' = 6 > 0, hàm số đạt cực tiểu tại x = 2.
Giải: Tính đạo hàm y' = 4x3 - 8x. Giải phương trình y' = 0, ta được x = 0, x = √2, x = -√2. Tính đạo hàm bậc hai y'' = 12x2 - 8. Xác định các điểm cực trị và khoảng đơn điệu của hàm số.
Giải: Chia cả hai vế cho cos(x) (với cos(x) ≠ 0), ta được tan(x) = 1. Vậy, x = π/4 + kπ, k ∈ Z.
Để học tốt và giải quyết hiệu quả các bài tập trong mục 2, bạn nên:
Giaitoan.edu.vn hy vọng rằng với bộ giải chi tiết này, bạn sẽ tự tin hơn trong việc học tập và giải quyết các bài tập Toán 11 tập 2. Chúc bạn học tốt!