Bài 8.9 trang 63 SGK Toán 11 tập 2 là một bài tập quan trọng trong chương trình học Toán 11. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu Bài 8.9 trang 63 SGK Toán 11 tập 2, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
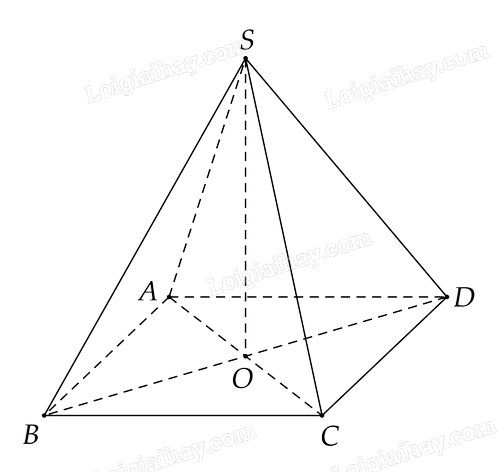
Cho hình chóp S.ABCD có đáy ABCD là hình thoi, O là giao điểm của AC và BD và SA=SC, SB= SD.
Đề bài
Cho hình chóp S.ABCD có đáy ABCD là hình thoi, O là giao điểm của AC và BD và SA=SC, SB= SD. Chứng minh \(BC \bot SO\) và \(SC \bot BD\).
Phương pháp giải - Xem chi tiết
Chứng minh \(SO \bot AC,SO \bot BD\) từ đó suy ra \(SO \bot \left( {ABCD} \right)\) và suy ra \(SO \bot BC\)
Chứng minh \(BD \bot \left( {SAC} \right)\) từ đó suy ra \(BD \bot SC\)
Lời giải chi tiết
+) Vì \(ABCD\) là hình thoi nên \(AC \bot BD\) tại trung điểm \(O\) của mỗi đường
Vì \(SA = SC \Rightarrow \Delta SAC\) cân tại \(S\) và \(O\) là trung điểm \(AC\) nên \(SO \bot AC\)
Vì \(SB = SD\)\( \Rightarrow \Delta SBD\) cân tại \(S\) và \(O\) là trung điểm \(BD\) nên \(SO \bot BD\)
Ta có \(\left\{ \begin{array}{l}SO \bot AC\\SO \bot BD\end{array} \right. \Rightarrow SO \bot \left( {ABCD} \right) \Rightarrow SO \bot BC\)
+) Vì \(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot BD\)
Ta có \(\left\{ \begin{array}{l}SO \bot BD\\AC \bot BD\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow BD \bot SC\)
Bài 8.9 trang 63 SGK Toán 11 tập 2 thuộc chương trình học Toán 11, tập trung vào ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Bài toán này thường yêu cầu học sinh xác định các yếu tố như khoảng đồng biến, nghịch biến, cực trị của hàm số để tìm ra giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng cho trước.
Trước khi bắt đầu giải bài toán, điều quan trọng là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong Bài 8.9 trang 63, học sinh cần xác định hàm số, khoảng xét hàm số và mục tiêu của bài toán (ví dụ: tìm giá trị lớn nhất, giá trị nhỏ nhất).
Để giải Bài 8.9 trang 63 SGK Toán 11 tập 2, học sinh có thể áp dụng các bước sau:
Giả sử bài toán yêu cầu tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = x3 - 3x2 + 2 trên khoảng [0, 3].
Vậy, giá trị lớn nhất của hàm số trên khoảng [0, 3] là 2 (tại x = 0 và x = 3) và giá trị nhỏ nhất là -2 (tại x = 2).
Để nắm vững phương pháp giải bài toán ứng dụng đạo hàm, học sinh nên luyện tập thêm với các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp học sinh hiểu rõ hơn về các khái niệm và kỹ năng cần thiết để giải quyết các bài toán phức tạp hơn.
Bài 8.9 trang 63 SGK Toán 11 tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng ứng dụng đạo hàm để giải quyết các bài toán thực tế. Bằng cách nắm vững phương pháp giải và luyện tập thường xuyên, học sinh có thể tự tin làm bài tập và đạt kết quả tốt trong môn Toán 11.