Bài 4.11 trang 100 SGK Toán 11 tập 1 là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về hàm số bậc hai và phương trình bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.11 trang 100 SGK Toán 11 tập 1, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Cho hình chóp S.ABCD có đáy là tứ giác ABCD. Gọi M, N lần lượt là trọng tâm của các tam giác SAB, SAD. Lấy I là trung điểm của đoạn BC.
Đề bài
Cho hình chóp S.ABCD có đáy là tứ giác ABCD. Gọi M, N lần lượt là trọng tâm của các tam giác SAB, SAD. Lấy I là trung điểm của đoạn BC.
a) Chứng minh rằng MN // BD.
b) Gọi L, H lần lượt là giao điểm của SB, SD với mặt phẳng (MNI). Chứng minh rằng LH // BD.
Phương pháp giải - Xem chi tiết
a) Áp dụng định lý: Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.
b) - Cách tìm giao điểm của một đường thẳng a với một mặt phẳng (P):
+ Bước 1: Tìm \(\left( Q \right) \supset a\). Tìm \(d = \left( P \right) \cap \left( Q \right)\)
+ Bước 2: Tìm \(I = a \cap d\). I chính là giao điểm của a và (P).
- Áp dụng hệ quả: Nếu 2 mặt phẳng phân biệt lần lượt chứa 2 đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với 2 đường thẳng đó hoặc trùng với một trong 2 đường thẳng đó
Lời giải chi tiết
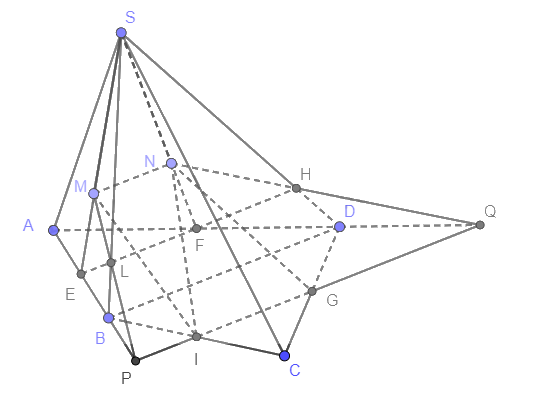
a) Gọi E là trung điểm của AB, F là trung điểm AD
\( \Rightarrow SM = \frac{2}{3}SE,SN = \frac{2}{3}SF\)
Xét tam giác SEF có: \(\frac{{SM}}{{SE}} = \frac{{SN}}{{SF}} = \frac{2}{3} \Rightarrow MN/EF\)
Xét tam giác ABD có E, F lần lượt là trung điểm của AB, AD nên \(EF//BD\)
Vậy \(MN//BD\).
b) Trong (ABCD), gọi \(G\left( {G \in CD} \right)\) sao cho \(IG//BD\), gọi \(P = AB \cap IG,Q = AD \cap IG\).
Mở rộng (MNI) thành (MNQP)
Ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}M \in SE \subset \left( {SAB} \right)\\P \in AB \subset \left( {SAB} \right)\end{array} \right. \Rightarrow MP \subset \left( {SAB} \right)\\MP \subset \left( {MNQP} \right)\\ \Rightarrow MP = \left( {SAB} \right) \cap \left( {MNQP} \right)\end{array}\)
Gọi \(L = SB \cap MP\)\( \Rightarrow L = SB \cap \left( {MNQP} \right)\)(1)
\(\begin{array}{l}\left\{ \begin{array}{l}N \in SF \subset \left( {SAD} \right)\\Q \in AD \subset \left( {SAD} \right)\end{array} \right. \Rightarrow NQ \subset \left( {SAD} \right)\\NQ \subset \left( {MNQP} \right)\\ \Rightarrow NQ = \left( {SAD} \right) \cap \left( {MNQP} \right)\end{array}\)
Gọi \(H = SD \cap NQ\)\( \Rightarrow H = SD \cap \left( {MNQP} \right)\)(2)
Từ (1) và (2) suy ra \(LH = \left( {SBD} \right) \cap \left( {MNQP} \right)\)
Mà \(BD//MN\) (phần a)
\( \Rightarrow LH//BD//MN\).
Bài 4.11 trang 100 SGK Toán 11 tập 1 yêu cầu học sinh giải một bài toán thực tế liên quan đến hàm số bậc hai. Để giải bài toán này, chúng ta cần nắm vững các kiến thức sau:
Nội dung bài toán: (Giả sử bài toán là tìm tập xác định của hàm số)
Cho hàm số f(x) = (x-2)/(x^2 - 4x + 3). Tìm tập xác định của hàm số.
Để tìm tập xác định của hàm số f(x) = (x-2)/(x^2 - 4x + 3), ta cần tìm các giá trị của x sao cho mẫu số khác 0.
x^2 - 4x + 3 ≠ 0
Giải phương trình x^2 - 4x + 3 = 0, ta được:
(x-1)(x-3) = 0
Vậy x = 1 hoặc x = 3
Do đó, tập xác định của hàm số f(x) là D = R \ {1; 3}.
Bài toán này yêu cầu học sinh phải hiểu rõ điều kiện xác định của hàm số hữu tỉ. Để giải bài toán tương tự, học sinh cần:
Ngoài ra, học sinh cũng cần rèn luyện kỹ năng giải phương trình bậc hai để có thể giải quyết các bài toán phức tạp hơn.
Kết luận:
Bài 4.11 trang 100 SGK Toán 11 tập 1 là một bài tập cơ bản nhưng quan trọng, giúp học sinh củng cố kiến thức về hàm số bậc hai và phương trình bậc hai. Việc giải bài tập này một cách chính xác và hiểu rõ bản chất sẽ giúp học sinh tự tin hơn trong quá trình học tập và làm bài kiểm tra.
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết này sẽ giúp các em học sinh hiểu rõ hơn về bài toán và có thêm động lực để học tập tốt môn Toán.
Lưu ý: Đây chỉ là một ví dụ về lời giải cho bài toán. Tùy thuộc vào nội dung cụ thể của bài toán, cách giải có thể khác nhau. Học sinh nên tự mình suy nghĩ và tìm tòi để hiểu rõ hơn về bài toán.
Để nắm vững kiến thức Toán 11, các em nên thường xuyên luyện tập các bài tập trong SGK và các tài liệu tham khảo khác. Ngoài ra, các em cũng có thể tham gia các khóa học Toán online tại giaitoan.edu.vn để được hướng dẫn và giải đáp thắc mắc bởi các giáo viên giàu kinh nghiệm.