Chào mừng bạn đến với chuyên mục Lý thuyết Logarit - SGK Toán 11 của giaitoan.edu.vn. Logarit là một khái niệm quan trọng trong chương trình Toán học, đặc biệt là ở lớp 11. Việc nắm vững lý thuyết Logarit sẽ giúp bạn giải quyết các bài toán một cách nhanh chóng và chính xác.
Chúng tôi cung cấp đầy đủ các kiến thức về Logarit, từ định nghĩa, tính chất, đến các công thức và ứng dụng thực tế.
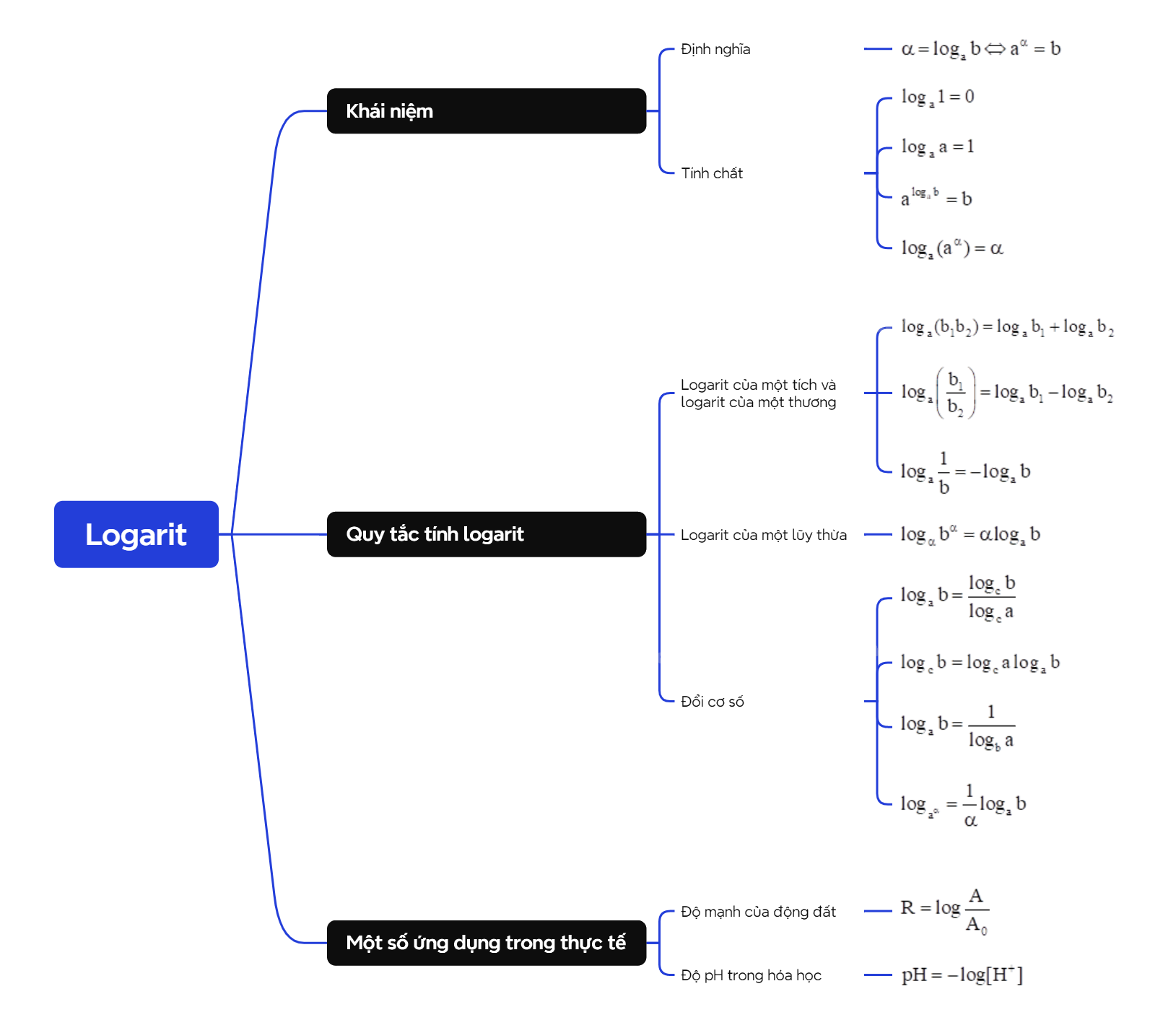
A. Lý thuyết 1. Khái niệm logarit a) Định nghĩa
A. Lý thuyết
1. Khái niệm logarit
a) Định nghĩa
Cho hai số thực dương a, b và a khác 1. Số thực \(\alpha \) thỏa mãn đẳng thức \({a^\alpha } = b\) được gọi là logarit cơ số a của b, kí hiệu \({\log _a}b\), nghĩa là \(\alpha = {\log _a}b \Leftrightarrow {a^\alpha } = b\). |
Lưu ý:
- Không tồn tại logarit của số âm và số 0.
- Logarit cơ số 10 của một số dương b là logarit thập phân của b, ký hiệu logb hay lgb.
- Logarit cơ số e của một số dương b là logarit tự nhiên (hay logarit Nê-pe) của b, ký hiệu lnb.
b) Tính chất
Cho a là một số dương khác 1, b là một số dương và số thực \(\alpha \). +) \({\log _a}1 = 0\) +) \({\log _a}a = 1\) +) \({a^{{{\log }_a}b}} = b\) +) \({\log _a}({a^\alpha }) = \alpha \) |
2. Quy tắc tính logarit
a) Logarit của một tích và logarit của một thương
Cho ba số dương a, \({b_1}\), \({b_2}\) và \(a \ne 1\). Khi đó: +) \({\log _a}({b_1}{b_2}) = {\log _a}{b_1} + {\log _a}{b_2}\) +) \({\log _a}\left( {\frac{{{b_1}}}{{{b_2}}}} \right) = {\log _a}{b_1} - {\log _a}{b_2}\) |
Lưu ý: \({\log _a}\frac{1}{b} = - {\log _a}b\).
b) Logarit của một lũy thừa
Cho hai số dương a, b với \(a \ne 1\). Với mọi \(\alpha \), ta có: \({\log _\alpha }{b^\alpha } = \alpha {\log _a}b\). |
Lưu ý : \({\log _a}\sqrt[n]{b} = \frac{1}{n}{\log _a}b\) \((n \in \mathbb{N},n \ge 2)\).
c) Đổi cơ số
Cho ba số thực dương a, b, c với \(a \ne 1\). Khi đó: \({\log _a}b = \frac{{{{\log }_c}b}}{{{{\log }_c}a}}\) hay \({\log _c}b = {\log _c}a{\log _a}b\). |
Lưu ý:
- Với a, b là hai số thực dương khác 1, ta có \({\log _a}b = \frac{1}{{{{\log }_b}a}}\) hay \({\log _a}b.{\log _b}a = 1\).
- Với a là một số dương khác 1, b là số thực dương và \(\alpha \ne 0\), ta có \({\log _{{a^\alpha }}} = \frac{1}{\alpha }{\log _a}b\).
3. Một số ứng dụng trong thực tế
a) Độ mạnh của động đất
\(R = \log \frac{A}{{{A_0}}}\) (độ Richter).
b) Độ pH trong hóa học
\(pH = - \log [{H^ + }]\).
B. Bài tập
Bài 1: Tính:
a) \({\log _2}8\).
b) \({\log _{\frac{1}{2}}}4\).
c) \({\log _3}\frac{1}{{27}}\).
Giải:
a) \({\log _2}8 = 3\) vì \({2^3} = 8\).
b) \({\log _{\frac{1}{2}}}4 = - 2\) vì \({\left( {\frac{1}{2}} \right)^{ - 2}} = 4\).
c) \({\log _3}\frac{1}{{27}} = - 3\) vì \({3^{ - 3}} = \frac{1}{{27}}\).
Bài 2: Tính:
a) \({3^{2{{\log }_3}5}}\).
b) \({\log _{\frac{1}{2}}}\sqrt {\frac{1}{8}} \).
Giải:
a) \({3^{2{{\log }_3}5}} = {({3^{{{\log }_3}5}})^2} = {5^2} = 25\).
b) \({\log _{\frac{1}{2}}}\sqrt {\frac{1}{8}} = {\log _{\frac{1}{2}}}{\left( {\frac{1}{2}} \right)^{\frac{3}{2}}} = \frac{3}{2}\).
Bài 3: Không sử dụng máy tính cầm tay, tính các giá trị biểu thức sau:
a) \(A = {\log _6}3 + {\log _6}12\).
b) \(B = {\log _7}21 - {\log _7}147\).
Giải:
a) \(A = {\log _6}3 + {\log _6}12 = {\log _6}(3.12) = {\log _6}(36) = 2\).
b) \(B = {\log _7}21 - {\log _7}147 = {\log _7}\frac{{21}}{{147}} = {\log _7}\frac{1}{7} = {\log _7}{7^{ - 1}} = - 1\).
Bài 4: Cho \(a = {\log _3}x\); \(b = {\log _3}y\); \(c = {\log _3}z\). Tính \({\log _3}\left( {\frac{{\sqrt[3]{x}}}{{{y^2}.{z^4}}}} \right)\) theo a, b, c.
Giải:
\({\log _3}\left( {\frac{{\sqrt[3]{x}}}{{{y^2}.{z^4}}}} \right) = {\log _3}\sqrt[3]{x} - ({\log _3}{y^2} + {\log _3}{z^4}) = \frac{1}{3}{\log _3}x - (2{\log _3}y + 4{\log _3}z) = \frac{1}{3}a - 2b - 4c\).
Bài 5:
a) Không sử dụng máy tính cầm tay, tính giá trị biểu thức \({\log _{\frac{1}{4}}}({\log _3}4.{\log _2}3)\).
b) Cho \(\alpha = {\log _3}45\). Tính \({\log _{45}}5\) theo a.
Giải:
a) \({\log _{\frac{1}{4}}}({\log _3}4.{\log _2}3) = {\log _{\frac{1}{4}}}(2{\log _3}2.{\log _2}3) = {\log _{\frac{1}{4}}}2 = {\log _{{2^{ - 2}}}}2 = - \frac{1}{2}\).
b) Ta có \(\alpha = {\log _3}45 = {\log _3}({3^2}.5) = 2{\log _3}3 + {\log _3}5 = 2 + {\log _3}5\).
Suy ra \({\log _3}5 = \alpha - 2\). Vậy \({\log _{45}}5 = \frac{{{{\log }_3}5}}{{{{\log }_3}45}} = \frac{{\alpha - 2}}{\alpha }\).
Logarit là một khái niệm toán học quan trọng, đóng vai trò nền tảng trong nhiều lĩnh vực khác nhau, từ khoa học tự nhiên đến kỹ thuật. Trong chương trình SGK Toán 11, việc hiểu rõ lý thuyết logarit là điều kiện tiên quyết để giải quyết các bài toán phức tạp và xây dựng nền tảng vững chắc cho các kiến thức toán học nâng cao.
Logarit của một số dương b theo cơ số a (với a > 0 và a ≠ 1) là số x sao cho ax = b. Ký hiệu: logab = x.
Logarit có nhiều tính chất quan trọng giúp đơn giản hóa các phép tính và giải quyết bài toán. Dưới đây là một số tính chất cơ bản:
Có một số dạng logarit đặc biệt thường gặp:
Logarit và hàm mũ là hai khái niệm nghịch đảo của nhau. Nếu ax = b thì logab = x và ngược lại.
Logarit có nhiều ứng dụng trong thực tế, bao gồm:
Để hiểu rõ hơn về lý thuyết logarit, hãy cùng giải một số bài tập vận dụng:
Hy vọng với những kiến thức chi tiết và hữu ích trên đây, bạn đã có cái nhìn tổng quan về lý thuyết logarit trong SGK Toán 11. Chúc bạn học tập tốt và đạt kết quả cao!