Chào mừng bạn đến với chuyên mục Lý thuyết Đạo hàm - SGK Toán 11 của giaitoan.edu.vn. Đạo hàm là một trong những khái niệm quan trọng nhất trong chương trình Toán học, đặc biệt là ở bậc THPT. Việc nắm vững lý thuyết đạo hàm sẽ giúp bạn giải quyết các bài toán một cách nhanh chóng và chính xác.
Chúng tôi cung cấp các bài giảng chi tiết, dễ hiểu, cùng với các ví dụ minh họa sinh động, giúp bạn tiếp thu kiến thức một cách hiệu quả nhất.
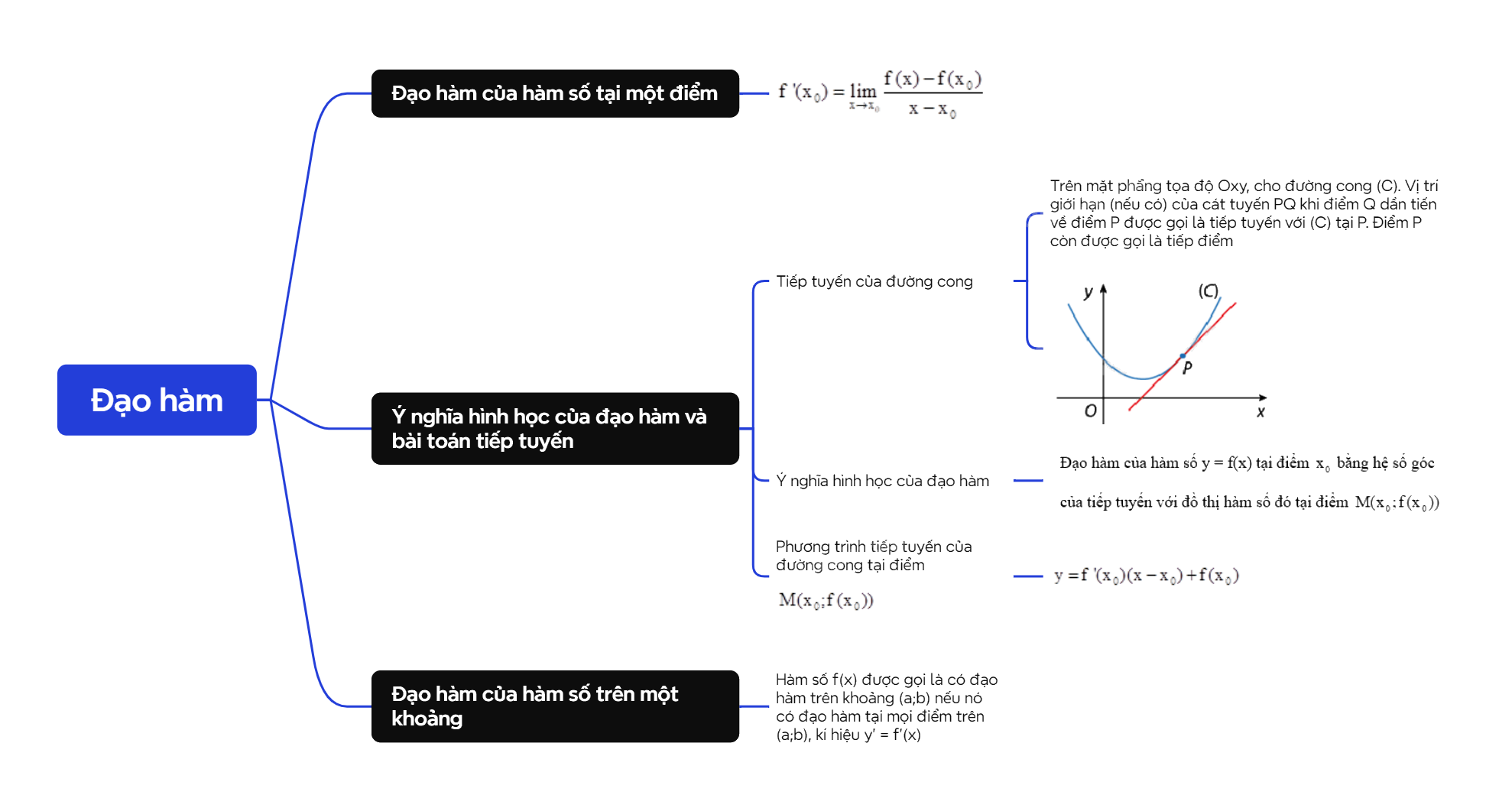
A. Lý thuyết 1. Đạo hàm của hàm số tại một điểm
A. Lý thuyết
1. Đạo hàm của hàm số tại một điểm
Cho hàm số y = f(x) xác định trên khoảng (a;b) và \({x_0} \in (a;b)\). Giới hạn hữu hạn (nếu có) \(\mathop {\lim }\limits_{x \to {x_0}} \frac{{f(x) - f({x_0})}}{{x - {x_0}}}\) được gọi là đạo hàm của hàm số y = f(x) tại điểm \({x_0}\), kí hiệu \(f'({x_0})\) hoặc \(y'({x_0})\), nghĩa là \(f'({x_0}) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f(x) - f({x_0})}}{{x - {x_0}}}\). |
Nhận xét:
- Nếu một chất điểm chuyển động thẳng với phương trình s = s(t) thì vận tốc tức thời của nó tại thời điểm \({t_0}\) bằng đạo hàm của hàm số s = s(t) tại \({t_0}\), tức là:
\(v({t_0}) = s'({t_0})\).
- Nếu nhiệt độ của một vật thay đổi theo thời gian bởi hàm số y = f(x) thì tốc độ thay đổi nhiệt độ của vật đó tại thời điểm \({t_0}\) bằng đạo hàm của hàm số y = f(x) tại \({t_0}\).
2. Ý nghĩa hình học của đạo hàm và bài toán tiếp tuyến
a) Tiếp tuyến của đường cong
Trên mặt phẳng tọa độ Oxy, cho đường cong (C). Vị trí giới hạn (nếu có) của cát tuyến PQ khi điểm Q dần tiến về điểm P được gọi là tiếp tuyến với (C) tại P. Điểm P còn được gọi là tiếp điểm.
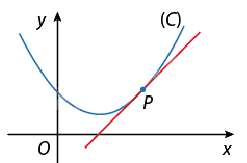
b) Ý nghĩa hình học của đạo hàm
Đạo hàm của hàm số y = f(x) tại điểm \({x_0}\) bằng hệ số góc của tiếp tuyến với đồ thị hàm số đó tại điểm \(M({x_0};f({x_0}))\).
c) Phương trình tiếp tuyến của đường cong
Cho hàm số y = f(x) có đồ thị (C). Nếu hàm số có đạo hàm tại điểm \({x_0}\) thì tiếp tuyến của (C) tại điểm \(M({x_0};f({x_0}))\) có phương trình là \(y = f'({x_0})(x - {x_0}) + f({x_0})\). |
3. Đạo hàm của hàm số trên một khoảng
| Hàm số f(x) được gọi là có đạo hàm trên khoảng (a;b) nếu nó có đạo hàm tại mọi điểm trên (a;b), kí hiệu y’ = f’(x). |
B. Bài tập
Bài 1: Tính đọa hàm của hàm số \(f(x) = {x^3}\) tại điểm \({x_0} = 1\).
Giải:
Ta có \(f'(1) = \mathop {\lim }\limits_{x \to 1} \frac{{f(x) - f(1)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{{x^3} - {1^3}}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{(x - 1)({x^2} + x + 1)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} ({x^2} + x + 1) = 3\).
Bài 2: Tìm hệ số góc của tiếp tuyến với đồ thị hàm số \(f(x) = 2{x^2}\) tại điểm có hoành độ \({x_0} = 1\). Viết phương trình tiếp tuyến đó.
Giải:
Ta có \(f'(1) = \mathop {\lim }\limits_{x \to 1} \frac{{f(x) - f(1)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{2{x^2} - 2}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{2(x + 1)(x - 1)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} 2(x + 1) = 4\).
Suy ra f’(1) = 4. Do đó hệ số góc của tiếp tuyến bằng 4.
Tiếp tuyến với đồ thị hàm số \(f(x) = 2{x^2}\) tại điểm có hoành độ \({x_0} = 1\) là:
\(f(x) = f'(1)(x - 1) + f(1)\) hay \(y = 4(x - 1) + 2\) hay \(y = 4x - 2\).
Bài 4: Tìm đạo hàm của hàm số \(y = {x^2} + x\) trên \(\mathbb{R}\).
Giải:
Với mọi \({x_0} \in \mathbb{R}\), ta có:
\(f'({x_0}) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f(x) - f({x_0})}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{{x^2} + x - {x_0}^2 + {x_0}}}{{x - {x_0}}}\)
\( = \mathop {\lim }\limits_{x \to {x_0}} \frac{{(x - {x_0})(x + {x_0}) + (x - {x_0})}}{{x - {x_0}}}\mathop {\lim }\limits_{x \to {x_0}} \frac{{x + {x_0} + 1}}{{x - {x_0}}} = 2{x_0} + 1\).
Đạo hàm của một hàm số tại một điểm là tốc độ thay đổi tức thời của hàm số đó tại điểm đó. Nó thể hiện độ dốc của tiếp tuyến với đồ thị hàm số tại điểm đó. Trong chương trình Toán 11, học sinh sẽ được làm quen với các khái niệm cơ bản về đạo hàm, các quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế.
Giả sử hàm số y = f(x) xác định trên khoảng (a; b). Nếu tồn tại giới hạn:
limΔx→0 [f(x + Δx) - f(x)] / Δx
thì hàm số f(x) được gọi là đạo hàm của hàm số tại x, ký hiệu là f'(x).
Để tính đạo hàm một cách nhanh chóng và hiệu quả, chúng ta cần nắm vững các quy tắc tính đạo hàm cơ bản:
Dưới đây là đạo hàm của một số hàm số cơ bản thường gặp:
| Hàm số | Đạo hàm |
|---|---|
| C (hằng số) | 0 |
| x | 1 |
| x2 | 2x |
| sin(x) | cos(x) |
| cos(x) | -sin(x) |
| ex | ex |
| ln(x) | 1/x |
Đạo hàm có rất nhiều ứng dụng trong toán học và các lĩnh vực khác:
Để củng cố kiến thức về lý thuyết đạo hàm, bạn có thể thực hành giải các bài tập sau:
Lý thuyết Đạo hàm là một phần quan trọng của chương trình Toán 11. Việc nắm vững lý thuyết và các quy tắc tính đạo hàm sẽ giúp bạn giải quyết các bài toán một cách hiệu quả và tự tin hơn. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.