Chào mừng bạn đến với bài học về Lý thuyết Phương trình và bất phương trình logarit, một phần quan trọng trong chương trình Toán 11. Tại giaitoan.edu.vn, chúng tôi cung cấp tài liệu học tập đầy đủ, dễ hiểu, giúp bạn nắm vững kiến thức nền tảng và tự tin giải quyết các bài tập.
Bài học này sẽ tập trung vào các khái niệm cơ bản về logarit, các tính chất của logarit, phương pháp giải phương trình và bất phương trình logarit, cùng với các ví dụ minh họa cụ thể.
1. Phương trình logarit cơ bản Phương trình mũ cơ bản có
A. Lý thuyết
1. Phương trình logarit cơ bản
Phương trình mũ cơ bản có dạng \({\log _a}x = b\) \((a > 0,a \ne 1)\).
| Phương trình \({\log _a}x = b\) \((a > 0,a \ne 1)\) luôn có nghiệm duy nhất \(x = {a^b}\) với mọi b. |
Lưu ý: Nếu \(b = {\log _a}\alpha \) \((\alpha > 0)\) thì phương trình \({\log _a}x = b\) trở thành \({\log _a}x = {\log _a}\alpha \) với mọi b. Khi đó, phương trình có nghiệm duy nhất \(x = \alpha \). Một cách tổng quát, với a > 0 và \(a \ne 1\) , ta có:
\({\log _a}A = {\log _a}B \Leftrightarrow \left\{ \begin{array}{l}A > 0\\B > 0\\A = B\end{array} \right.\).
2. Bất phương trình logarit cơ bản
Bất phương trình mũ cơ bản có dạng \({\log _a}x > b\) hoặc \({\log _a}x \ge b\), \({\log _a}x < b\), \({\log _a}x \le b\) \((a > 0,a \ne 1)\).
Cho bất phương trình \({\log _a}x > b\) \((a > 0,a \ne 1)\): - Nếu a > 1: Ta có \({\log _a}x > b \Leftrightarrow x > {a^b}\). - Nếu 0 < a < 1: Ta có \({\log _a}x > b \Leftrightarrow 0 < x < {a^b}\). |
Lưu ý:
Giải tương tự cho các trường hợp còn lại: \({\log _a}x \ge b\), \({\log _a}x < b\), \({\log _a}x \le b\).
Nếu \(b = {\log _a}\alpha \) \((\alpha > 0)\) thì bất phương trình \({\log _a}x > b\) trở thành \({\log _a}x > {\log _a}\alpha \). Khi đó:
- Nếu a > 1 thì \({\log _a}x > {\log _a}\alpha \Leftrightarrow x > \alpha \).
- Nếu 0 < a < 1 thì \({\log _a}x > {\log _a}\alpha \Leftrightarrow x < \alpha \).
Một cách tổng quát, ta có:
- Khi a > 1 thì \({\log _a}A > {\log _a}B \Leftrightarrow A > B > 0\).
- Khi 0 < a < 1 thì \({\log _a}A > {\log _a}B \Leftrightarrow 0 < A < B\).
B. Bài tập
Bài 1: Giải các phương trình:
a) \({\log _2}(x + 1) = 3\).
b) \(\ln (x + 1) = ln({x^2} - 1)\).
Giải:
a) Điều kiện của phương trình là \(x + 1 > 0 \Leftrightarrow x > - 1\).
Ta có \({\log _2}(x + 1) = 3 \Leftrightarrow x + 1 = {2^3} \Leftrightarrow x + 1 = 8 \Leftrightarrow x = 7\).
Vậy phương trình có nghiệm duy nhất x = 7.
b) Điều kiện của phương trình là \(\left\{ \begin{array}{l}x + 1 > 0\\{x^2} - 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > - 1\\\left[ \begin{array}{l}x < - 1\\x > 1\end{array} \right.\end{array} \right. \Leftrightarrow x > 1\).
Ta có \(\ln (x + 1) = ln({x^2} - 1) \Rightarrow x + 1 = {x^2} - 1\).
\(x + 1 = {x^2} - 1 \Leftrightarrow {x^2} - x - 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 2\end{array} \right.\).
Kết hợp với điều kiện của phương trình, ta loại x = -1 và nhận x = 2.
Vậy phương trình có nghiệm duy nhất x = 2.
Bài 2: Giải các bất phương trình:
a) \({\log _2}x > 7\).
b) \({\log _{0,5}}(6x + 12) < {\log _{0,5}}({x^2} + 7x + 10)\).
Giải:
a) Vì cơ số 2 lớn hơn 1 nên \({\log _2}x > 7 \Leftrightarrow x > {2^7} \Leftrightarrow x > 128\).
Vậy tập nghiệm của bất phương trình là \((128; + \infty )\).
b) Điều kiện của bất phương trình là \(\left\{ \begin{array}{l}6x + 12 > 0\\{x^2} + 7x + 10 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > - 2\\\left[ \begin{array}{l}x < - 5\\x > - 2\end{array} \right.\end{array} \right. \Leftrightarrow x > - 2\).
Vì cơ số 0,5 nhỏ hơn 1 nên \({\log _{0,5}}(6x + 12) < {\log _{0,5}}({x^2} + 7x + 10) \Leftrightarrow 6x + 12 > {x^2} + 7x + 10 \Leftrightarrow {x^2} + x - 2 < 0 \Leftrightarrow - 2 < x < 1\).
Kết hợp điều kiện, ta được tập nghiệm của bất phương trình là \(( - 2;1)\).
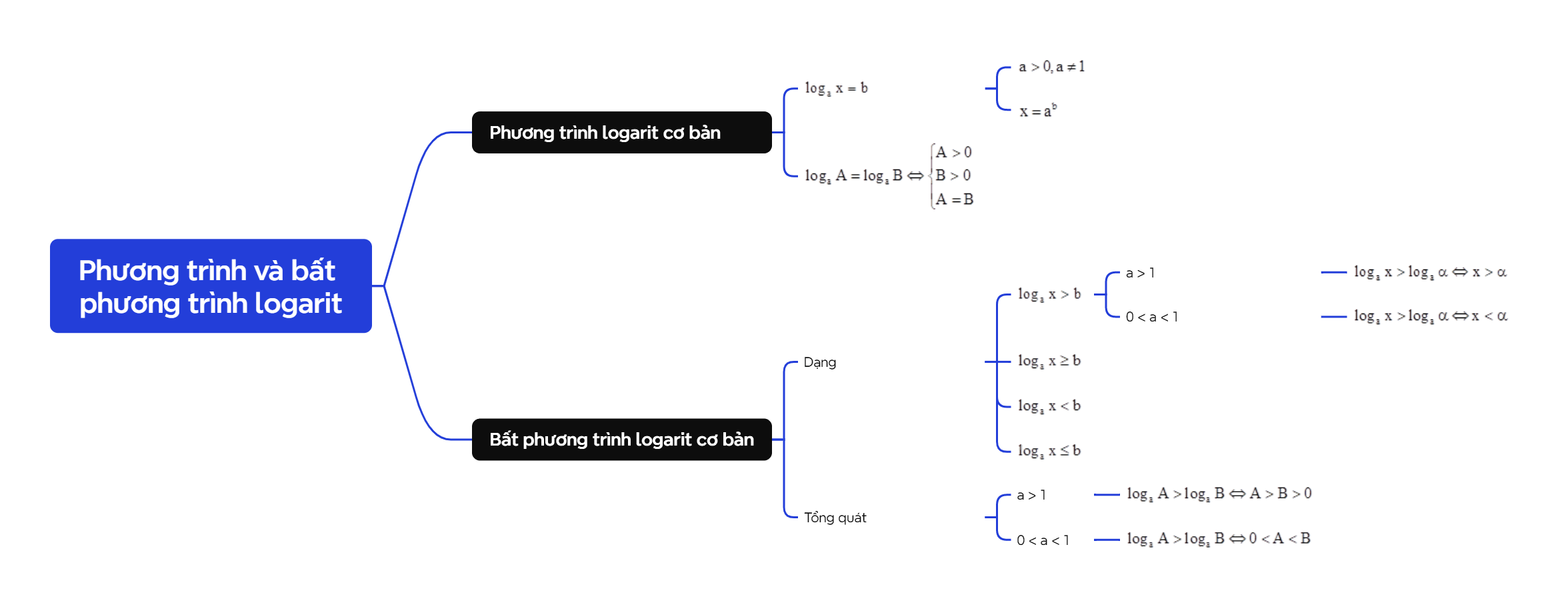
Logarit là một khái niệm quan trọng trong toán học, đặc biệt là trong việc giải quyết các bài toán liên quan đến hàm mũ. Hiểu rõ lý thuyết logarit là nền tảng để giải quyết các phương trình và bất phương trình logarit một cách hiệu quả.
Logarit của một số dương b theo cơ số a (với a > 0 và a ≠ 1) là số x sao cho ax = b. Ký hiệu: logab = x.
Phương trình logarit là phương trình có chứa ẩn số trong biểu thức logarit. Để giải phương trình logarit, ta thường sử dụng các tính chất của logarit để đưa phương trình về dạng đơn giản hơn, sau đó giải phương trình tương đương.
Ví dụ: Giải phương trình log2(x + 1) = 3
Ta có: x + 1 = 23 => x + 1 = 8 => x = 7
Bất phương trình logarit là bất phương trình có chứa ẩn số trong biểu thức logarit. Khi giải bất phương trình logarit, cần chú ý đến điều kiện xác định của logarit và chiều của bất đẳng thức khi đổi cơ số hoặc sử dụng các tính chất của logarit.
Ví dụ: Giải bất phương trình log1/2(x - 2) > 1
Điều kiện: x - 2 > 0 => x > 2
Ta có: x - 2 < (1/2)1 => x - 2 < 1/2 => x < 5/2
Kết hợp điều kiện, ta có: 2 < x < 5/2
Để nắm vững kiến thức về Lý thuyết Phương trình và bất phương trình logarit, bạn nên luyện tập thường xuyên với các bài tập khác nhau. Tại giaitoan.edu.vn, chúng tôi cung cấp một hệ thống bài tập phong phú, đa dạng, được phân loại theo mức độ khó, giúp bạn củng cố kiến thức và rèn luyện kỹ năng giải toán.
Lý thuyết Phương trình và bất phương trình logarit là một phần quan trọng trong chương trình Toán 11. Việc nắm vững kiến thức này không chỉ giúp bạn giải quyết các bài toán trong sách giáo khoa mà còn là nền tảng cho các kiến thức toán học nâng cao hơn. Hãy dành thời gian học tập và luyện tập để đạt kết quả tốt nhất!
| Công thức | Mô tả |
|---|---|
| loga(xy) = logax + logay | Logarit của tích bằng tổng các logarit |
| loga(x/y) = logax - logay | Logarit của thương bằng hiệu các logarit |