Chào mừng các em học sinh đến với bài giải chi tiết mục 2 trang 22, 23 SGK Toán 11 tập 2 tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải đầy đủ, dễ hiểu, giúp các em hiểu rõ bản chất của bài toán và rèn luyện kỹ năng giải toán.
Mục tiêu của chúng tôi là hỗ trợ các em học tập hiệu quả, đạt kết quả cao trong môn Toán.
Ta biết: Với (C1) là đồ thị của hàm số y = f(x) và (C2) là đồ thị của hàm số y = g(x)
Ta biết: Với (C1) là đồ thị của hàm số y = f(x) và (C2) là đồ thị của hàm số y = g(x) thì tập hợp giá trị của x để (C1) nằm phía trên (C2) là tập nghiệm của bất phương trình f(x) > g(x).
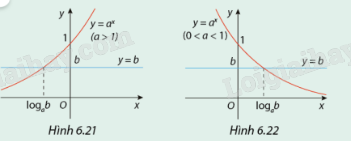
Quan sát các đồ thị (Hình 6.21 và 6.22) trong Hoạt động 1 và trong mỗi trường hợp, hãy tìm các tập nghiệm của bất phương trình ax > b:
a) Khi b > 0;
b) Khi b ≤ 0.
Phương pháp giải:
Quan sát hình vẽ.
Lời giải chi tiết:
a) Khi b > 0:
a > 1: ax > b \( \Leftrightarrow x > {\log _a}b\)
0 < a < 1: ax > b \( \Leftrightarrow x < {\log _a}b\)
b) Khi b ≤ 0 thì bất phương trình nghiệm đúng với mọi \(x \in \mathbb{R}\).
Giải các bất phương trình sau:
a) \({2^{x + 1}} > {2^{3x + 5}}\)
b) \({\left( {\frac{7}{9}} \right)^{2{x^2} - 3x}} \le \frac{9}{7}\)
Phương pháp giải:
Khi a > 1: \({a^{A\left( x \right)}} > {a^{B\left( x \right)}} \Leftrightarrow A\left( x \right) > B\left( x \right)\)
Khi 0 < a < 1: \({a^{A\left( x \right)}} > {a^{B\left( x \right)}} \Leftrightarrow A\left( x \right) < B\left( x \right)\)
Lời giải chi tiết:
a)
\(\begin{array}{l}{2^{x + 1}} > {2^{3x + 5}}\\ \Leftrightarrow x + 1 > 3x + 5\\ \Leftrightarrow - 2x > 4\\ \Leftrightarrow x < - 2\end{array}\)
Vậy tập nghiệm của bất phương trình đã cho là \(\left( { - \infty ; - 2} \right)\).
b)
\(\begin{array}{l}{\left( {\frac{7}{9}} \right)^{2{x^2} - 3x}} \le \frac{9}{7}\\ \Leftrightarrow {\left( {\frac{7}{9}} \right)^{2{x^2} - 3x}} \le {\left( {\frac{7}{9}} \right)^{ - 1}}\\ \Leftrightarrow 2{x^2} - 3x \ge - 1\\ \Leftrightarrow 2{x^2} - 3x + 1 \ge 0\\ \Leftrightarrow \left[ \begin{array}{l}x \ge 1\\x \le \frac{1}{2}\end{array} \right.\end{array}\)
Vậy tập nghiệm của bất phương trình đã cho là \(\left( { - \infty ;\frac{1}{2}} \right) \cup \left( {1; + \infty } \right)\).
Mục 2 của SGK Toán 11 tập 2 thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này, học sinh cần nắm vững kiến thức lý thuyết, các định nghĩa, định lý và công thức liên quan. Việc hiểu rõ bản chất của vấn đề là yếu tố then chốt để tìm ra phương pháp giải phù hợp.
Tùy thuộc vào chương trình học, mục 2 trang 22, 23 có thể bao gồm các nội dung sau:
Dưới đây là hướng dẫn giải chi tiết một số bài tập tiêu biểu trong mục 2 trang 22, 23 SGK Toán 11 tập 2. Lưu ý rằng, các bài tập có thể khác nhau tùy thuộc vào chương trình học và phiên bản SGK.
Đề bài: (Giả định một bài tập cụ thể về hàm số, giới hạn, đạo hàm, tích phân, hoặc hình học tùy thuộc vào chương trình học)
Lời giải:
Đề bài: (Giả định một bài tập cụ thể khác)
Lời giải: (Tương tự như bài tập 1)
Để giải các bài tập Toán 11 tập 2 một cách hiệu quả, các em có thể tham khảo một số mẹo sau:
Kiến thức trong mục 2 trang 22, 23 SGK Toán 11 tập 2 có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, như:
Hy vọng rằng, với hướng dẫn chi tiết và các mẹo giải toán hiệu quả trên đây, các em học sinh sẽ tự tin giải quyết các bài tập trong mục 2 trang 22, 23 SGK Toán 11 tập 2. Chúc các em học tập tốt và đạt kết quả cao!