Chào mừng bạn đến với bài học về lý thuyết các tứ phân vị của mẫu số liệu ghép nhóm trong chương trình Toán 11. Bài học này sẽ cung cấp cho bạn kiến thức nền tảng về các tứ phân vị, cách tính toán và ứng dụng của chúng trong thống kê.
Tại giaitoan.edu.vn, chúng tôi cam kết mang đến cho bạn những bài giảng chất lượng, dễ hiểu và phù hợp với chương trình SGK Toán 11.
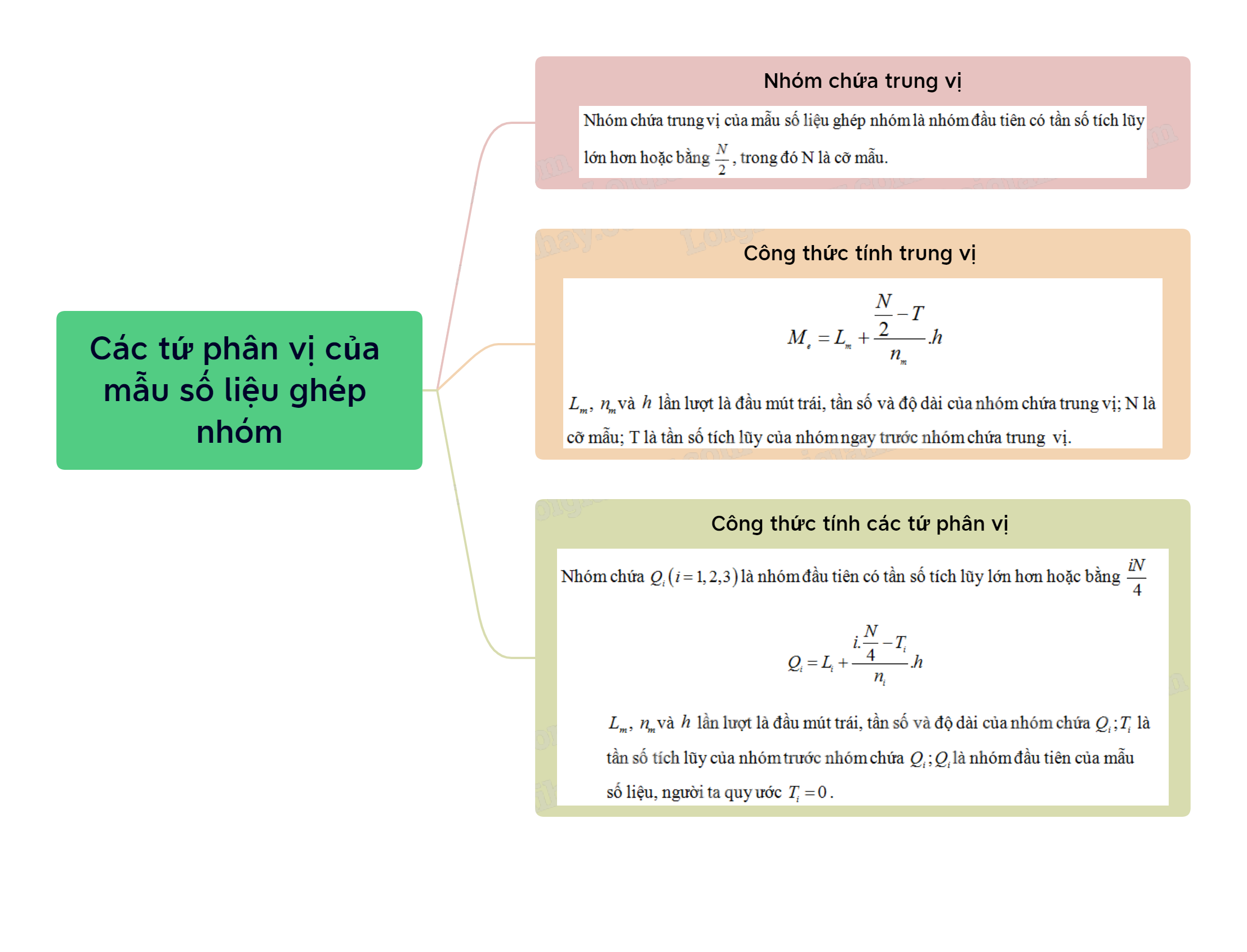
I. Nhóm chứa trung vị
I. Nhóm chứa trung vị
Nhóm chứa trung vị của mẫu số liệu ghép nhóm là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{N}{2}\), trong đó N là cỡ mẫu.
II. công thức tính trung vị của mẫu số liệu ghép nhóm
\({M_e} = {L_m} + \frac{{\frac{N}{2} - T}}{{{n_m}}}.h\)
Trong đó:
* Ý nghĩa: Trung vị của mẫu số liệu ghép nhóm là giá trị xấp xỉ cho trung vị của mẫu số liệu và có thể sử dụng làm giá trị đại diện cho mẫu số liệu.
III. Công thức tính các tứ phân vị của mẫu số liệu ghép nhóm
Công thức tính các tứ phân vị \({Q_1},{Q_2},{Q_3}\) của mẫu số liệu ghép nhóm:
Nhóm chứa \({Q_i}\left( {i = 1,2,3} \right)\) là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{{iN}}{4}\) và
\({Q_i} = {L_i} + \frac{{i.\frac{N}{4} - {T_i}}}{{{n_i}}}.h\)
Trong đó:
* Lưu ý: Trong trường hợp các nhóm có độ dài bằng nhau thì h giống nhau với mọi nhóm.
* Ý nghĩa:
- Tứ phân vị của mẫu số liệu ghép nhóm là giá trị xấp xỉ của tứ phân vị của mẫu số liệu.
- Các tứ phân vị \({Q_1},{Q_2},{Q_3}\) chia mẫu số liệu ghép nhóm thành 4 phần có số liệu bằng nhau. Các tứ phân vị cho ta một hình ảnh về sự phân bố của mẫu số liệu. Dựa vào các tứ phân vị, ta có thể biết số liệu tập trung ít hay nhiều quanh trung vị.
Trong thống kê, các tứ phân vị là những giá trị chia một tập dữ liệu đã được sắp xếp thành bốn phần bằng nhau. Việc hiểu rõ về các tứ phân vị giúp chúng ta đánh giá sự phân bố của dữ liệu và xác định các giá trị đặc trưng của nó.
Giả sử ta có một mẫu số liệu đã được sắp xếp theo thứ tự không giảm: x1 ≤ x2 ≤ ... ≤ xn.
Khi làm việc với mẫu số liệu ghép nhóm, việc tính toán tứ phân vị trở nên phức tạp hơn. Dưới đây là các bước thực hiện:
Qi = bk + [(Vị trí Qi - Fk-1)/fk] * h
Trong đó:Các tứ phân vị cung cấp thông tin quan trọng về sự phân bố của dữ liệu:
Khoảng tứ phân vị (IQR) được tính bằng hiệu của Q3 và Q1: IQR = Q3 - Q1. Khoảng tứ phân vị cho biết mức độ phân tán của 50% dữ liệu trung tâm.
Giả sử ta có bảng tần số sau:
| Khoảng lớp | Tần số (f) | Tần số tích lũy (F) |
|---|---|---|
| [10-20) | 5 | 5 |
| [20-30) | 10 | 15 |
| [30-40) | 15 | 30 |
| [40-50) | 8 | 38 |
| [50-60) | 2 | 40 |
Tổng số quan sát (n) = 40.
Vị trí Q1 = 40/4 = 10. Khoảng lớp chứa Q1 là [20-30). Q1 = 20 + [(10-5)/10] * 10 = 25.
Vị trí Q2 = 40/2 = 20. Khoảng lớp chứa Q2 là [30-40). Q2 = 30 + [(20-15)/15] * 10 = 33.33.
Vị trí Q3 = (3*40)/4 = 30. Khoảng lớp chứa Q3 là [30-40). Q3 = 30 + [(30-15)/15] * 10 = 40.
Các tứ phân vị được sử dụng rộng rãi trong nhiều lĩnh vực, bao gồm:
Hy vọng bài học này đã giúp bạn hiểu rõ hơn về lý thuyết các tứ phân vị của mẫu số liệu ghép nhóm. Hãy luyện tập thêm với các bài tập để nắm vững kiến thức này nhé!