Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 2 trang 67, 68, 69 của sách giáo khoa Toán 11 tập 1.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài toán, nắm vững phương pháp giải và tự tin làm bài tập.
Cho hàm số (f(x) = left{ begin{array}{l}x + 2,x ge 1\x - 4,x < 1end{array} right.) và hai dãy số (({u_n})) và (({v_n})) với ({u_n} = 1 + frac{1}{n}), ({v_n} = 1 - frac{1}{n})
Cho hàm số \(f(x) = \left\{ \begin{array}{l}x + 2,x \ge 1\\x - 4,x < 1\end{array} \right.\) và hai dãy số (\({u_n}\)) và (\({v_n}\)) với \({u_n} = 1 + \frac{1}{n}\), \({v_n} = 1 - \frac{1}{n}\)
a, So sánh \({u_n},{v_n}\) với 1 và tìm \(\lim {u_n}\), \(\lim {v_n}\).
b, Tính \(f({u_n})\) và \(f({v_n})\) theo n.
c, Tìm lim\(f({u_n})\) và lim\(f({v_n})\).
Phương pháp giải:
a, Xác định \(\lim \frac{1}{n}\) để so sánh \({u_n},{v_n}\) với 1 và tìm \(\lim {u_n}\), \(\lim {v_n}\).
b, Thay \({u_n} = 1 + \frac{1}{n}\), \({v_n} = 1 - \frac{1}{n}\) để tính \(f({u_n})\) và \(f({v_n})\).
c, Sử dụng câu a,b để tìm lim\(f({u_n})\) và lim\(f({v_n})\).
Lời giải chi tiết:
a, Ta có \(\lim \frac{1}{n} = 0\) và \(\frac{1}{n} > 0\) nên:
\({u_n} = 1 + \frac{1}{n} > 1\) và \({v_n} = 1 - \frac{1}{n} < 1\)
\(\lim {u_n} = \lim (1 + \frac{1}{n}) = 1\) và \(\lim {v_n} = \lim (1 - \frac{1}{n}) = 1\).
b, Với \({u_n} > 1\) thay x=\({u_n}\) vào f(x)=x+2 ta được:
\(f({u_n}) = {u_n} + 2 = 1 + \frac{1}{n} + 2 = 3 + \frac{1}{n}\).
Với \({v_n} < 1\) thay x=\({v_n}\) vào f(x) = x-4 ta được:
\(f({v_n}) = {v_n} - 4 = 1 - \frac{1}{n} - 4 = - 3 - \frac{1}{n}\).
c, Ta có: \(\lim f({u_n}) = \lim (3 + \frac{1}{n}) = 3\).
\(\lim f({v_n}) = \lim ( - 3 - \frac{1}{n}) = - 3\).
Cho hàm số \(f(x) = \left\{ \begin{array}{l}{x^2} + 1,x \ge 1\\\frac{{{x^2} - 1}}{{x + 1}},x < 1\end{array} \right.\). Tính \(\mathop {\lim }\limits_{x \to {1^ + }} f(x)\)và \(\mathop {\lim }\limits_{x \to {1^ - }} f(x)\)
Phương pháp giải:
\(\mathop {\lim }\limits_{x \to - {1^ + }} f(x) = \lim ({x_n}^2 + 1)\)
\(\mathop {\lim }\limits_{x \to - {1^ - }} f(x) = \lim \frac{{{x_n}^2 - 1}}{{{x_n} + 1}}\)
Lời giải chi tiết:
Giả sử \(({x_n})\) là một dãy số bất kì mà \({x_n} > - 1\) và \(\lim {x_n} = - 1\), ta có \(f\left( {{x_n}} \right) = x_n^2 + 1\).
Vậy\(\mathop {\lim }\limits_{x \to - {1^ + }} f(x)\) =\(\lim f({x_n}) = {( - 1)^2} + 1 = 2\).
Giả sử \(({x_n})\) là một dãy số bất kì mà \({x_n} < - 1\) và \(\lim {x_n} = - 1\), ta có \(f({x_n}) = \frac{{x_n^2 - 1}}{{{x_n} + 1}} = \frac{{({x_n} - 1)({x_n} + 1)}}{{{x_n} + 1}} = {x_n} - 1\)
Vậy \(\mathop {\lim }\limits_{x \to - {1^ - }} f(x) = \)\(\lim f({x_n}) = - 1 - 1 = - 2\).
Cho hàm số \(f(x) = \left\{ \begin{array}{l}2ax + 6,x \ge - 2\\\frac{{{x^2} - 4}}{{x + 2}},x < - 2\end{array} \right.\). Tìm a, biết rằng tồn tại \(\mathop {\lim }\limits_{x \to - 2} f(x)\)
Phương pháp giải:
\(\mathop {\lim }\limits_{x \to - {2^ + }} f(x) = \mathop {\lim }\limits_{x \to - {2^ + }} (2ax + 6) = - 4a + 6\)
\(\mathop {\lim }\limits_{x \to - {2^ - }} f(x) = \mathop {\lim }\limits_{x \to - {2^ - }} \frac{{{x^2} - 4}}{{x + 2}}\mathop { = \lim }\limits_{x \to - {2^ - }} (x - 2) = - 4\)
Cho \(\mathop {\lim }\limits_{x \to - {2^ + }} f(x) = \mathop {\lim }\limits_{x \to - {2^ - }} f(x)\) để tìm giá trị của a.
Lời giải chi tiết:
Ta có: \(\mathop {\lim }\limits_{x \to - {2^ + }} f(x) = \mathop {\lim }\limits_{x \to - {2^ + }} (2ax + 6) = - 4a + 6\)
\(\mathop {\lim }\limits_{x \to - {2^ - }} f(x) = \mathop {\lim }\limits_{x \to - {2^ - }} \frac{{{x^2} - 4}}{{x + 2}}\mathop { = \lim }\limits_{x \to - {2^ - }} (x - 2) = - 4\)
Để tồn tại \(\mathop {\lim }\limits_{x \to - 2} f(x)\) thì \(\mathop {\lim }\limits_{x \to - {2^ + }} f(x) = \mathop {\lim }\limits_{x \to - {2^ - }} f(x) \Leftrightarrow - 4a + 6 = - 4 \Leftrightarrow - 4a = - 10 \Leftrightarrow a = \frac{5}{2}\)
Vậy \(a = \frac{5}{2}\).
Đồ thị hàm số \(y = f(x) = \frac{1}{{x - 2}}\) được cho trong hình 3.3
a, Nếu M(x;f(x)) là một điểm trên đồ thị, hãy dự đoán giá trị của f(x) khi x dần đến 2 theo phía phải, theo phía trái.
b, \(({x_n})\)là một dãy số bất kì mà \({x_n} < 2\) và \({\mathop{\rm l}\nolimits} {\rm{im }}{{\rm{x}}_n} = 2\).Tính \(f({x_n})\) và \(\lim f({x_n})\).
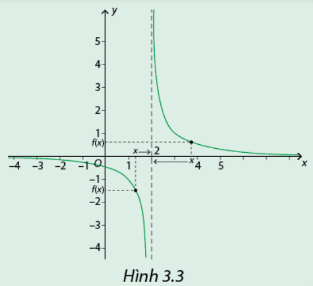
Phương pháp giải:
a, Dựa vào phần đồ thị bên phải để xác định giá trị của f(x) khi x gần đến 2 theo phía phải và phần đồ thị bên trái để xác định giá trị của f(x) khi x gần đến 2 theo phía trái.
b, Thay \(x = {x_n}\) để tính \(f({x_n})\).
Tìm \(\mathop {\lim }\limits_{x \to {2^ - }} f(x)\) và \(\mathop {\lim }\limits_{x \to {2^ + }} f(x)\).
Lời giải chi tiết:
a, Dự đoán: Khi x gần đến 2 theo phía phải thì f(x) gần đến \( + \infty \)
Khi x gần đến 2 theo phía trái thì f(x) gần đến \( - \infty \).
b, Thay \(x = {x_n}\) vào f(x) ta được : \(f({x_n}) = \frac{1}{{{x_n} - 2}}\)
Cho dãy số \(({x_n})\) với \({x_n} > 2\) và \({\mathop{\rm l}\nolimits} {\rm{im }}{{\rm{x}}_n} = 2\), lim1=1 ta có:
\(\lim f({x_n}) = + \infty \)
Cho dãy số \(({x_n})\) với \({x_n} < 2\) và \({\mathop{\rm l}\nolimits} {\rm{im }}{{\rm{x}}_n} = 2\), lim 1=1 ta có:
\(\lim f({x_n}) = - \infty \).
Tìm \(\mathop {\lim }\limits_{x \to {2^ - }} \frac{1}{{2 - x}}\) và \(\mathop {\lim }\limits_{x \to {4^ + }} \frac{1}{{x - 4}}\).
Phương pháp giải:
Áp dụng định lí \(\mathop {\lim }\limits_{x \to {a^ + }} \frac{1}{{x - a}} = + \infty \) và \(\mathop {\lim }\limits_{x \to {a^ - }} \frac{1}{{x - a}} = - \infty \) với mọi số thực a.
Lời giải chi tiết:
Ta có: \(\mathop {\lim }\limits_{x \to {2^ - }} \frac{1}{{2 - x}} = \mathop {\lim }\limits_{x \to {2^ - }} \frac{{ - 1}}{{x - 2}} = + \infty \)
\(\mathop {\lim }\limits_{x \to {4^ + }} \frac{1}{{x - 4}} = + \infty \)
Mục 2 của SGK Toán 11 tập 1 thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững kiến thức lý thuyết, các định nghĩa, định lý và công thức liên quan. Việc hiểu rõ bản chất của vấn đề cũng rất quan trọng để lựa chọn phương pháp giải phù hợp.
Bài tập này thường yêu cầu học sinh vận dụng kiến thức về... (giả sử bài tập 1 liên quan đến giới hạn). Để giải bài tập này, ta cần:
Ví dụ minh họa: ... (giải chi tiết bài tập 1)
Bài tập này có thể liên quan đến... (giả sử bài tập 2 liên quan đến đạo hàm). Để giải quyết bài tập này, ta cần:
Ví dụ minh họa: ... (giải chi tiết bài tập 2)
Bài tập này thường là một bài toán tổng hợp, yêu cầu học sinh vận dụng kiến thức từ nhiều phần khác nhau của chương. Để giải bài tập này, ta cần:
Ví dụ minh họa: ... (giải chi tiết bài tập 3)
Trong quá trình giải các bài tập Toán 11 tập 1, học sinh có thể gặp phải nhiều phương pháp khác nhau. Một số phương pháp thường gặp bao gồm:
Để đạt được kết quả tốt nhất khi giải bài tập Toán 11 tập 1, học sinh cần lưu ý một số điều sau:
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức và kỹ năng giải bài tập:
Hy vọng rằng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh đã có thể tự tin giải quyết các bài tập trong mục 2 trang 67, 68, 69 SGK Toán 11 tập 1. Chúc các em học tập tốt!