Chào mừng các em học sinh đến với bài giải chi tiết mục 1 trang 142 SGK Toán 11 tập 1 trên giaitoan.edu.vn. Chúng tôi cung cấp lời giải đầy đủ, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Bài học này thuộc chương trình Toán 11 tập 1, tập trung vào các kiến thức cơ bản về phép biến hình.
Bảng 5.27 phân loại cân nặng của một số học sinh. Nhóm nào chứa nhiều số liệu nhất?
Bảng 5.27 phân loại cân nặng của một số học sinh. Nhóm nào chứa nhiều số liệu nhất?
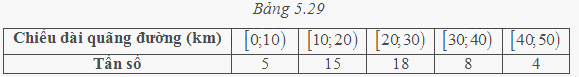
Phương pháp giải:
Tần số nào lớn nhất là nhóm đó chứa nhiều số liệu nhất
Lời giải chi tiết:
Quan sát dòng tấn số trong bảng, ta thấy 25 là số lớn nhất. Nhóm có tần số này là \(\left[ {50;55} \right)\). Vậy nhóm chứa nhiều số liệu nhất là nhóm \(\left[ {50;55} \right)\)
Bảng 5.29 do người chủ một cơ sở cho thuê xe đạp lập nên sau khi điều tra 50 khách thuê xe trong hai ngày cuối tuần về chiều dài quãng đường mà mỗi người đã thực hiện. Hãy chỉ ra nhóm chứa mốt của mẫu số liệu.
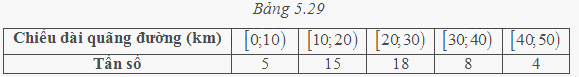
Phương pháp giải:
Nhóm có tần số lớn nhất được gọi là nhóm chứa mốt.
Lời giải chi tiết:
Quan sát dòng tấn số trong bảng, ta thấy 18 là số lớn nhất. Nhóm có tần số này là . Vậy nhóm chứa mốt là nhóm . Nó cho ta biết khoảng chiều dài quãng đường do chủ một cơ sở cho thuê xe đạp lập nên, chiều dài quãng đường từ 20 km đến dưới 30 km chiếm số lượng nhiều nhất.
Mục 1 trang 142 SGK Toán 11 tập 1 giới thiệu về phép biến hình, một khái niệm quan trọng trong hình học. Phép biến hình là một ứng dụng biến mỗi điểm của mặt phẳng thành một điểm khác, tuân theo một quy tắc nhất định. Việc hiểu rõ về phép biến hình là nền tảng để giải quyết các bài toán liên quan đến đối xứng, tịnh tiến, quay và các phép biến hình khác.
Dưới đây là giải chi tiết các bài tập trong mục 1 trang 142 SGK Toán 11 tập 1:
Bài tập này yêu cầu học sinh xác định loại phép biến hình dựa trên các thông tin đã cho. Ví dụ, cho một điểm A và ảnh A' sau khi thực hiện một phép biến hình, học sinh cần xác định đó là phép tịnh tiến, phép quay hay phép đối xứng.
Lời giải: Để giải bài tập này, học sinh cần nắm vững định nghĩa và tính chất của từng loại phép biến hình. Phân tích vị trí tương đối của điểm A và A' để xác định quy tắc biến hình.
Bài tập này yêu cầu học sinh thực hiện một phép biến hình cụ thể trên một đối tượng hình học. Ví dụ, tịnh tiến một đường thẳng theo một vector cho trước.
Lời giải: Sử dụng công thức biến hình tương ứng với từng loại phép biến hình. Ví dụ, để tịnh tiến một điểm M(x, y) theo vector v = (a, b), ta có M'(x + a, y + b).
Bài tập này yêu cầu học sinh chứng minh một tính chất nào đó của phép biến hình. Ví dụ, chứng minh rằng phép tịnh tiến bảo toàn khoảng cách giữa hai điểm.
Lời giải: Sử dụng định nghĩa và tính chất của phép biến hình, kết hợp với các kiến thức hình học đã học để chứng minh.
Phép biến hình có nhiều ứng dụng trong thực tế, bao gồm:
Hy vọng bài giải chi tiết mục 1 trang 142 SGK Toán 11 tập 1 trên giaitoan.edu.vn sẽ giúp các em học sinh hiểu rõ hơn về phép biến hình và tự tin giải các bài tập liên quan. Chúc các em học tập tốt!