Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau khám phá và giải chi tiết các bài tập trong mục 3 trang 5 và 6 của sách giáo khoa Toán 11 tập 2.
Mục tiêu của chúng tôi là cung cấp cho các em những lời giải chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Ở lớp dưới, ta đã biết số (sqrt 2 ) là một số vô tỉ được biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn
Ở lớp dưới, ta đã biết số \(\sqrt 2 \) là một số vô tỉ được biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn: \(\sqrt 2 \) = 1,414213562... Gọi \({r_n}\) là số hữu tỉ được tạo thành từ n chữ số đầu tiên dùng để viết \(\sqrt 2 \) ở dạng thập phân, n = 1, 2,..., 10,...
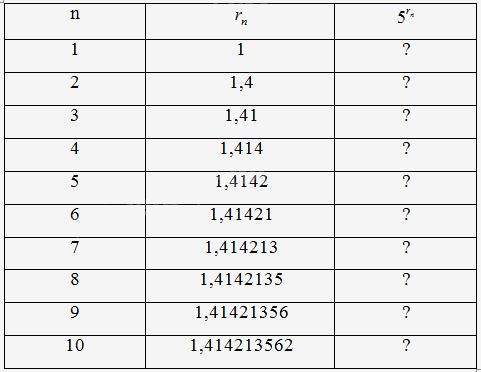
a) Sử dụng máy tính cầm tay, hãy tìm các số \({5^{{r_n}}}\) tương ứng (với 9 chữ số thập phân) cho mỗi dấu "?" trong bảng bên phải. Người ta chứng minh được rằng khi \(n \to + \infty \) thì dãy số (\({5^{{r_n}}}\)) dần đến một giới hạn mà ta kí hiệu là \({5^{\sqrt 2 }}\).
b) Sử dụng máy tính cầm tay, tính \({5^{\sqrt 2 }}\) (với 9 chữ số thập phân).
Phương pháp giải:
Sử dụng máy tính cầm tay.
Lời giải chi tiết:
a,
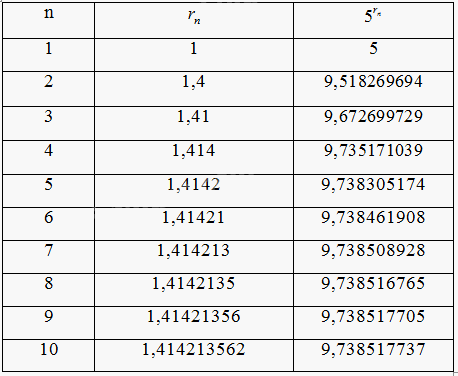
b) \({5^{\sqrt 2 }} \approx 9,738517742\)
Rút gọn biểu thức \(\frac{{{{\left( {{a^{\sqrt 3 - 1}}} \right)}^{\sqrt 3 + 1}}}}{{{a^{\sqrt 5 - 3}}.{a^{4 - \sqrt 5 }}}}\,\,\left( {a > 0} \right)\).
Phương pháp giải:
Áp dụng: \({\left( {{a^n}} \right)^m} = {a^{n.m}};\,{a^n}.{a^m} = {a^{n + m}}\)
Lời giải chi tiết:
Ta có: \(\frac{{{{\left( {{a^{\sqrt 3 - 1}}} \right)}^{\sqrt 3 + 1}}}}{{{a^{\sqrt 5 - 3}}.{a^{4 - \sqrt 5 }}}} = \frac{{{a^{\left( {\sqrt 3 - 1} \right)\left( {\sqrt 3 + 1} \right)}}}}{{{a^{\sqrt 5 - 3 + 4 - \sqrt 5 }}}} = \frac{{{a^2}}}{a} = a\)
Mục 3 trong SGK Toán 11 tập 2 thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, trước tiên chúng ta cần nắm vững lý thuyết và các công thức liên quan. Giaitoan.edu.vn sẽ cung cấp một bản tóm tắt lý thuyết cần thiết trước khi đi vào giải bài tập chi tiết.
Mục 3 trang 5, 6 thường bao gồm các dạng bài tập khác nhau, đòi hỏi học sinh phải vận dụng kiến thức đã học để giải quyết. Dưới đây là phân tích chi tiết từng bài tập:
Bài tập này yêu cầu học sinh… (Giải thích chi tiết yêu cầu bài tập và cung cấp lời giải chi tiết, kèm theo các bước thực hiện rõ ràng). Ví dụ, nếu bài tập yêu cầu tính giới hạn của một hàm số, cần trình bày các bước áp dụng quy tắc tính giới hạn, biến đổi đại số và kết luận.
Bài tập này tập trung vào… (Giải thích chi tiết yêu cầu bài tập và cung cấp lời giải chi tiết, kèm theo các bước thực hiện rõ ràng). Có thể bài tập này yêu cầu chứng minh một đẳng thức lượng giác, cần sử dụng các công thức lượng giác cơ bản và các phép biến đổi tương đương.
Bài tập này liên quan đến… (Giải thích chi tiết yêu cầu bài tập và cung cấp lời giải chi tiết, kèm theo các bước thực hiện rõ ràng). Ví dụ, bài tập có thể yêu cầu giải phương trình lượng giác, cần sử dụng các phương pháp giải phương trình lượng giác cơ bản và kiểm tra điều kiện của nghiệm.
Bài tập này đòi hỏi học sinh… (Giải thích chi tiết yêu cầu bài tập và cung cấp lời giải chi tiết, kèm theo các bước thực hiện rõ ràng). Có thể bài tập này yêu cầu tìm tập xác định của một hàm số, cần xác định các giá trị của x làm mẫu số bằng 0 hoặc biểu thức dưới dấu căn âm.
Để giúp các em hiểu rõ hơn về cách giải bài tập trong mục 3, chúng ta sẽ xem xét một ví dụ minh họa:
Ví dụ: Giải phương trình lượng giác: sin(x) = 1/2
Lời giải:
Hy vọng rằng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em đã có thể tự tin giải các bài tập trong mục 3 trang 5, 6 SGK Toán 11 tập 2. Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!