Bài 8.46 trang 90 SGK Toán 11 tập 2 thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến đường thẳng và mặt phẳng trong không gian. Bài tập này đòi hỏi học sinh phải nắm vững kiến thức về vectơ, phương trình đường thẳng và mặt phẳng.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập. Chúng tôi luôn cập nhật đáp án chính xác và nhanh chóng.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, AC = a, BC = \(\sqrt 2 \)a, SA vuông góc với mặt phẳng đáy và SA = a.
Đề bài
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, AC = a, BC = \(\sqrt 2 \)a, SA vuông góc với mặt phẳng đáy và SA = a. Góc giữa đường thẳng SB và mặt phẳng đáy bằng
A. 600.
B. 900.
C. 300.
D. 450.
Phương pháp giải - Xem chi tiết
Góc giữa d và (P):
+ Tìm giao điểm O của d và (P).
+ Từ A bất kì trên d, kẻ đường thẳng AA’ vuông góc xuống (P).
+ Góc AOA’ là góc cần tìm.
Lời giải chi tiết
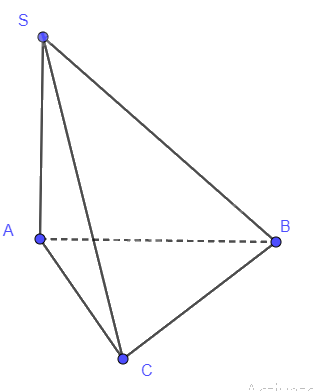
Góc giữa đường thẳng SB và mặt phẳng đáy là \(\widehat {SBA}\)
\(AB = \sqrt {A{C^2} + B{C^2}} = \sqrt {{a^2} + {{\left( {\sqrt 2 a} \right)}^2}} = \sqrt 3 a\)
\(\tan \widehat {SBA} = \frac{{SA}}{{AB}} = \frac{1}{{\sqrt 3 }} \Rightarrow \widehat {SBA} = {30^0}\)
Chọn đáp án C.
Bài 8.46 trang 90 SGK Toán 11 tập 2 yêu cầu giải một bài toán về vị trí tương đối giữa đường thẳng và mặt phẳng trong không gian. Để giải bài toán này, chúng ta cần nắm vững các kiến thức sau:
Phân tích bài toán:
Trước khi bắt đầu giải, cần đọc kỹ đề bài để xác định rõ các yếu tố đã cho: phương trình đường thẳng, phương trình mặt phẳng. Sau đó, xác định yêu cầu của bài toán: tìm giao điểm, chứng minh sự song song, vuông góc, hoặc tính khoảng cách.
Phương pháp giải:
Ví dụ minh họa (giả định bài toán cụ thể):
Giả sử bài toán yêu cầu tìm giao điểm của đường thẳng d: x = 1 + t, y = 2 - t, z = 3 + 2t và mặt phẳng (P): 2x - y + z - 5 = 0.
Thay phương trình đường thẳng vào phương trình mặt phẳng, ta được:
2(1 + t) - (2 - t) + (3 + 2t) - 5 = 0
2 + 2t - 2 + t + 3 + 2t - 5 = 0
5t - 2 = 0
t = 2/5
Thay t = 2/5 vào phương trình đường thẳng, ta được:
x = 1 + 2/5 = 7/5
y = 2 - 2/5 = 8/5
z = 3 + 2(2/5) = 3 + 4/5 = 19/5
Vậy giao điểm của đường thẳng d và mặt phẳng (P) là điểm I(7/5, 8/5, 19/5).
Lưu ý:
Tổng kết:
Bài 8.46 trang 90 SGK Toán 11 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về vị trí tương đối giữa đường thẳng và mặt phẳng trong không gian. Việc nắm vững phương pháp giải và luyện tập thường xuyên sẽ giúp học sinh tự tin giải quyết các bài toán tương tự.
Giaitoan.edu.vn hy vọng với lời giải chi tiết và dễ hiểu này, các em học sinh sẽ học tập tốt môn Toán 11 và đạt kết quả cao trong các kỳ thi.