Bài 4.4 trang 94 SGK Toán 11 tập 1 thuộc chương trình học về đường thẳng và mặt phẳng trong không gian. Bài tập này yêu cầu học sinh vận dụng kiến thức về vị trí tương đối giữa đường thẳng và mặt phẳng, các tính chất và định lý liên quan để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu cho Bài 4.4 trang 94, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
Trong mặt phẳng (P), cho tứ giác ABCD. Gọi S là điểm không thuộc mặt phẳng (P). Lấy M, N lần lượt là trung điểm của các đoạn thẳng SA, SC.
Đề bài
Trong mặt phẳng (P), cho tứ giác ABCD. Gọi S là điểm không thuộc mặt phẳng (P). Lấy M, N lần lượt là trung điểm của các đoạn thẳng SA, SC.
a) Xác định giao điểm K của đường thẳng SD và mặt phẳng (BMN).
b) Gọi P là giao điểm của hai đường thẳng MK và AD, Q là giao điểm của hai đường thẳng NK và CD. Chứng minh rằng ba diểm P, Q, B thằng hàng.
Phương pháp giải - Xem chi tiết
a) Tìm giao điểm của đường thẳng d và mặt phẳng (P)
Cách 1: Nếu (P) có chứa đường thẳng cắt d
\(\left\{ \begin{array}{l}a \subset \left( P \right)\\a \cap d = I\end{array} \right. \Rightarrow I = d \cap \left( P \right)\)
Cách 2: Nếu (P) không chứa đường thẳng cắt d
+ Bước 1: Tìm \(\left( Q \right) \supset d\) và \(\left( P \right) \cap \left( Q \right) = a\)
+ Bước 2: Tìm \(I = a \cap d \Rightarrow I = d \cap \left( P \right)\)
b) P, Q, B cùng thuộc 2 mặt phẳng phân biệt thì P, Q, B thẳng hàng.
Lời giải chi tiết
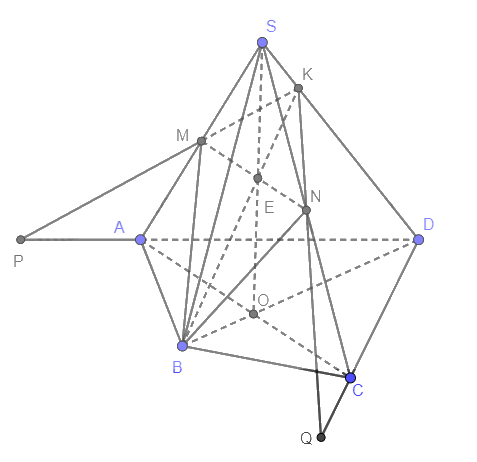
a) Trong (ABCD), gọi \(AC \cap BD = O\)
Trong (SAC), gọi \(SO \cap MN = E\)
\(\left\{ \begin{array}{l}BE \cap SD = K\\BE \subset \left( {BMN} \right)\end{array} \right. \Rightarrow K = SD \cap \left( {BMN} \right)\)
b) Theo phần a, K thuộc (BMN) nên mở rộng (BMN) thành (BMKN)
\(\begin{array}{l}\left\{ \begin{array}{l}MK \cap AD = P\\MK \subset \left( {BMNK} \right)\\AD \subset \left( {ABCD} \right)\end{array} \right. \Rightarrow P \in \left( {BMNK} \right) \cap \left( {ABCD} \right)\\\left\{ \begin{array}{l}NK \cap CD = Q\\NK \subset \left( {BMNK} \right)\\CD \subset \left( {ABCD} \right)\end{array} \right. \Rightarrow Q \in \left( {BMNK} \right) \cap \left( {ABCD} \right)\end{array}\)
\( \Rightarrow P,Q \in \left( {BMN} \right) \cap \left( {ABCD} \right)\)
Mà: \(B \in \left( {BMN} \right) \cap \left( {ABCD} \right)\)
Vậy P, B, Q thẳng hàng.
Bài 4.4 trang 94 SGK Toán 11 tập 1 là một bài tập quan trọng trong chương trình học về đường thẳng và mặt phẳng. Để giải quyết bài tập này, học sinh cần nắm vững các kiến thức cơ bản sau:
Trước khi bắt đầu giải bài tập, chúng ta cần phân tích đề bài để xác định rõ yêu cầu và các dữ kiện đã cho. Thông thường, bài toán sẽ cung cấp thông tin về vị trí của đường thẳng và mặt phẳng, các góc hoặc khoảng cách liên quan. Dựa vào đó, chúng ta có thể lựa chọn phương pháp giải phù hợp.
Để giải Bài 4.4 trang 94 SGK Toán 11 tập 1, chúng ta sẽ thực hiện các bước sau:
Ví dụ, nếu bài toán yêu cầu tính góc giữa đường thẳng và mặt phẳng, chúng ta có thể sử dụng công thức:
sin(α) = d(d, (P)) / AD
Trong đó:
Ngoài Bài 4.4 trang 94, SGK Toán 11 tập 1 còn có nhiều bài tập tương tự về đường thẳng và mặt phẳng. Các bài tập này thường yêu cầu học sinh:
Để giải các bài tập về đường thẳng và mặt phẳng một cách hiệu quả, học sinh nên:
Bài 4.4 trang 94 SGK Toán 11 tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về đường thẳng và mặt phẳng. Bằng cách nắm vững các kiến thức cơ bản, phân tích đề bài một cách cẩn thận và áp dụng các phương pháp giải phù hợp, học sinh có thể giải quyết bài tập này một cách hiệu quả. Giaitoan.edu.vn hy vọng rằng lời giải chi tiết và phân tích trên sẽ giúp các em học sinh hiểu rõ hơn về bài tập này và đạt kết quả tốt trong học tập.
| Khái niệm | Định nghĩa |
|---|---|
| Đường thẳng song song với mặt phẳng | Đường thẳng và mặt phẳng không có điểm chung. |
| Đường thẳng vuông góc với mặt phẳng | Đường thẳng tạo với mặt phẳng một góc 90 độ. |